一种快速找到等效最低点和等效最高点的方法

胡萍 孙建中

(句容市第三中学 江苏 句容 212400)

在高中物理教学中，“带电体在匀强电场中的圆周运动”是一类比较重要的题型，而解决这一类题目的关键是准确地找到等效最低点和等效最高点．下面笔者通过一道例题介绍一种简单易行的方法，供参考．

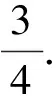
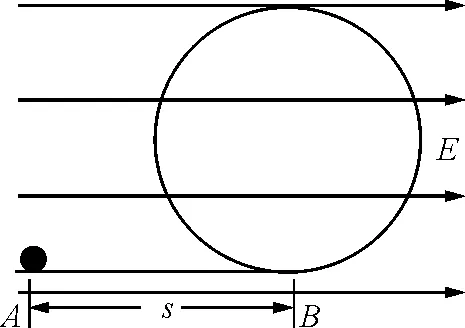
图1

解析：本题的关键是找到等效最高点，而这恰恰是学生解题时的一个难点.如何快速准确地找到等

效最低点和最高点？可以设想将带电小球移至圆心O处，在圆心O处对小球做受力分析(图2).利用平行四边形定则作电场力Eq与重力mg的合力F，再作与F重合的圆的直径MN,则M即为等效最低点，N为等效最高点.由题可知，带电小球能否做完整的圆周运动的临界条件是能否通过N点.若恰好能通过N点，即达到N点时小球与环之间的弹力恰好为零．

图2

在N点由圆周运动知识得

(1)

设合力F与重力mg之间的夹角为θ，则

小球从A点到N点由动能定理，有

(2)

联立(1)、(2)式并代入θ值，则可求出A,B之间的距离

总结:在等效场中，要快速准确地找到等效最低点和等效最高点，我们可以假设将带电体移到圆心处，在圆心处对带电体做受力分析，利用平行四边形定则得出合力，则与合力重合的圆的直径与圆的两个交点即为等效最低点和等效最高点．