可测集的一个充分必要条件

郑利凯

(内蒙古民族大学 数学学院,内蒙古 通辽 028000)

1 引言

判断Rn中的点集E是否可测是实变函数论学科研究的重要内容，也是实变函数其它理论的基础．本文以卡拉泰奥多里条件为基础，推导出Rn中的点集E是可测集的一个充要条件.

下面给出一些基本结论和引理．

定义1[1-2]设E为Rn中的点集,如果对于任一点集T⊂Rn,都有:m*T=m*(T∩E)+m*(T∩CE)(卡拉泰奥多里条件),则称E是L可测的或可测的,这时E的外测度m*E称为E的L测度,记为mE，其中m*T为T的L外测度.

引理1[1-2]设A⊂B,则m*A≤m*B.

引理3[4]设S1,S2都可测,则S1∪S2也可测,并且当S1∩S2=φ时,对于任意集合T总有m*[T∩(S1∪S2)]=m*(T∩S1)+m*(T∩S2).

引理4[5]S可测的充要条件是CS可测.

引理6[6]区间I都是可测集合,且mI=|I|.

引理7 设E是Rn中可测集,则∀ε>0,存在闭集F⊂E,使得m(E-F)<ε.

证明当mE<时,∀ε>0,存在一列开区间{Ii},i=1,2,…,使得⊃E,且令则G为开集,G⊃E,且因此mG-mE<ε,从而m(G-E)<ε.

当mE<时,E总可以表示为可数个互不相交的有界可测集的并集,即其中En=(Sn-Sn-1)∩E,Sn为球S(0,n),En为有界可测集.根据以上结论,对每个En,存在开集Gn,使得Gn⊃En且令则G为开集,G⊃⊂因此,(引理5)<ε.

当E可测时,CE也可测,所以对任意ε>0,存在开集G,G⊃CE,且m(G-CE)<ε.又因为G-CE=G∩E=E∩C(CG)=E-CG,令F=CG,则F是闭集且F⊂E,m(E-F)=m(G-CE)<ε.

2 Rn中可测集的一个充要条件

根据以上引理,可以得出Rn中的点集可测的一个充要条件.

定理1 点集E⊂Rn为可测集的充要条件是:∀正数ε>0,∃闭集F1和F2,使得F1⊂E,F2⊂CE,且m(Rn(F1∪F2))<ε.

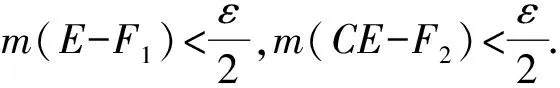
充分性 若Rn中的点集E满足:∀正数ε>0,∃闭集F1和F2,使得：F1⊂E,F2⊂CE,且m(Rn(F1∪F2))<ε.Rn(F1∪F2)=Rn∩C(F1∪F2)=Rn∩CF1∩CF2,由m(Rn(F1∪F2))<ε,可得:Rn∩CF1∩CF2<ε.任意点集T⊂Rn,因为F1⊂E,所以CE⊂CF1,T∩CE⊂T∩CF1.根据引理1有m*(T∩CE)≤m*(T∩CF1).同理,m*(T∩E)≤m*(T∩CF2).m*(T∩E)+m*(T∩CE)≤m*(T∩CF1)+m*(T∩CF2)=m*(T∩CF1∩(F2∪CF2))+m*(T∩CF2).因为F2∩CF2=φ,根据引理3有:m*(T∩CF1∩(F2∪CF2))=m*(T∩CF1∩F2)+m*(T∩CF1∩CF2).所以m*(T∩E)+m*(T∩CE)≤m*(T∩CF1∩F2)+m*(T∩CF1∩CF2)+m*(T∩CF2)≤m*(T∩F2)+ε+m*(T∩CF2)因为F2∩CF2=φ,根据引理3有:m*(T∩F2)+m*(T∩CF2)=m*(T∩(F2∪CF2))=m*(T∩Rn)=m*T.所以有:m*(T∩E)+m*(T∩CE)≤m*T+ε.由ε的任意性,可得m*(T∩E)+m*(T∩CE)≤m*T.又T=T∩Rn=T∩(E∪CE)=(T∩E)∪(T∩CE),由引理2可得:m*T=m*((T∩E)∪(T∩CE))≤m*(T∩E)+m*(T∩CE),所以有:m*T=m*(T∩E)+m*(T∩CE).根据定义1可知:点集E是Rn中的可测集.

3 可测集的充分必要条件的应用

下面应用这个充分必要条件,证明Cantor集为可测集.

例1 证明Cantor集P为可测集.

证明因为Cantor集P是闭区间[0,1]去掉可数个互不相交的开区间得到的点集,所以由点集P的做法可知,Cantor集P是没有内点的完备集,疏朗的完备集.下面以定理1证明Cantor集P是可测集.

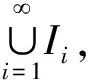
又因为Cantor集P是完备集,所以可以取闭集F1=P,则F1⊂P,m(P-F1)=0.因为Rn(F1∪F2)=(P∪CP)(F1∪F2)=(P(F1∪F2))∪(CP(F1∪F2))⊂(P-F1)∪(CP-F2),所以m(Rn(F1∪F2))≤m((P-F1)∪(CP-F2))≤m(P-F1)+m(CP-F2)<0+ε=ε.

根据定理1可知Cantor集P是可测集.

利用这个充要条件,类似例1可以容易地证明Rn中的一切完备疏朗集都是可测集.可见,定理1为判断Rn中的点集是不是可测集提供了很大方便.

[1] 程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].2版.北京:高等教育出版社,2003:54-70.

[2] 周民强.实变函数论[M].北京:北京大学出版社,2001:79-90.

[3] 覃崇文.可测集定义的一个附注[J].重庆文理学院学报:自然科学版,2007，6(4):17-18.

[4] 胡冰,周其生.关于可测集用疏朗完备集逼近问题[J].重庆工商大学学报:自然科学版,2006,23(6):540-541.

[5] 戴培良.可测集合的结构[J].常熟理工学院学报，2005,19(2):6-10.

[6] 吴振之.可测集合的几个等价定义[J].江汉大学学报,1996(3):83-85.