广义函数空间上Quadratic函数方程的Hyers－Ulam－Rassias型稳定性

李林松，朴青松

（延边大学理学院 数学系，吉林 延吉133002）

广义函数空间上Quadratic函数方程的Hyers－Ulam－Rassias型稳定性

李林松，朴青松

（延边大学理学院 数学系，吉林 延吉133002）

利用热方程的核，通过对广义函数正则化的方法，给出了在广义函数空间上二次函数方程的改进的Hyers－Ulam－Rassias型稳定性定理，从而推广了文献［8］的结果.

热方程的核；广义函数；quadratic函数方程；稳定性

函数方程的稳定性研究是近年来比较活跃的研究领域，并且取得了大量的研究成果［1－5］.最近，J.Chung等从另一个角度在广义函数空间上讨论了函数方程的稳定性，取得一些重要的研究成果［6－10］.本文根据上述文献提供的方法，在广义函数空间上讨论了二次函数方程的改进的Hyers－Ulam－Rassias型函数方程稳定性：

其中δ≥0，ψp（x）为非负连续p阶齐次函数，0＜p＜2.文献［3］讨论了不等式（1）的右边是常数的情况，而本文将常数用齐次函数来代替，因而进一步推广了文献［8］的结论.

1 基本概念和引理

首先给出几个记号：x＝ （x1，…，xn）∈Rn，α＝ （α1，…，αn）∈Nn0，xα＝xα11…xαnn，∂α＝∂α11…∂αnn，∂j＝∂／∂xj，其中N0表示非负整数集.

定义［12－13］若Rn上的无穷可微函数φ，对 ∀α，β∈Nn0，满足不等式

则称φ（x）为速降函数.速降函数全体构成的线性空间记为S（Rn）或者S，由拟范数族使S成为Frechet空间．我们将基本函数空间S上的连续线性泛函全体构成的线性空间记作S′（Rn）或S′，即S′为S的对偶空间，S′中的元素称为缓增广义函数．由于f为广义函数时，不等式（1）没有意义，因此我们首先将不等式（1）在广义函数空间上重新定义．设A，B，P1，P2分别为：A（x，y）＝x＋y，B（x，y）＝x－y，P1（x，y）＝x，P2（x，y）＝y，x，y∈Rn，则不等式（1）可重新描述为

其中uoA，uoB，uoP1和uoP2分别为广义函数u∈S′关于函数A，B，P1和P2的拉回（pullback），则规定为：事实上，对于uoA，uoB，uoP1，uoP2有下列运算［12］：

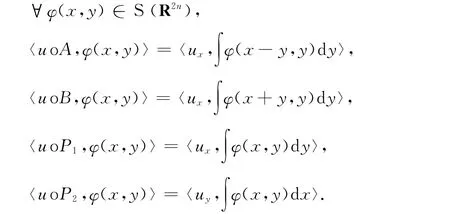
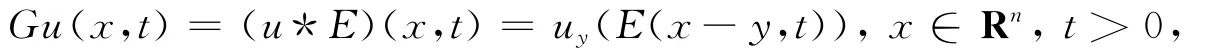
并称其为广义函数u的高斯变换［12－14］．事实上，u的高斯变换Gu（x，t）∈C∞（Rn×R＋），且当t→0＋时，Gu（x，t）→u（S′）．即，对于任意φ∈S（Rn），有

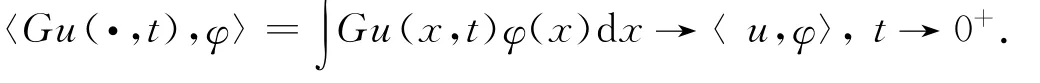
引理1 设fυ（x）是Rn上的函数列，满足下列条件，则fυ在S′中收敛于零．

1）fυ（x）在Rn的任意紧子集上一致收敛于零；

2）存在常数C＞0，k＞0使得对所有的υ∈N，有

证明 由1）对任意ε＞0及X＞0，存在N∈N；∀υ＞N及有另外，由于φ（x）∈S，对任意h＞0存在C1＞0，有．因此，当υ＞N，并取h和X充分大时，有

引理2 设ψp（x）是非负连续p阶齐次函数，其中0＜p＜2．若Ψp（x，t）＝ （ψp＊Et）（x）＝则对任意t＞0，级数在S′中收敛．

证明 首先证明对每个t＞0，级数在Rn的任意紧子集上一致收敛．为此我们只需证明对每个t＞0，Ψp（x，t／2j）在任意紧集上关于j∈N一致有界．即，对于每个t＞0及Rn的每个紧子集，存在与j∈N无关的常数C＞0，使得Ψp（x，t／2j）≤C．显然，∫RnE（y，t／2j）dy＝1，并且对t＞0，δ＞0，h≥0，当j→∞ 时，．设，则由ψp（x）连续性和齐次性有因此

其中M1与j无关.故级数在任意紧集上一致收敛.再由式（3）及引理1，引理2得证.

引理3 设δ＞0，ψp（x）如引理2所定义，Ψp（x，t）＝ （ψp＊Et）（x）.若f∶Rn×（0，∞）→C是连续函数，且满足不等式

则存在唯一的函数g（x，t），使得

并且

其中K是只与p有关的常数.

证明 定义算子T：Tf（x，y，t，s）＝f（x＋y，t＋s）＋f（x－y，t＋s）－2f（x，t）－2f（y，s），并设F（x，t）＝f（x，t）－f（0，t），则由式（4）有

在（7）式中，令x＝y，t＝s，两边再除4可得

依此类推，并由三角不等式可得

容易证明，对于r＞0，Ψp（rx，r2t）＝rpΨp（x，t）.故对上面不等式的右边做计算，得

其中K1是只与p有关的常数.

同理，在（4）式中，令x＝y＝0，t＝s，两边再除2可得

其中K2是只与p有关的常数.现令

其中C3＝Ψp（x，t／2n）＋Ψp（y，s／2n）＋Ψp（0，t／2n）＋Ψp（0，s／2n），C4＝Ψp（0，t）＋Ψp（0，s）.由于limt→0Ψp（x，t）＝ψp（x），因此令n→ ∞ 即得到（5）式.由（8）、（9）、（10）式可得

其中K＝K1＋K2.再令n→∞，即得到（6）式.

现在我们考虑g（x，t）的唯一性.设G（x，t）＝g（x，t）－g（0，t），由文献［8］知，对任意有理数r，有G（rx，t）＝r2G（x，t）.现假设h（x，t）也满足（5）和（6）式，并且令H（x，t）＝h（x，t）－h（0，t），则由（6式及三角不等式可得

2 主要结果

定理1 设δ≥0，ψp（x）如引理2所定义.若u∈S′（Rn）满足不等式

证明 对不等式（11）用热方程的核的张量积Et（x）Es（y）做卷积，则由文献［7，8，10］的方法可得到

其中Gu（x，t）是u的高斯变换，Ψp（x，t）＝ （ψp＊Et）（x）.由引理3知，存在唯一的函数g（x，t），使得g（x＋y，t＋s）＋g（x－y，t＋s）－2g（x，t）－2g（y，s）＝0，并且

因为高斯变换Gu（x，t）是无穷可微函数，所以由引理3的证明过程可知g（x，t）必为连续函数，因此由文献［11］有对不等式（12），令t→0＋，则由引理2可知，其中证毕.

［1］Czerwik S.On the Stability of the Quadratic Mapping in Normed Spaces［J］.Abh Math Sem Univ Hamburg，1992，62：59－64.

［2］Rassias T M.On the Stability of the Functional Equations in Banach Spaces［J］.J Math Anal Appl，2000，250：264－284.

［3］Chang I S，Kim H M.Hyers－Ulam－Rassias Stability of a Quadratic Functional Equation［J］.Kyungpook Math J，2002，42：71－86.

［4］Czerwik S，Dlutek K.Stability of the Quadratic Functional Equation in Lipschitz Spaces［J］.J Math Anal Appl，2004，293：79－88.

［5］Fechner W.On the Hyers－Ulam Stability of Functional Equations Connected with Additive and Quadratic Mappings［J］.J Math Anal Appl，2006，322：774－786.

［6］Baker J A.Distributional Methods for Functional Equations［J］.Aeq Math，2001，62：136－142.

［7］Chung J，Chung S Y，Kim D.The Stability of Cauchy Equations in the Space of Schwartz Distributions［J］.J Math Anal Appl，2004，295：107－114.

［8］Chung J.Stability of Functional Equations in the Space of Distributions and Hyperfunctions［J］.J Math Anal Appl，2003，286：177－186.

［9］Chung S Y.Reformulation of Some Functional Equations in the Space of Gevrey Distributions and Regularity of Solutions［J］.Aeq Math，2000，59：108－123.

［10］Li L，Chung J，Kim D.Stability of Jensen Equations in the Space of Generalized Functions［J］.J Math Anal Appl，2004，299：578－586.

［11］Chung J，Lee S Y.Some Functional Equations in the Spaces of Generalized Functions［J］.Aeq Math，2003，65：267－279.

［12］H¨ormander L.The Analysis of Linear Partial Differential Operator I［M］.Berlin，Ne wYork：Springer－Verlag，1983.

［13］Schwartz L.Théorie Des Distributions［M］.Paris：Hermann，1966.

［14］Matsuzawa T.A Calculus Approach to HyperfunctionsⅢ［J］.Nagoya Math J，1990，118：133－153.

Hyers－Ulam－Rassias Stability of Quadratic Functional Equation in Distributions

LI Lin－song，PIAO Qing－song
（DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China）

Making use of heat kernel and the method of regularizing generalized functions we prove the Hyers－Ulam－Rassias stability of quadratic functional equation in distributions，which generalized the result of［8］.

heat kernel；distributions；quadratic functional equation；stability

O178；O177.4

A

1004－4353（2011）03－0189－05

2011－05－21

教育部回国留学基金资助项目（教外司留［2008］第890号）

李林松（1968—），男，博士，副教授，研究方向为应用泛函分析.