第二类q-Beta算子的逼近性质
蔡清波
(泉州师范学院 数学与计算机科学学院,福建 泉州362000)
第二类q-Beta算子的逼近性质
蔡清波
(泉州师范学院 数学与计算机科学学院,福建 泉州362000)
基于q-积分的概念,研究了第二类q-Beta算子的逼近性质.通过计算得到了算子的各阶矩量及中心距量,并由光滑模和k-泛函分析得到算子的局部逼近性质.由于当q→1-时,算子退化到经典的第二类Beta算子,故其是对第二类Beta算子收敛性质的一种推广.
q-积分;q-Beta算子;矩;收敛阶
0 引言
近年来,q-整数在逼近论中的应用成为该领域的一个研究热点.自1997年Phillips在文[1]中提出q-Bernstein算子以来,很多学者对相关问题进行了研究,并得到了许多重要的结论[1-4].
首先,引入与q-整数及q-微积分的相关一些概念[5-6].对任意固定的实数q>0及非负整数k,定义q-整数为更一般地,对于非整数t,定义分别定义q-阶乘及q-二项系数为和定义无穷限q-积分为假设级数绝对收敛.此外,定义如下函数q-Gamma积分定义为且满足Γq(t+1)= [t]qΓq(t),Γq(1)=1.
定义第二类q-Beta函数为

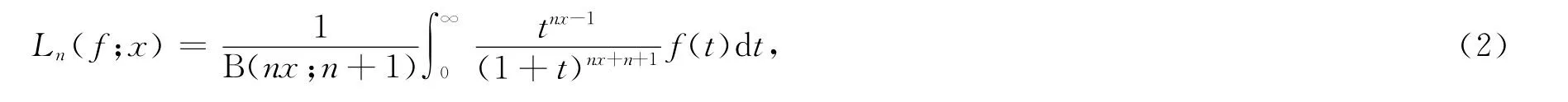
其中算子Ln(f;x)是由Stancu定义的正线性算子,在区间(0,∞)上是局部可积函数,当t→∞,n→∞时是以多项式阶增长的[7].在此基础上,定义第二类q-Beta算子.设f∈C[0,∞),q∈ (0,1),则

值得注意的是,若q→1-,则Ln,1-(f;x)即为式(2)所定义的算子.
2 引理及证明
引理1 设f∈C[0,∞),q∈ (0,1),则如下等式成立:

证明 由q-Beta函数的定义(1),易得故(4)式成立.此外由于K(x;t+1)=qtK(x;t)[4],从 而 有又因从而故(5)式成立.最后,由于故(6)式成立,引理1得证.
注1 由引理1,当q→1-时,Ln,1-(1;x)=1,Ln,1-(t;x)=x和为第二类Beta算子的各阶矩量[8].
引理2 设f∈C[0,∞),q∈ (0,1),则有
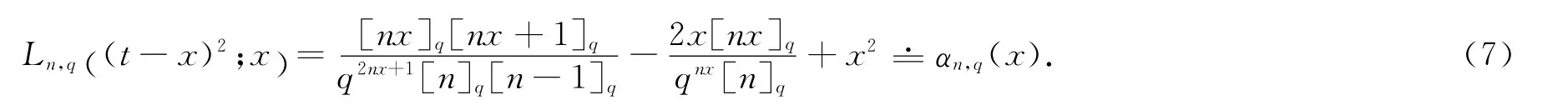
证明 由Ln,q(t-x)2;(x=Ln,q(t2;x)-2xLn,q(t;x)+x2及引理1易得证.)
注2 由引理2,当q→1-时为第二类Beta算子的二阶中心距量[8].
3 主要结论
令CB[0,∞)为定义在[0,∞)上的实值连续有界函数空间,定义范数为k-泛函定义为其中δ>0,由文献[9]中的定理2.4知,存在常数C>0,使得

定理1 设f∈CB[0,∞),q∈ (0,1),则存在常数C>0,使得对x∈ [0,∞)有

其中αn,q(x)如(7)式所定义.
证明 构造辅助算子
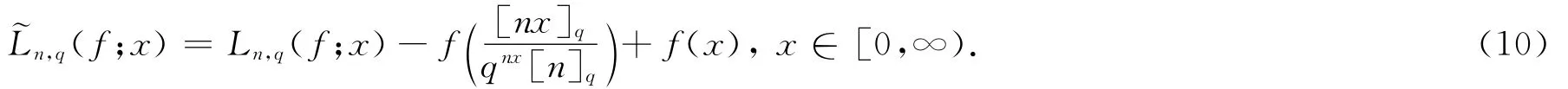

令g∈C2B,由Taylor展开及(11)式,有从而,由(10)式及引理2,有

其中δn,q(x)如(7)式所定义.又由(10)和(3)式及引理1,有

从而由(10)和(12)式可得

在上述不等式右端中,对g∈W2取下确界有
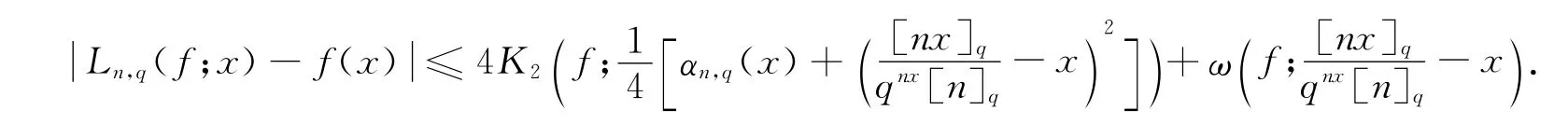
注3 令q={qn}为满足0<qn<1的序列,则有及从而得到算子Ln,qn(f;x)收敛到f(x)的点态收敛阶.
考虑如下函数类:设Hx2[0,∞)为定义在[0,∞)上且满足条件的函数f的集合,其中Mf为只依赖于f的常数.记Cx2[0,∞)为包含于Hx2[0,∞)的所有连续函数子空间.定义f在闭 区间[0,a],a>0上的光滑模为
定理2 设f∈Cx2[0,∞),q∈ (0,1),ωa+1(f;δ)为有限区间[0,a+1]⊂ [0,∞),a>0上的光滑模,则有其中αn,q(a)如(7)式所定义.
证明 当x∈ [0,a],t>a+1,由t-x>1有

当x∈ [0,a],t≤a+1时,有

由(13)和 (14)式 可 得,当x∈ [0,a],t≥ 0 时 有从而所以,由Schwartz不等式及引理2知,当q∈(0,1),x∈ [0,a]时,有取定理2得证.
[1]Phillips G M.Bernstein Polynomials Based on theq-integers[J].Ann Numer Math,1997,4:511-518.
[2]Mahmudov N I.Statistical Approximation of Baskakov and Baskakov-Kantorovich Operators Based on theq-integers[J].Cent Eur J Math,2010,8(4):816-826.
[3]Do~gru O,Duman O.Statistical Approximation of Meyer-K¨onig and Zeller Operators Based onq-integers[J].Publicationes Mathematicae Debrecen,2006,68(1/2):199-214.
[4]De Sole A,Kac V G.On Integral Representation ofq-gamma andq-beta Functions[J].Atti Accad Naz Lincei Cl Sci Fis Mat Natur Rend Lincei(9)Mat Appl,2005,16:11-29.
[5]Gasper G,Rahman M.Basic Hypergeometric Series,Encyclopedia of Mathematics and its applications[M].UK Cambridge:Cambridge University Press,1990:35.
[6]Kac V G,Cheung P.Quantum Calculus[M].Ne wYork:Universitext,Springer-Verlag,2002.
[7]Stancu D D.On the Beta Approximation Operators of Second Kind[J].Rev Anal Numér Théor Approx,1995,24:231-239.
[8]Abel U.Asymptotic Approximation with Stancu Beta Operators[J].Rev Anal Numér Théor Approx,1998,27:5-13.
[9]DeVore R A,Lorentz G G.Constructive Approximation[M].Berlin:Springer,1993.
Approximation Properties of the Second Kindq-Beta Operators
CAI Qing-bo
(SchoolofMathematicsandComputerScience,QuanzhouNormalUniversity,Quanzhou362000,China)
We introduced the second kind of Beta operators based on the concept ofq-integral.We computed the moments and central moment of the operators,and investigated local approximation properties by the modulus of continuity andk-functional with analysis techniques.
q-integral;q-Beta operators;rate of convergence;moments
O174.41
A
1004-4353(2011)03-0208-04
2011 -05 -07
福建省教育厅科技项目(JK2011041)
蔡清波(1981—),男,讲师,研究方向为算子逼近论及计算几何.

