具有指定Julia方向的有限级整函数
南 华
(延边大学理学院 数学系,吉林 延吉133002)
具有指定Julia方向的有限级整函数
南 华
(延边大学理学院 数学系,吉林 延吉133002)
根据整函数的Julia方向的定义,研究了整函数的Julia方向问题.构造了以指定方向为Julia方向的有限级整函数f(z),同时还构造了具有指定Julia方向和指定Julia例外点的整函数.
Julia方向;整函数的级;Julia例外值
0 引言
整函数和亚纯函数的值分布一直受到学者们的关注,并且取得了许多重要的成果[1-3].在值分布理论的发展过程中,著名数学家E.Picard和G.Julia获得了很多突出的成果,其中包括著名的Picard定理[4]和Julia定理[1].Picard定理说明了在本性奇点的一个邻域内函数的A-点集的分布情况,而Julia定理断言对任意给定的有限复数A(除一点外),函数在一条射线附近有无穷多的A-点,这条射线便是Julia方向.Julia方向可能有几条或者可能有无数条.
例 考察函数f(z)=ez,它有2个Julia方向,即正虚轴和负虚轴.
事实上,对于每一个复数z0(z0≠0),方程ez=z0的解具有如下形式:
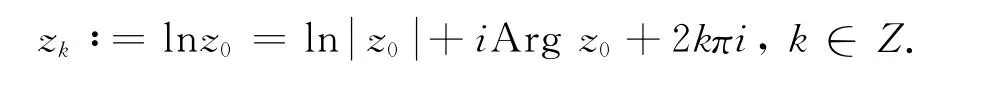
如果k是正整数,则连接原点和zk的线段与正虚轴的夹角的正切值等于.显然当k→∞时,这个正切值趋近于0.这意味着对于每一个复数z0(z0≠0),在任意包含正虚轴的角域内,函数ez取z0值无穷多次.对于负整数k和负虚轴也有类似结论,因而函数f(z)有2个Julia方向.对每种情形而言,Julia例外点是原点.另外,由公式函数的级可得f(z)的级是1.
近几年,对函数的Julia方向的研究有很多,如Jin Lu[5]研究了具有小级数的整函数的Julia方向,M.V.Zabolots′kyi[6]研究了缓慢增长的整函数的Julia方向,但这些都是对满足一定条件的整函数的Julia方向的存在性及其性质的研究,仅给出了Julia方向存在的必要性.本文将构造一个具有有限级的整函数,并使其具有指定的Julia方向.本文结果不仅说明了这种整函数的存在性,而且还提供了一种构造这类整函数的方法.
1 引理及其证明
引理1[7]给定一非负整数λ和单调递增趋近于无穷大的非零序列{ξn}.τ≠∞是序列{ξn}的收敛
指数,κ是使级数发散的非负整数k的最大值 若函数

其中Q(z)是v次多项式,且当κ=0时指数项消失,则函数f(z)是具有有限级ρ=max(υ,τ)的整函数,它的所有零点为
由此引理可知,当序列{ξn}以充分快的速度趋近于0时,函数f(z)表达式中的指数项可以去掉.
证明 由于数列{an}充分快速地趋近于∞,因而我们不妨设对所有的j=1,2,3,… 都成立.在每个紧集Cj(j=1,2,3,…)中,整函数f(z)都可以在某一点取得最小值.固定j,令
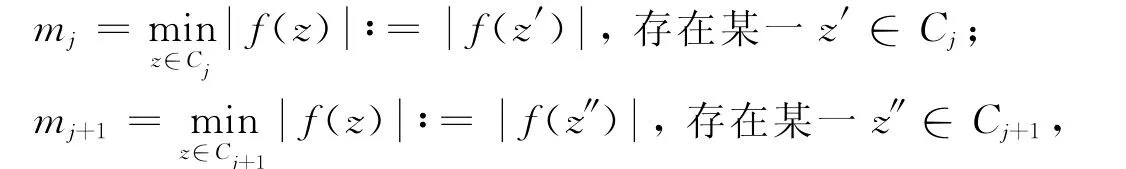
设M>0.由于j→∞时有mj→∞,所以必存在自然数N,使得j≥N时有M.令对任意的满足时,必存在一整数n使得.又由于是紧的,函数在K内某点处取得最小值.另外,在K内f(z)不为0,因此由最小模原理有在Bd(K)的某点处取得最小值.
2 主要结果
定理 设θ0是一实数(mod 2π),则必存在仅以χ(θ0)为Julia方向的有限级整函数f(z).
证明 设复数列{an}满足:①,且以足够快的速度趋于∞使得∞;②argaj=θ0,j=1,2,3,….令函数f(z)和点集Cj、Dj及mj与本文引理2中所设相同.由于j→∞时mj→∞,因此对于任意的复数z0都存在自然数N>0,使得j≥N时对一切的z∈Cj都成立.
于是对所有的z∈Cj和j≥N有.再根据Rouche’s定理可知,函数f(z)-z0与f(z)在Cj内部有相同个数的零点,而对Cj的内部的点aj有f(aj)=0.这说明在Dj(j≥N)内f(z)=z0有解.由z0点的任意性知,在集合的内部f(z)可取得任意复数值无穷次.设角域Sδ={z∶θ0-δ<argz<θ0+δ},δ>0.显然对充分大的j有Dj⊂Sδ,因此θ0是函数f(z)的Julia方向.对任意的θ≠θ0(0≤θ≤2π),设角域S′δ={z∶θ-δ<argz<θ+δ},δ>0.由引理2可知,对所有的z∈S′δ,当z→∞ 时有f(z)→∞.因此χ(θ0)是整函数f(z)唯一的Julia方向.另外,根据性质① 可知{an}的收敛指数再由引理1可知,函数f(z)的级是有限的.定理证毕.
推论 给定实数θ0(mod 2π)和任意复数z0,必存在1个整函数F(z),使得χ(θ0)是函数F(z)的Julia方向,而z0是Julia例外值.
证明 令F(z)=z0+p(z)ef(z),其中f(z)与定理中的函数f(z)相同,而p(z)是次数为λ的非常值多项式,那么显然F(z)取得z0值只能是有限次(λ次).
由上面的定理得知,f(z)在集合∪∞j=1Dj中取得任意复数值无穷多次.因此函数ef(z)在集合 ∪∞j=1Dj中
除了0之外取得其他任意复数值无穷多次.所以函数F(z)取z0值有限多次,取其他任意复数无穷多次.设Sδ= {z∶θ0-δ<argz<θ0+δ},δ>0.对充分大的j有Dj⊂Sδ,因此χ(θ0)是整函数F(z)的Julia方向,且z0是Julia例外值.
[1]Julia G.Lecons Sur Les Fonctions a Point Singulier Essentiel Isole[M].Paris:Imprimerie Gauthier-Villa,1924.
[2]Tu Z H.On the Julia Directions of the Value Distribution of Holomorphic Curves onPn(C)[J].Kodai Math J,1996,19:1-6.
[3]南华.超越整函数的正规族{f(2nz)}[J].延边大学学报:自然科学版,2010,36(2):109-113.
[4]Dieter Gaier.Lectures on Complex Approximation[M].Boston:Birkhäuser,1987.
[5]Jin Lu.On Julia Directions of Entire Functions of Small Order[J].KODAI Math J,2002,25:72-78.
[6]Zabolots′kyi MV.Julia Lines of Entire Functions of Slo wGrowth[J].Ukrainian Mathematical Journal,2006,58:937-944.
[7]Markushevich A I.Theory and Functions of a Complex Variable:Vol.II[M].Ne wYork:Chelsea Publ Co,1977:251-258.
An Entire Function of Finite Order with Preassigned Julia-line
NAN Hua
(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)
We studied the Julia direction of an entire function.An entire functionf(z)which has the preassigned Julia-line was construted,and the order of the entire functionf(z)was discussed.Moreover,we constructed an entire function which has the preassigned Julia-line and Julia exceptional value.
Julia-line;order of entire function;Julia exceptional value
O174.5
A
1004-4353(2011)03-0223-03
2011 -05 -17
延边大学科研项目(延大科合字[2010]第002号)
*通信作者:南华(1972—),女,博士,副教授,研究方向为复变函数.

