＊ 基于小波包分解的细胞膜离子电流重构

乔晓刚,吴晋芝,乔晓艳

(1.山西青年管理干部学院计算机系,山西太原 030001;2.山西大学物理电子工程学院,山西太原 030006)

＊基于小波包分解的细胞膜离子电流重构

乔晓刚1,吴晋芝2,乔晓艳2

(1.山西青年管理干部学院计算机系,山西太原 030001;2.山西大学物理电子工程学院,山西太原 030006)

提出了一种基于小波包算法重构离子电流信号的新方法,利用小波包分解对离子电流进行多分辨率分析,获得尺度能量分布特征信号.然后,进行小波包重构,再经过平滑滤波,恢复通道离子电流信号.仿真实验结果表明,采用小波包算法,在较低信噪比时,离子电流恢复精度高,算法收敛速度快,且具有较强的抗噪能力.

离子单通道电流;小波包分解;尺度能量分布;信号重构

离子通道是镶嵌在可兴奋细胞膜内的跨膜蛋白质大分子,其间有离子选择性孔道,某些构象下孔道开放,允许某种或几种离子沿电化学梯度流过,形成皮安(pA)级离子电流,膜片钳技术可以记录到离子电流信号.在膜片钳测量系统中,通常采用阈值检测方法消除噪声,由于该方法不仅需要人为设定阈值,并且在信噪比较低(SNR＜5.0)时,电流恢复误差不能满足膜片钳测量系统的精度要求.基于隐马尔可夫模型(HMM)的离子单通道电流恢复是在强噪声背景下,从膜片钳记录中得到理想化通道电流的一种有效方法[1].然而,HMM算法中的状态重估公式只有在确知通道状态数目的条件下才能应用,在强背景噪声下,这一先验知识往往很难获得,并且 HMM算法计算过程繁琐,计算量较大,很难适用于实时处理系统[2-3].由于小波算法具有良好的时频局部化分析特性,近年来被广泛应用于非平稳信号的实时处理中[4].但是,随着小波分解尺度的增大,正交小波基函数的时间分辨率愈高,其频率分辨率愈低[5].小波包分解可以弥补小波算法的这一缺陷,它不仅对信号低频部分进行分解,对没有细分的高频部分也进行了再分解,充分利用了正交多分辨率分析的思想[6].本文利用小波包变换对强噪声污染的离子电流信号进行精细的多分辨分析和重构,与小波变换方法相比,有效地提高了信号恢复精度,同时该方法可以应用于实时处理系统中.

1 小波包基本理论

小波包分解能够为信号提供一种更加精细的分析方法,通过把频带进行多层次划分,对多分辨率分析中没有细分的高频部分进一步分解,并能够根据被分析信号的特征,自适应地选择相应频段,使之与信号频谱相匹配,从而提高时频分辨率.

在多分辨率分析中,定义子空间是函数un(t)的闭包空间,而是函数u2n(t)的闭包空间,并令满足双尺度方程:

式中g(k)=(-1)k h(1-k)为正交滤波器系数.当n=0时,u0(t)=φ(t)为尺度函数;u1(t)=ψ(t)为小波函数.由式(1)构造的序列{un(t),n∈Z+}称为正交尺度函数φ(t)确定的正交小波包[7].

基于小波包变换的分析技术主要包括小波包分解和小波包重构两部分.设原始信号f(n),则小波包分解算法为:

式中j=1,2,…,J为分解层数,i=1,2,…,2j;dij表示第j层上第i个小波包分解系数,h和g分别是正交镜像低通分解滤波器和高通分解滤波器.

小波包重构算法是其分解算法的逆过程,重构公式为:

式中j=J-1,J-2,…,1,0为重构层数,i=2j,2j-1,…,2,1表示第j层上的第i个小波包重构系数,h′和g′分别是正交镜像的低通重构滤波器和高通重构滤波器.小波包分解与重构的结构图如图1所示.

图1 小波包分解和重构结构图Fig.1 Diagram of wavelet package decomposing and reconstructing

2 基于小波包的离子电流信号重构

细胞膜离子单通道电流具有定量特性,表现出全有和全无的特征,为一个个电流幅值恒定,持续时间宽度随机变化的矩形波.虽然从单通道电流记录看,离子通道只存在开放与关闭持续时间两种现象,但是通道门控动力学不只有开放、关闭两种状态,而是存在平均持续时间不同的多个开放和多个关闭状态,而各个开放或关闭状态表现出相同的外在电流水平,称构象的聚合特性[8].状态间按照某种方式连接且相互转移,这种状态间的相互转移服从一个时间连续、状态有限的一阶Markov过程[1].

Harr小波函数具有和单通道电流相似的形状,并且 Harr小波是一个具有紧支撑的正交小波函数,因此本文选用 Harr小波作为分析小波.小波包算法实现过程描述如下:

(1)小波包分解

设离子单通道电流信号为f(n),频率范围(0～512 Hz),对其进行四层小波包分解,分解信号为f40(0～32 Hz),f41(32～64 Hz),…,f415(480～512 Hz),所对应频段分别为1-16.提取第四层各频带范围的信号,即第四层的小波包分解系数,则有f=f40+f41+…+f415,其中f4k(k=0,1,2,…,2j-1)表示第四层各频段的分解信号.

(2)尺度能量分布

对于一个能量有限的信号f(n)(n=1,2,…,N),其总能量为:

对信号进行j层分解,所得各频段的能量表示为:

其中,j为分解层数,fj,k(n)为小波包分解各频段信号.

(3)重构离子单通道电流

从尺度能量分布图上,选择尺度能量较高的小波包分解系数,所对应频段包含了信号的特征,对这些频段的分解系数进行小波包重构,其它频段的分解系数则认为包含了大量的背景噪声信号,重构时置为0.最后,求出重构后各频段信号的矢量和,经过低通滤波平滑处理,获得小波包重构信号.

3 实验与分析

利用膜片钳在无离子通道开放时采样10 000个数据点,采样频率为1 k Hz,该时间序列为背景噪声,由于低通滤波和混叠效应,背景噪声近似白色,其均值为0.006 6 pA,方差σ2ω为0.59,并且服从Gauss分布,记为φ(ωt)=N(0,0.59).对这个采样时间序列乘以适当的系数(这里为1.302),使其标准差等于1,记此序列为{ωt},代表膜片钳技术记录细胞膜上单个离子通道电流信号时的背景噪声.

产生一个采样点为10 000的M arkov序列{st},序列长度T=10 000,有两个电流幅值水平0 p A和2 pA,状态Q=(0 pA,2 pA),转移概率为a11=a22=0.95,a12=a21=0.05,此Markov序列为模拟的离子电流信号,如图2所示(图中仅显示前1 000个点).此时,信噪比SNR=2.0,定义为通道最大开放电流幅值的绝对值与噪声标准差之比.将噪声{ωt}叠加到信号{st}上得到膜片钳采样时间序列{yt},模拟M arkov信号淹没于背景噪声中,如图3所示.

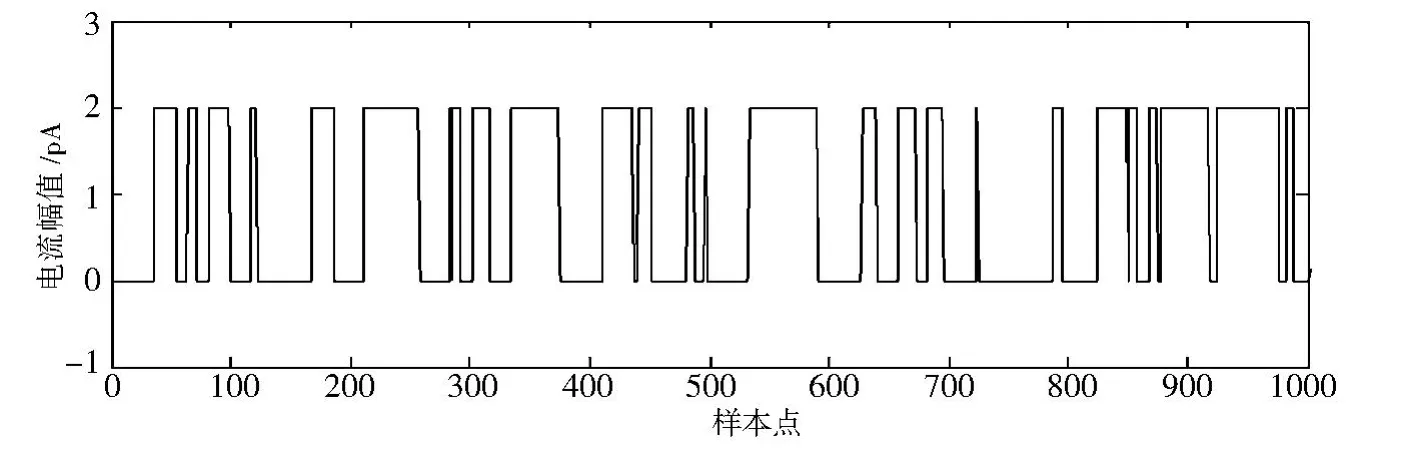
图2 模拟的两状态离子电流信号Fig.2 A simulative ionic current signal{st}

图3 模拟的膜片钳测量时间序列Fig.3 A simulative sequence for patch-clamp recordings{yt}

对{yt}采用四层 Harr小波包分解,图4所示为第四层各频段分解系数,文中仅显示出了前8个.根据尺度能量定义,对分解得到的各频段系数求能量,并由式(5)获得尺度能量分布如图5所示.

图4 小波包分解第四层信号Fig.4 Fourth layer signals based on the wavelet package decomposing

图5 尺度能量分布图Fig.5 Scale-power distribution

由尺度能量分布图可知,第1、2和4频段上所占能量较大,即对应于小波包分解得到的[4,0]、[4,1]和[4,3]系数,认为这些系数包含了大量的离子通道电流信号成分,对该频段对应的系数依照公式(3)进行小波包重构,重构信号Y=F40+F41+F43,对重构信号Y再经过阈值平滑处理,获得离子电流恢复信号,如图6所示.与图3理想的两状态马尔可夫离子电流信号相比,误差率ER=7.85%,ER定义为离子电流幅值被恢复错误的采样点数与采样序列长度T的比值.由此可知,在信噪比SNR=2时,采用小波包算法,离子电流恢复误差完全可以满足膜片钳系统数据分析的要求(ER＜10%).本实验中还采用小波变换的方法,对模拟的同一离子单通道膜片钳测量时间序列进行了12层小波分解及重构,在相同信噪比SNR=2时,得到的电流恢复误差率ER=23.05%.

图6 小波包恢复的离子电流信号Fig.6 Restored current signal using wavelet package

以上仿真实验结果可知,小波包分解方法重构细胞膜离子单通道电流信号不仅运算简单,算法收敛速度快,与小波算法相比,在低信噪比情况下大大提高了信号的恢复精度,具有强的抗噪能力,可以较好地描述实际对象特性,符合膜片钳实验系统的精度要求.

4 结论

本文利用小波包变换有效地解决了膜片钳系统中强噪声背景下细胞膜离子单通道电流信号的恢复.该方法与小波变换方法比较,对信号的分解更加精细,克服了小波变换随着尺度的增加频率分辨率降低的缺陷,提高了电流恢复精度和抗噪能力.同时,与 HMM方法相比,该方法对离子通道状态数目这一先验信息不需要事先确知,且运算简单,算法收敛速度快,为细胞膜离子通道信号分析提供了一种有效方法.

[1] Feng Qin.Restoration of Single-Channel Currents Using the Segmental K-Means Method Based on Hidden Markov Modeling[J].Biophysical Journal,2004,86(3):1488-1489.

[2] 乔晓艳,李刚,林凌.一种基于混合模型的离子单通道信号重构算法研究[J].电路与系统学报,2007,12(1):33-38.

[3] Niranjan P.Bidargaddi,Madihu Chetty,Joarder Kamruzzaman.Hidden Markov Models Incorporating Fuzzy Measures and Integrals for Protein Sequence Identification and Alignment[J].Proteomics&Bioinformatics,2008,6(2):98-103.

[4] 陈振宇,郭兴蓬,董泽华,等.细胞膜离子单通道的频域分析方法[J].生物医学工程学杂志,2004,21(5):754-158.

[5] 虞湘宾,董涛.一种离散小波变换的快速分解和重构算法[J].东南大学学报,2002,32(4):564-568.

[6] 赵林海,王永和.一种基于正交小波包技术的机车信号记录器数据快速压缩方法[J].铁道学报,2009,31(6):102-103.

[7] 罗静,钟佑明.小波包时频分析方法研究与应用[J].重庆邮电大学学报,2009,21(3):379-387.

[8] 乔晓艳,李刚,林凌.基于随机松弛的离散 HMM参数估计和信号恢复[J].中国生物医学工程学报,2007,26(4):517-518.

Ionic Current Reconstruction for Cell Membrane Based on the Wavelet Package Decomposing

QIAO Xiao-gang1,WU Jin-zhi2,QIAO Xiao-yan2
(1.Department of Computer Science,Shanxi Institute for Youth Administrators,Taiyuan030001,China;2.School of Physics and Electronics Engineering,Shanxi University,Taiyuan030006,China)

Anew approach based on wavelet package algorithm is introduced to reconstruct ionic current.The scale-power distribution of the signal is obtained by the multi-resolution analysis to ionic current using the wavelet package decomposing,and the signals are reconstructed by wavelet package reconstructing algorithm.After smooth filtering,the ideal ionic current is res to red from Markov sequences contaminated by noise.The experimental results show s that this method can precisely reconstruct the ionic current under the lower signal-to-noise ratio,and has fast parameter convergence and strong anti-noise ability.

ionic single channel current;wavelet package decomposition;scale-power distribution;signal reconstruction

TN911.72;Q68

A

0253-2395(2011)01-0071-05＊

2010-07-10;

2010-09-25

量子光学与光量子器件国家重点实验室开放课题(KF201009);山西省高校科技开发项目(批准号:20081001)

乔晓刚(1975-),男,硕士,讲师,主要从事计算机应用方向研究.通信作者:乔晓艳(1969-),女,博士,副教授,目前主要从事信号与信息处理、计算机应用等方向研究.E-mail:xyqiao@sxu.edu.cn