＊ 函数性数据分析中的主成分分析

孟银凤,梁吉业,原曦曦

(1.山西大学数学科学学院,山西太原 030006;2.山西大学计算机与信息技术学院,山西太原 030006)

＊函数性数据分析中的主成分分析

孟银凤1,梁吉业2,原曦曦1

(1.山西大学数学科学学院,山西太原 030006;2.山西大学计算机与信息技术学院,山西太原 030006)

通过对比多元统计分析方法与函数性数据分析方法,分析函数性主成分分析的原理、方法,并在此基础上通过实例来说明函数性数据分析的应用,其中的数据分析结果使用MA TLAB软件编程所得.

多元统计分析;函数性数据分析;主成分分析;MA TLAB软件

在现实生活中,人们需要处理越来越多的具有函数特征的数据,例如证券交易所的多只股票的收盘价、成交价;多个地区气象站测量的多年的日降雨量数据和气温数据等.另外,传统的数据分析(时间序列数据、面板数据分析)依赖很多的假设条件,有较强的结构约束.

函数性数据分析(FDA)是从函数角度对数据进行分析[1],把函数性数据看作一个整体,表示为光滑曲线或连续函数ui(t),i=1,…,N,其中,N表示观测对象(曲线)的个数,t可以表示时间,也可以表示时间以外的其他变量.对于所有的观测对象ui(t),i=1,…,N,不要求它们的观测点t和观测次数Ti,i=1,…,N相同.例如测量10个女孩(0-18岁)的身高,并不要求他们的观测点和观测次数相同.

与传统数据分析相比,FDA具有许多优越性,特别是通过对导数曲线或微分曲线的分析能够挖掘出数据更多的重要信息.关于函数性数据分析人们已经做了一些工作.其中,Ram say[2-3]主要探讨了针对函数性数据的各种预处理的方法和统计分析方法.Robert[4]、Berra[5]和李淳芃等[6]针对某一类特定的函数性数据进行了主成分分析.曲爱丽等[7]利用函数性共同主成分分析方法检验了两组函数性样本的分布情况.

本文主要从主成分分析的角度去研究函数性数据,介绍函数性数据分析中的原理、求解主成分的方法并将其应用于我国1978-2006年财政主要支出情况的分析中,借助Matlab软件编程得到其运行结果.为进一步对函数性数据进行分析寻找突破口和创新点.

1 函数性数据主成分分析原理

在多元统计分析中,记录的是同一时期或时点上对每一观测对象多个变量的数据信息.为了达到简化数据的目的,通常是把大量的原始变量综合为少数几个综合变量.

函数性数据记录了每个观测对象的同一个变量某个区间上很多个时刻的数据信息.如果将时间看作多元数据对应的变量(变化因素),则发现函数性数据分析面临更大的“维数灾难”.基于这种特点,可以将多元主成分分析的技术引入到函数性数据分析中,称为函数性主成分分析.

1.1 多元主成分分析

N个观测对象的p个观测变量xi1,xi2,…,xip,得观测阵 XN×p,假设该观测阵经过标准化处理.将p个变量综合成一个综合变量的最简单的方法是用它们的线性组合[8].即

其中β=(β1,β2,…,βp)′,xi=(xi1,xi2,…,xip)′,fi表示第i个观测对象的主成分得分.加权系数β不同则得到不同的综合变量,因此p个变量的综合变量可以有多个.综合变量的方差能够综合反映观测变量变动程度的尺度,因而主成分可根据方差来定义.

解特征方程Vβ=λβ,即求V的特征值和单位特征向量,最大特征值对应的单位特征向量为第一主成分的加权系数.第k主成分可类似求得.

第i个样品在第k个主成分上的得分fik=β′k xi.

1.2 函数性主成分分析

设xi(s)(s∈T),i=1,2,…,N为区间T上的平方可积函数,s对应多元主成分分析中的j,s是连续的而j是离散的.将区间T上的x(s)综合为一个综合变量

解特征方程∫v(s,t)β(t)dt=λβ(s).记Vβ(s)=∫v(s,t)β(t)dt,则Vβ(s)=λβ(s).求解特征函数和特征值的方法有:通过对连续的函数进行离散化或对函数进行基函数展开来求解,也可以采用一般的数值积分法,详见文献[2].

可以发现函数性主成分的特征方程和多元主成分的特征方程相似,不同的是这里的β为函数,而非向量.多元分析中观测变量的个数p决定了特征值及特征向量的个数为p,但函数性主成分分析中维数是无限的,观测对象的个数决定了协方差算子的秩为N-1,因此特征方程的非零特征值最多有N-1个.

2 函数性数据主成分分析的应用研究

例1:国家财政的重要职能是通过公共财政政策,调节社会收入分配,促进社会和谐,为经济发展创造良好的社会和政治环境.财政支出的主要方面有:基本建设支出(F1);增拨企业流动资金(F2);挖潜改造资金和科技三项费用(F3);地质勘探费(F4);工、交、流通部门事业费(F5);支农支出(F6);文教、科学、卫生支出(F7);社会保障支出(F8);国防支出(F9);行政管理费(F10);政策性补贴支出(F11).财政支出结构的变化是对经济、社会不断发展变化的一个反映,利用主成分分析对表1中我国1978-2006年财政主要支出情况进行分析.

在MA TLAB程序中,采用三次样条插值法得到11项财政支出的函数图像如图1,为计算简便,记自变量(年份序号)为1-29.

另外,采用三次样条插值法得到每年的平均财政支出以及标准差函数图像,如图2和图3所示(P24).从均值曲线可以明显看出各项财政支出的平均变化趋势是逐年增加的,且增长速度加快.由标准差曲线可以看出,各项支出额之间的差异随时间的变化也增加.在本文中,采用一般的数值积分法求解Vξ=λξ的特征值共有29个,特征值总和18 160 443.179,前五个特征值及其贡献率和累计贡献率见表2(P24).

图1 11项财政支出函数图像Fig.1 11 fiscal expenditure function

表1 基本建设支出等指标的年度统计(单位:亿元)Table 1 Annual statistics of the basic construction etc(unit:100 million yuan)

图2 平均财政支出函数Fig.2 Average fiscal expenditure function

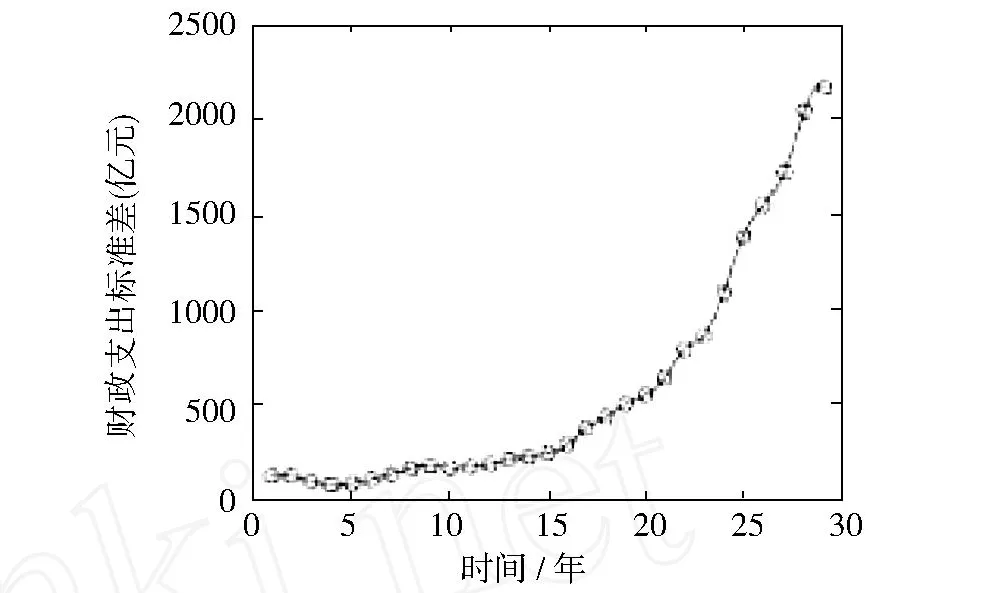
图3 财政支出标准差函数Fig.3 Standard deviation function of fiscal expenditure

表2 特征值和贡献率Table 2 Eigenvalues and contribution efficiency

前两个主成分系数见表3.

表3 前两个主成分系数Table 3 The prior two principal component coefficients

拟合为函数记为主成分的系数函数,见图4和图5.

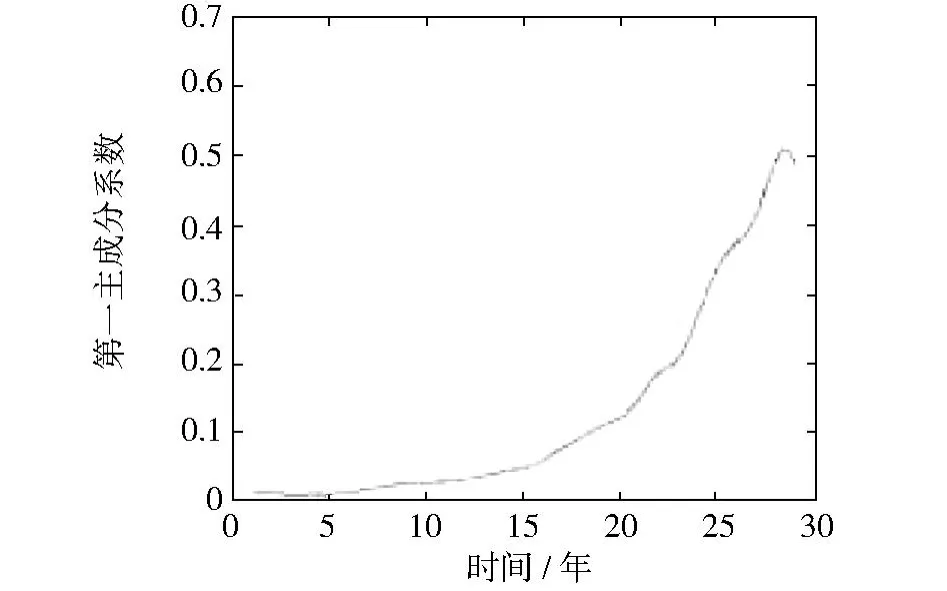
图4 第一主成分系数函数Fig.4 1st principal component coefficient function

图5 第二主成分系数函数Fig.5 2nd principal component coefficient function

分别将前两个主成分的系数函数β1(t)和β2(t)代入(5)式,得到11项指标在第一主成分和第二主成分上的具体得分见表4(P25).

表4 各指标在第一主成分和第二主成分上的具体得分Table 4 The specific scores of each index on the first and the second principal component

从表4中可以看到,第一主成分对基本建设支出(F1)、工、交、流通部门事业费(F5)、支农支出(F6)、文教、科学、卫生支出(F7)、国防支出(F9)、行政管理费(F10)有较大的影响,其余的增拨企业流动资金(F2)、挖潜改造资金和科技三项费用(F3)、地质勘探费(F4)、工、交、社会保障支出(F8)、政策性补贴支出(F11)受到第一主成分和第二主成分的共同影响.

由上可知,函数性主成分分析可以对无限维度的数据进行降维处理,这样大大简化了运算.事实上,我们还可以利用主成分对样本分类等.

[1] Ram say JO.When the Data are Functions[J].Psychometrika,1982,47(4):379-396.

[2] Ram say JO,Silverman B W.Functional Data Analysis[M].北京:科学出版社,2006:161-166.

[3] Ram say JO,Li Xiao-chun.Curve Registration[J].Journal of the Royal Statistical Society:Series B,1998,60(2):351-363.

[4] Roberto V G.Functional Principal Component Analysis of FM RIData[J].Human B rain Mapping,2005,24(2):109-129.

[5] Barra V.Analysis of Gene Expression Data Using Functional Principal Components[J].Computer Methods and Programs in Biomedicine,2002,75(1):1-9.

[6] 李淳芃,王兆其,夏时洪.人体运动的函数数据分析与合成[J].软件学报,2009,20(6):1664-1672.

[7] 曲爱丽,朱建平.函数型数据的共同主成分分析探究及展望[J].统计与信息论坛,2009,24(2):19-23.

[8] 高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005.

Principal Component Analysis in Functional Data Analysis

M ENG Yin-feng1,L IANG Ji-ye2,YUAN Xi-xi1
(1.School of Mathematical Science,Shanxi University,Taiyuan030006,China;2.School of Computer and Information Technology,Shanxi University,Taiyuan030006,China)

The principle and method of principal component analysis about the functional data are given by comparing multivariate statistical analysis methods with functional data analysis methods.Moreover,it gives some examples to illustrate their application and analyzes the data by using MATLAB software.

multivariate statistical analysis;functional data analysis;principal component analysis;MA TLAB software

O212.4

A

0253-2395(2011)01-0021-05＊

2010-06-28;

2010-09-08

国家自然科学基金(71031006)

孟银凤(1979-),女,山西大同人,讲师,硕士,从事概率统计研究.E-mail:mengyf@sxu.edu.cn