可微C0－半群的谱

赵华新

（延安大学 数学与计算机科学学院，陕西 延安 716000）

可微C0－半群的谱

赵华新

（延安大学 数学与计算机科学学院，陕西 延安 716000）

利用可微C0－半群的若干性质给出了可微C0－半群｛T（t）：t≥0｝的生成元A的谱与AT（t）的谱之间的关系.

C0－半群；可微；谱；点谱；剩余谱

在经典的算子半群理论中，谱映射定理是其非常重要的组成部分.文献［1］讨论了C0－半群的谱与其生成元的谱之间的关系，特别阐述了C0－半群的点谱、连续谱、剩余谱与其生成元的点谱、连续谱、剩余谱之间的关系，得到了非常完美的结果.本研究在此基础上，讨论了可微C0－半群谱与其生成元的谱之间的关系，对它们的点谱、剩余谱之间的关系做了初步探讨.

本研究假设X为Banach空间，ρ（A），σ（A），σp（A），σr（A）分别表示算子A的预解集、谱集、点谱集、剩余谱集，R（A）表示A的值域.

定义［1］｛T（t）：t≥0｝为Banach空间X上的C0－半群，若对任意x∈X，t→T（t）x作为t的函数，当t＞t0时关于t可微，则称C0－半群｛T（t）：t≥0｝当t＞t0是可微的；若C0－半群｛T（t）：t≥0｝当t＞0时是可微的，则称C0－半群｛T（t）：t≥0｝是可微的.

引理1［1］设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，则有σ（T（t））⊃etσ（A）.

引理2［2］设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0时是可微的，则对任意λ∈σ（A），当t＞t0时，有λeλt∈σ（AT（t）），即σ（AT（t））⊃λetσ（A）.

引理3［1］设C0－半群｛T（t）：t≥0｝当t＞t0时是可微的，其无穷小生成元为A，则对于t＞nt0，T（t）：X→D（A），T（n）（t）＝AnT（t），n＝1，2，…为有界线性算子.

注意到（eλt）′＝λeλt，比较引理1，引理2，考虑到引理3所给出的可微C0－半群的性质，猜想：对于可微C0－半群，当λ∈σ（A）时，（eλt）″＝λ2eλt是否属于T″（t）＝A2T（t）的谱集，即是否成立

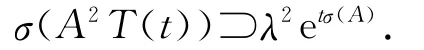
对此，本研究有如下定理.

定理1 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0是可微的，则对任意λ∈σ（A），当t＞2t0时，有λ2eλt∈σ（A2T（t）），即

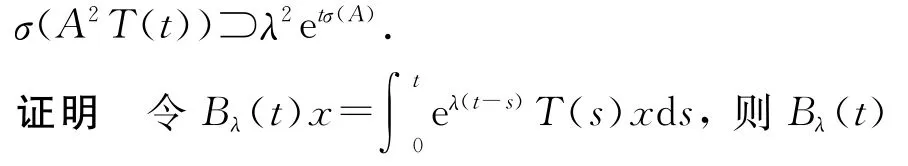
关于t是可微的，且有（Bλ（t）x）′＝T（t）x＋λBλ（t）x，由此可见，Bλ（t）为X上的有界线性算子.

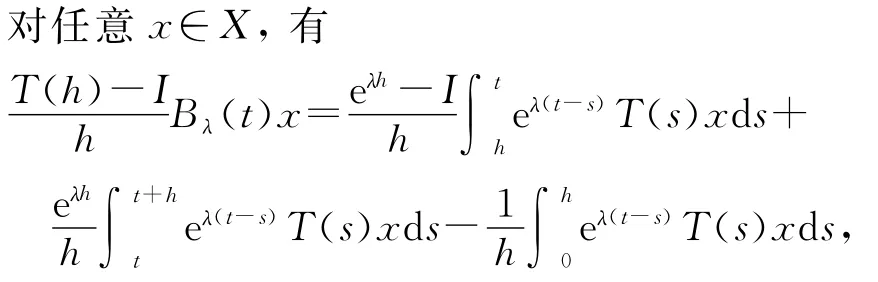
令h→0＋，则上式右端趋于λBλ（t）x＋T（t）xeλtx，由无穷小生成元的定义知x∈D（A），且

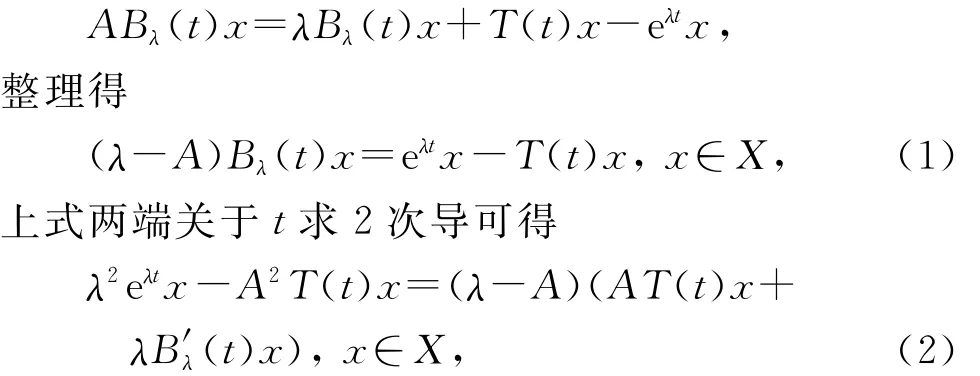
令C（t）x＝λ2eλtx－A2T（t）x，则C（t）为有界线性算子.设λ∈σ（A），若λ2eλt∈ρ（A2T（t）），则C（t）可逆，且由式（2）可知有

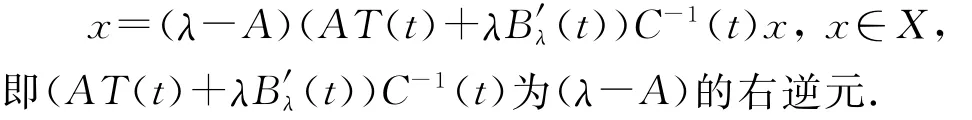
同时，由于C（t）与T（s）可交换，从而C（t）与Bλ（t）可交换，进而可以验证C（t）与 （AT（t）＋λB′λ（t））可交换.

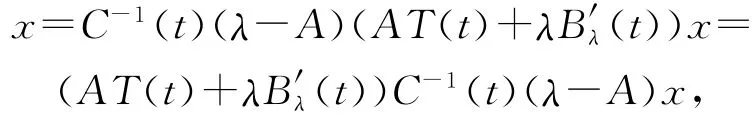
这表明（AT（t）＋λB′λ（t））C－1（t）是（λ－A）的左逆元.所以有λ∈ρ（A），矛盾.从而当λ∈σ（A）时，必有λ2eλt∈σ（A2T（t）），即σ（A2T（t））⊃λ2etσ（A）.

推论1 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0时是可微的，则对任意λ∈σ（A），当t＞nt0时，有λneλt∈σ（AnT（t）），n＝1，2，…，即

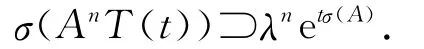
推论1的证明与定理1的证明类似.

下面讨论对于可微C0－半群｛T（t）：t≥0｝，AT（t）的点谱、剩余谱与其生成元A的点谱、剩余谱之间的关系，得到如下结论.

定理2 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0是可微的，则对任意λ∈σ（A），当t＞t0时，有λeλt∈σp（AT（t）），即

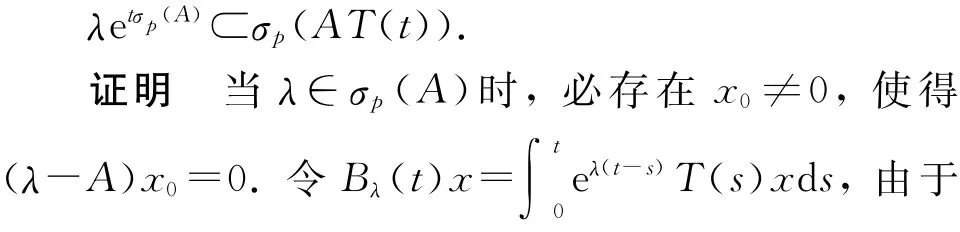
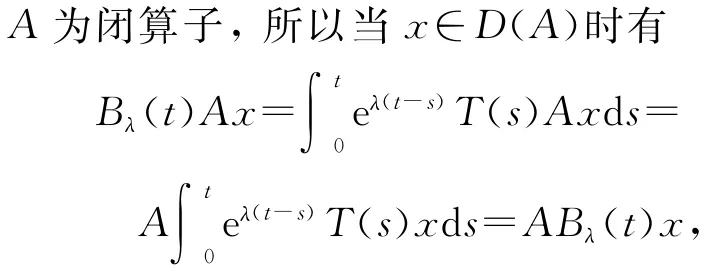
再利用式（1）可得

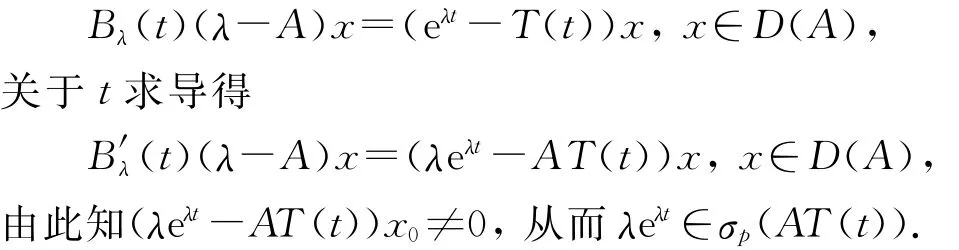
推论2 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0是可微的，则对任意λ∈σ（A），当t＞nt0时，有

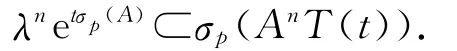
推论2的证明与定理2的证明类似.

定理3 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0时是可微的，则对于λeλt∈σp（AT（t）），当t＞t0时，存在自然数k，使得

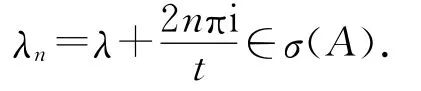
证明 设λeλt∈σp（AT（t）），则存在x0≠0，使得（λeλt－AT（t））x0≠0.f（s）＝λe－λsAT（s）x0作为s的函数不恒为零，将f（s）以t为周期进行奇式或偶式延拓，其Fourier系数必有一个不为零.从而存在自然数k，使得

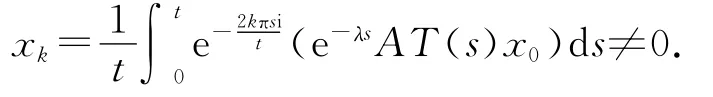
令‖T（t）‖≤Meωt，则当Reμ＞ω时，利用A的闭性可得

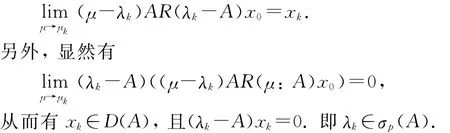
定理4 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0是可微的，则对任意λ∈σr（A），当t＞2t0时，有λeλt∈σr（AT（t）），即有

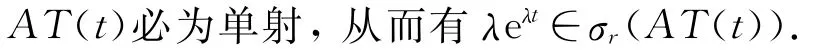
推论3 设｛T（t）：t≥0｝为一C0－半群，其无穷小生成元为A，如果｛T（t）：t≥0｝当t＞t0时是可微的，则对任意λ∈σr（A），当t＞nt0时，有λneλt∈σr（AnT（t）），即有

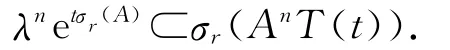
推论3的证明类似于定理4的证明.

利用本研究方法有可能对n次积分C半群的谱映射定理［3］以及α次积分C半群的谱映射定理［4］做进一步研究.

［1］ Pazy J H.Semigroups of Linear Operators and Applications to Partial Differential Equations［M］.New York：Spring－Verlag，1983.

［2］ 周鸿兴，王连文.线性算子半群理论及应用［M］.济南：山东科学技术出版社，1994.

［3］ 秦喜梅.n次积分C半群的谱映射定理［J］.安徽师范大学学报：自然科学版，2008，31（1）：16－19.

［4］ 杨雯雯，赵华新.α次积分C半群的谱映射定理［J］.西南民族大学学报：自然科学版，2009，35（3）：462－467.

Spectrum of differentiableC0－semigroups

ZHAOHuaxin
（College of Mathematics and Computer Science，Yan’an University，Yan’an 716000，Shaanxi Province，China）

By using the properties of differentiableC0－semigroups，the relationships between the spectrum of infinitesimal generatorsAofC0－semigroups｛T（t）：t≥0｝and the spectrum ofAT（t）are discussed.

C0－semigroups；differentiable；spectrum；point spectrum；residual spectrum

O177.31

A

1671－1114（2011）01－0029－02

2010－04－06

陕西省教育厅专项科研计划项目（08JK497）

赵华新（1964—），男，教授，硕士，主要从事应用泛函分析方面的研究.

（责任编校 马新光）