工作状态下加筋土挡墙土压力分布规律研究

周亦涛,梁小勇,王蓉蓉,薛晓辉,王道远

(1.河北工程技术高等专科学校水利工程系,河北沧州 061001;2.河北科技大学建筑工程学院,河北石家庄 050018;3.陕西铁路工程职业技术学院建筑工程系,陕西渭南 714000;4.河北交通职业技术学院土木工程系,河北石家庄 050091)

工作状态下加筋土挡墙土压力分布规律研究

周亦涛1,梁小勇2,王蓉蓉1,薛晓辉3,王道远4

(1.河北工程技术高等专科学校水利工程系,河北沧州 061001;2.河北科技大学建筑工程学院,河北石家庄 050018;3.陕西铁路工程职业技术学院建筑工程系,陕西渭南 714000;4.河北交通职业技术学院土木工程系,河北石家庄 050091)

加筋土挡墙墙背侧向土压力的计算方法都不能很好地解释工作状态下的分布情况,现场测试表明土压力沿墙高呈上下小、中间大的形式分布。微元体法得出的重力式挡墙墙背主动土压力与静止土压力分布形式与加筋土挡墙现场测试结果比较接近,然而2种土压力进行组合后,分布形式吻合得非常好,但大小相差比较大。综合考虑了拉筋垂直层间距与填料的影响,提出了加筋土挡墙墙背土压力计算模型,并对模型中的拉筋层竖向间距对加筋土挡墙墙背土压力的影响系数进行了初步探讨,然后与现场测试结果进行了对比分析,证实了该模型的合理性。

侧向土压力;加筋土挡墙;土压力系数;竖向间距

加筋土挡墙设计的关键是拉筋拉力的计算,而拉筋拉力是用来抵消墙背土压力的[1]。因此,加筋土挡墙设计的关键实质上是怎样确定墙背土压力。墙背土压力的计算,目前有库仑合力法、库仑力矩法、正应力均匀分布法、正应力梯形分布法、正应力梅氏分布法、Osman能量法、经验法和公路变系数法[2]等,都是对朗肯土压力理论进行修正,且填土表面有荷载下土中应力的影响都是按一定的角度扩散的[3]。其中公路变系数法较其他方法能合理解释一些实际土压力分布情况,因而在加筋土挡墙设计中得以广泛应用。但这些计算理论都是基于极限平衡理论的,而挡墙在工作状态下并没有达到极限状态,因而加筋土挡墙墙背土压力分布非上述理论能解释。

许多研究人员用微元体法对处在主动极限状态下的滑楔体进行了研究,得出了墙背土压力沿墙高呈上下小、中间大的曲线分布公式[4～9]。目前,加筋土挡墙现场测试研究结果表明墙背土压力沿墙高呈上下小、中间大的分布形式[10,11],因而笔者将利用他们的研究成果,并对筋材竖向间距加以考虑,来对加筋土挡墙墙背侧向土压力分布进行探讨。

1 重力式挡墙墙背土压力

假设挡墙高 h(m),填土表面水平且有均布荷载q(kN/m),无黏性填土容重为γ(kN/m3)。墙后填土沿破裂角为θ的破裂面沿下有滑动趋势,其微元体受力如图1所示[4]。

距离填土表面z处的挡墙墙背土压力按王元占等推导的公式[4]计算:

图1 填土微元体受力简图Fig.1 Forces acting on differential element of backfill

2 加筋土挡墙墙背土压力计算

2.1 工作状态下的墙背侧向土压力计算

工作状态下,挡墙墙背土压力一般处在主动土压力与静止土压力之间,且沿墙高呈上下两端小、中间大的曲线分布[4～9],挡墙总会出现一定的位移(可能是平移、绕墙趾转动)[7,12],墙趾处位移微小。笔者认为墙趾处不发生位移,墙顶处为主动土压力,墙趾处为静止土压力,则可按式(4)来计算墙背土压力(简称组合法土压力)。

式中:σL为距离填土表面 z处的重力式挡墙墙背侧向土压力;σa按式(2)计算;σ0按式(3)计算。

式(4)适合于计算重力式挡墙背向填土的位移情况;也适合于加筋土挡墙,因为加筋土挡墙一般来说不会发生挤压填土的情况。

2.2 加筋土挡墙墙背土压力计算模型

式(4)计算得出的加筋土挡墙墙背侧向背土压力偏大,这是因为该计算式没有考虑筋材的作用。笔者在考虑拉筋竖向层间距影响的情况下,建立了如式(5)所示的模型来计算加筋土挡墙墙背土压力(简称加筋组合法土压力)。

式中:σ为距离填土表面z处的加筋土挡墙背侧向土压力;f(s)为加筋土挡墙土压力拉筋竖向间距影响系数,f(s)=1-e-λs,λ为由填土与筋材物理特性所决定的系数,且λ>0;s为拉筋层间距;σL按式(4)计算。

2.3 模型的合理性分析

由于λ>0,则d f(s)/d s>0,所以加筋土挡墙墙背土压力随筋材竖向间距的增加而增加。

当s=0时,f(0)=0,则有σ=0。这说明墙后全是筋材而没有填土的时候,墙背没有压力,这与筋材的自立性相符合。

当s→+∞时,f(+∞)=1,则有σ=σL。即加筋土挡墙墙背土压力随筋材竖向间距的增加而增加,且有界。说明没有拉筋的时候墙背土压力就是重力式挡墙墙背土压力。

由于筋材竖向间距s的取值为(0,+∞),则加筋土挡墙墙背土压力σ的相应取值为(0,σL)。以上的讨论,说明了式(5)计算加筋土挡墙墙背土压力的合理性。

2.4 模型中参数λ的确定

模型中的参数λ与回填土的物理特性及筋材的物理特性有关。填土压缩模量与内摩擦角越大,筋土间相互作用越大,墙背土压力也越大;筋材的弹性模量越大,墙背土压力越小。则拟将按式(6)确定参数λ。

式中:Ef为筋材的弹性模量(M Pa);Es为回填土的压缩模量(M Pa);vs为回填土的泊松比。

没有材料的物理参数时,对土工格栅拉筋加筋土挡墙可以取λ=2.5。当s=1时,f(1)=1-e-2.5×1=0.92≈1,这说明拉筋层间距不宜大于1 m。

2.5 模型的试验验证

例1 赣(州)龙(岩)铁路线上某段加筋土挡墙,墙高 h=12.2 m,填土表面荷载 q=0,墙体上部4.7～12.2 m,填土容重γ=17 kN/m3,内摩擦角φ=22°,弹性模量 Es=25 M Pa,泊松比 vs=0.3,拉筋采用A型,其弹性模量 Ef=2 515 M Pa;墙体下部0～4.7 m填土容重γ=19.2 kN/m3,内摩擦角φ=35°,弹性模量Es=55 M Pa,泊松比 vs=0.3,拉筋采用B型,其弹性模量 Ef=2 017 M Pa。整个挡墙的拉筋竖向间距s=0.5 m,这里取填土与墙背之间的摩擦角δ=φ/2[13]。

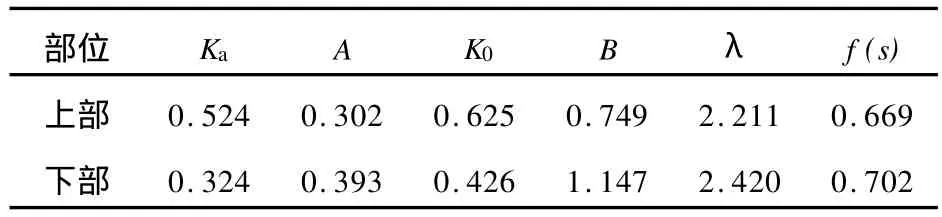
表1 土压力参数计算结果Tab.1 Parameters calculation of lateral soil p ressure

参数计算结果见表1,加筋土挡墙竣工后墙背侧向土压力实测值与理论值的比较见图2。从图2可以看出,实测值与理论值相当接近,差值都在5 kPa左右,实测与理论最大值基本上在同一高度,且中下部土压力较大处误差相差10%左右,说明加筋土挡墙墙背土压力实测值与理论值非常吻合。因此,加筋组合法土压力能有效反映工作状态下的墙背土压力分布。

例2 梅(州)坎(市)铁路某路堤双级加筋土挡墙上级墙,墙高 h=6.4 m,填土容重γ=19 kN/m3,内摩擦角φ=35°,拉筋竖向间距 s=0.3 m[14,15]。其他参数缺失 ,取 q=20 kPa,δ=φ/2,λ=2.5,则f(s)=0.528。理论计算与实测值的比较见图3,实测最大值与理论值相当接近,其误差在10%以内。从图3可以看出,本模型计算出的土压力对台阶式加筋土挡墙上级墙也是比较有效的。

图2 加筋土挡墙侧向土压力分布图Fig.2 Distribution of lateral soil p ressure of reinforced earth retaining wall

从以上2个例子可以看出,笔者的模型计算值都大于实测值,因此本模型是偏于安全的,可以用于指导施工与设计。

3 结 论

通过以上的研究分析,得出如下结论。

1)笔者提出的加筋土挡墙墙背侧向土压力计算模型较好地反映了土压力随墙高呈中间大、上下小的分布规律,即土压力先随加筋填土深度的增加而增加,达到最大值后便开始减小。对单级加筋土挡墙,本模型与实测值吻合得尤其好,不但分布形式一致,而且几乎在同一位置出现最大值。

2)本模型计算值与实测值相当接近,在中部出现最大值处误差在10%左右。且笔者提出的加筋组合法土压力值都比实测值大,是偏于安全的,可以用于指导施工设计。

3)拉筋竖向间距影响系数随竖向间距的增加而增加,墙背土压力也随着增加,但竖向间距大于1 m后影响系数增加很微小,土压力也基本上没有什么变化。因而拉筋竖向间距不宜大于1 m。

4)笔者的研究只是一种尝试,需要大量的试验来进一步研究。

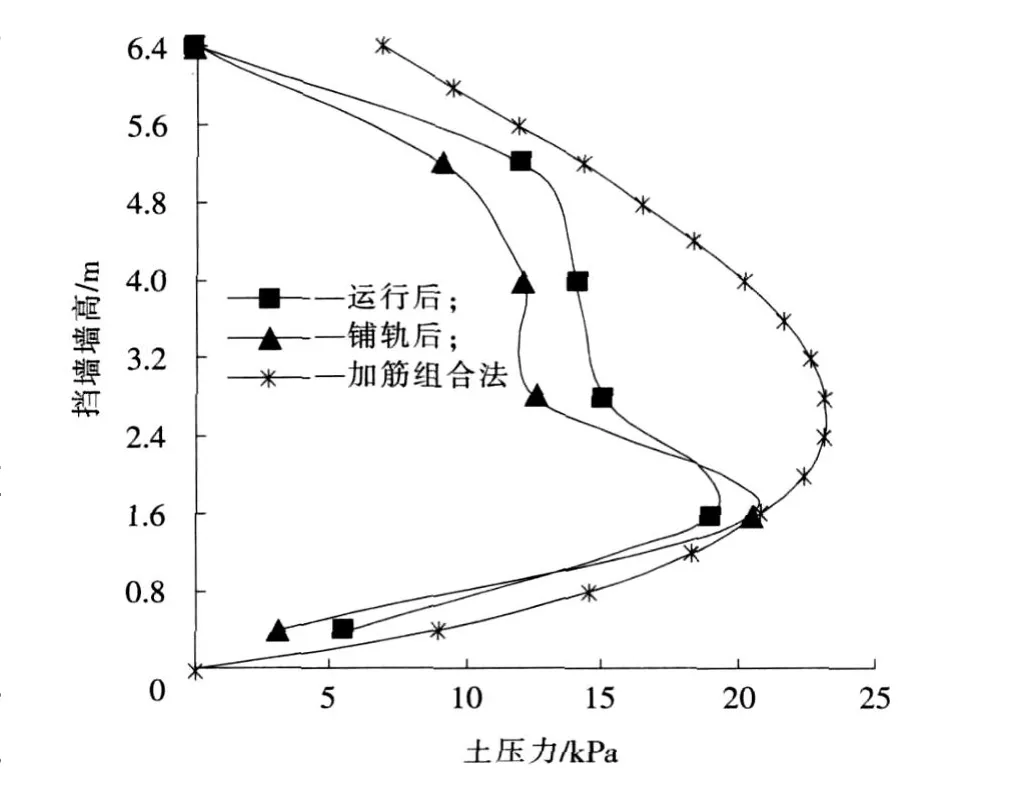
图3 多级台阶式加筋土挡墙侧向土压力分布图Fig.3 Distribution of lateral soil p ressure of multi-steps reinforced earth retaining wall

[1] 凌天清,曾德荣.公路支挡结构[M].北京:人民交通出版社,2006.

[2] 张师德,吴邦颖.加筋土结构原理及应用[M].北京:中国铁道出版社,1986.

[3] 杨广庆.路基工程[M].北京:中国铁道出版社,2003.

[4] 王元占,李新国,陈楠楠.挡土墙主动土压力分布与侧压力系数[J].岩土力学(Rock and Soil M echanics),2005,26(7):1 019-1 022.

[5] 刘忠玉,马德遂,何盛东.层状填土的主动土压力计算[J].郑州大学学报(工学版)(Journal of Zhengzhou University(Engineering Science)),2004,25(3):56-59.

[6] 蒋希雁,宋思忠.层状填土的主动土压力的理论研究与计算分析[J].建筑科学(Building Science),2006,22(6):22-24.

[7] 高 军.复合土钉支护技术在软岩高边坡防护中的应用及其作用机理[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2004,25(2):69-73.

[8] 岳祖润,彭胤宗,张师德.压实粘性土填土挡土墙土压力离心模型试验[J].岩土工程学报(Chinese Journal of Geotechnical Engineering),1992,14(6):90-96.

[9] 陈雪华,律文田,王永和.桥台台背土压力的试验研究[J].岩土力学(Rock and Soil Mechanics),2006,27(8):1 407-1 410.

[10] 唐辉明,林 彤.三峡工程库区巫县加筋土挡墙离心模型试验研究[J].岩石力学与工程学报(Chinese Journal of Rock Mechanics Engineering),2004,23(17):2 893-2 901.

[11] 周世良,何光春,汪承志,等.台阶式加筋土挡墙模型试验研究[J].岩土工程学报(Chinese Journal of Geotechnical Engineering),2007,29(1):152-156.

[12] 梅国雄,宰金珉.考虑变形的朗肯土压力模型[J].岩石力学与工程学报(Chinese Journal of Rock Mechanics Engineering),2001,20(6):851-853.

[13] 杨广庆.土工格栅加筋土挡墙水平变形研究[D].北京:北京交通大学,2005.

[14] 王 祥,徐林荣.双级土工格栅加筋土挡墙的测试分析[J].岩土工程学报(Chinese Jouranl of Geotechnical Engineering),2003,25(2):20-24.

[15] 范春起.风压式高层建筑外墙清洗机的控制系统[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2003,24(4):77-81.

Study on distribution of working lateral soil p ressures fo r reinfo rced earth retaining w all

ZHOU Yi-tao1,L IANG Xiao-yong2,WANG Rong-rong1,XUE Xiao-hui3,WANGDao-yuan4
(1.Department of Hydraulic Engineering,Hebei Engineering and Technical College,Cangzhou Hebei 061001,China;2.College of A rchitecture Engineering,Hebei University of Science and Technology,Shijiazhuang Hebei050018,China;3.Department of Civil Engineering and A rchitecture,Shaanxi Railway Institute,Weinan Shaanxi714000,China;4.Departmentof Civil Engineering,Hebei Jiaotong Vocational and Technical College,Shijiazhuang Hebei 050091,China)

A t p resent,no methods fo r lateral soil p ressure of reinfo rced earth retaining wall can explain the distribution of wo rking p ressure.The site tests show that the lateral soil p ressure is distributed w ith greater value in the middle and less though at the bo ttom and the top.The distribution of the active and static soil p ressure in the gravity retaining wall,w hich is obtained acco rding to differential element method,is quite close to the site tests of the lateral soil p ressure in reinforced earth retaining wall.The linear combination of the active and static soil p ressure is consistent w ith the site test in shape,but not in values.Acco rding to soil p ressure combination,lateral soil p ressuremodel considering vertical spacing of in reinforced earth retaining wall was put forward.This paper discusseed influence coefficient of the vertical spacing of the reinforcement to the lateral soil p ressure in reinfo rced earth retaining wall.Then the model was confirmed by the site tests and the results show the reasonability of the model.

lateral soil p ressure;reinfo rced earth retaining wall;coefficient of earth p ressure;vertical spacing

TU 43

A

1008-1542(2010)01-0067-04

2009-06-15;责任编辑:冯 民

周亦涛(1978-),男,四川宣汉人,讲师,硕士,主要从事土木工程方面的教学与研究。