粮食产量预测的支持向量机模型研究

向昌盛，周子英，武丽娜

（湖南农业大学a.东方科技学院；b.资源环境学院，湖南 长沙 410128）

粮食产量预测的支持向量机模型研究

向昌盛a，周子英b，武丽娜b

（湖南农业大学a.东方科技学院；b.资源环境学院，湖南 长沙 410128）

粮食产量的历史数据有限，是典型的小样本数据，又由于粮食产量受不确定性因素的影响，是一个复杂的非线性系统，以往的粮食产量时间序列预测模型的阶数采用经验方法或线性方法来确定，得到的预测精度不理想。针对这些问题，可将支持向量机引入到时间序列模型定阶的方法中，然后采用留一法交叉验证寻找最优参数，建立一个多输入、单输出的预测模型。通过对中国粮食产量进行仿真实验，并与一次滑动平均、ARIMA、LS_SVM和 RBF神经网络的预测模型作比较来验证模型的有效性，结果表明该模型该有较高的预测精度和较强的泛化能力，证明了该模型对近期粮食产量的预测是可靠的。

粮食；产量预测；支持向量机；时间序列

一、问题的提出

农业是国民经济的基础，粮食生产是农业的关键。预测未来一段时间粮食产量的变化情况，可以为政府科学决策提供依据，也便于为粮农、企业提供决策参考。粮食产量数据是一种高度不稳定、复杂且难以预测的时间序列数据，这些数据往往既隐含大量的动态特征，又受自变量的影响，同时具有高度的非线性[1]。国内外的相关研究中，不少学者构建了许多很有价值的理论假说和预测模型，主要包括时间序列方法、回归分析法和人工神经网络方法等。时间序列方法中最具代表性的差分自回归移动平均(autore-gressive integrating moving average，ARIMA)，ARIMA是基于线性数据的模型，但粮食时间序列数据往往更多地表现为非线性且含有复杂的噪声，这样基于线性模型定阶获得的模型阶数和保留变量的ARIMA模型，往往并非最优，从而导致预测精度不高[2]。采用回归分析法[3]是基于固定模型的，而粮食产量是非线的，而且具有混沌性，所以采用回归分析法无法捕捉到粮食产量数据的非线性特征，预测结果失真。王启平[4]、禹建丽[5]等利用神经网络对粮食产量进行了预测，取得了不错的效果，但是神经网络要求数据样本大，而粮食产量数据属于小样本数据，所以在预测过程中常出现结果过拟合，泛化能力不强等现象。Vapnik等[6]根据统计理论提出了支持向量机(support vector machines，SVM)学习方法，SVM 的最大特点是改变了传统的神经网络基于经验风险最小化原则，较好地解决了小样本、非线性、过拟合、维数灾和局极小等问题，SVM已经逐步应用于各个领域的预测中[7-9]，李晓东[10]等利用最小二乘支持向量机(least squares support vector machines，LS_SVM)对我国粮食产量进行了预测，得到的结果比较好。但LS_SVM 通过构造损失函数将原支持向量机算法的二次优化问题转化为求解线性方程，牺牲了预测精度，失去了SVM稀疏性的优点，不能保证是全局最优解[11,12]。

总之，粮食产量的历史数据有限，是典型的小样本数据，同时由于粮食产量受不确定性因素影响的，是一个复杂的非线性系统，以往的粮食产量时间序列预测模型的阶数采用经验方法或线性方法来确定，得到的预测精度不理想，针对这些问题，笔者将SVM引入到粮食产量的模型定阶和预测中，建立一种基于支持向量机的预测模型，并与一次滑动平均、ARIMA、LS_SVM和RBF神经网络的预测模型作了比较来验证模型的有效性。

二、粮食产量预测的支持向量机模型

1.时间序列模型的定阶

建立时间序列模型最为关键的、最困难的是确定模型的阶数。近年来，许多专家和学者对如何确定时间序列的时滞阶数进行了深入研究[13]，模型的阶数选取方法在实践中有两种：一是靠经验选择，二是先设定模型其他参数方法，然后对滞后阶数按照一定的标准进行优化。第一种方法过分依赖研究者的水平和经验，不能客观选择最佳滞后阶数。而第二种方法则忽略了一个重要问题：滞后阶数与其他参数对模型好坏的影响是相互的，如果先人为设定其他参数选择滞后阶数，而后使用该滞后阶数值优化参数，很有可能只是在该滞后阶数下的参数局部最优，而不是全局最优。同时这两种方法都是针对线性模型的，得到的模型对线性时间序列比较理想，但都忽略了时间序列的非线性关系，这样导致对非线性模型，其预测准确性受到很大的限制。针对此问题，笔者将支持向量机引到非线性时间序列模型定阶中，具体步骤如下：

(1)假定一个原始时间序列 n个样本，首先强制性的拓一阶，用留一法进行交叉验证进行支持向量机测试，得到模型的方根误差(Root Mean Square Error，RMSE)；

(2)继续进行下一轮的拓阶，利用相同的方法进行测试，得到本轮的RMSE，对待比较的相邻两模型 SVM(n)和 SVM(n+1)的 RMSE，如果RMSESVM(n)＞RMSESVM(n+1)(RMSESVM(n)为 SVM(n)的均方误差，RMSESVM(n+1)为 SVM(n+1)的均方误差)，重复第(2)步，否则转到下一步；

(3)拓阶停止，此时取SVM(n)模型的阶数为时间序列模型的滞后阶数。

2.时间序列预测模型的建立

假设观察到的时间序列为 (z1,z2,…,zt)，时间序列的SVM预测数学关系表达式为：

步骤 1：数据预处理。为了提高运算速度和预测精度，对样本进行归一化处理，预测处理变换关系式如下：

式中：x'为归一化后的值，xmax，xmin分别为原数据序列中的最大值和最小值。

步骤2：模型的定阶。根据本文提出的基于SVM的非线性定阶方法确定时间模型的滞后阶数，即SVM时间序列模型的输入向量的个数，这样就可以建立一个多输入、单输出支持向量机预测模型。按照式(3)得到支持向量机输入向量和输出向量。

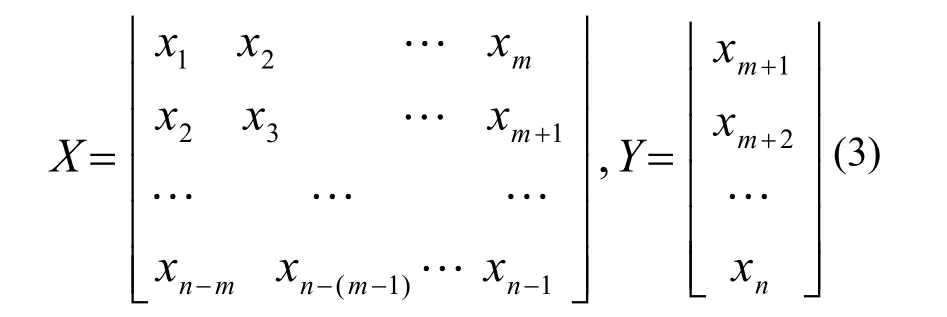
步骤 3：核函数选择。据泛函的有关理论，只要一种核函数 K（x,xi）满足 mercer条件的对称函数均可作为核函数，但是对于特定的问题，如何选择最合适的核，一直是困扰研究者的一个难点，针对此问题，很多研究和实验表明[14]，当缺少过程的先验知识时，选择径向基函数比选择其它核函数效果好。本文核函数采用径向基函数核函数(RBF)。RBF函数定义如下：

式中：其中l为支持向量的个数，xi为作为支持向量的样本因子向量，x为待预报因子向量，ai、和b为建立SVM模型待确定的系数，δ为核参数。

步骤4：模型参数寻优及验证。利用SVM对训练样本集进行学习，通过交叉验证结果找出 SVM模型的最优参数，利用最优参数对验证集进行检验，检验模型的泛化能力。

3.参比模型及评价指标

为了考察SVM模型的优劣，同时采用一次滑动平均、ARIMA模型、LS_SVM和RBF神经网络进行对比实验，所有模型均采用一步预测法。一次滑动平均和ARIMA模型由DPS6.5给出，RBF神经网络和LS_SVM自编程序通过MATLAB7.0调用神经网络工具箱和LS_SVM1.5工具箱；SVM采用LIBSVM2.86版本在 MATLAB7.0平台下实现，LIBSVM 算法是一种将序贯最小优化算法(Sequential Minimal Optimization，SMO)和 Svmlight算法相结合的优化方法，对工作集的选择策略有所改进，各方面性能优于标准SVM。为了评价模型预测性能的优劣，RMSE和MAPE作为模型的评价指标，RMSE和MAPE分别定义如下：

其中，yi为真值，为预测值，n为预测样本数。RMSE仅适用于同一数据集不同模型间的比较，MAPE可用于不同数据集间的比较。但对同一数据集，如A模型与B模型相比虽MAP E较大而RMSE较小，则A模型预测更为稳健，因此，RMSE为主要评价指标。

三、模型的仿真实验

1.数据来源

分析粮食产量的重要性不但体现在对历史数据的拟合上，对未来短期预测也同样重要，准确的预测可以帮助调节粮食需求的市场平衡性，防止出现因为粮食供应不足或过多产生的不良的市场效应。笔者选用的数据为 1978─2007年我国的粮食产量，数据来自于2008年《中国统计年鉴》，如表1所示。将数据分为两部分，1978─2000年的实际产量作为训练样本来拟合和建模，2001─2007年的实际产量作为检验样本来检验模型的泛化能力。

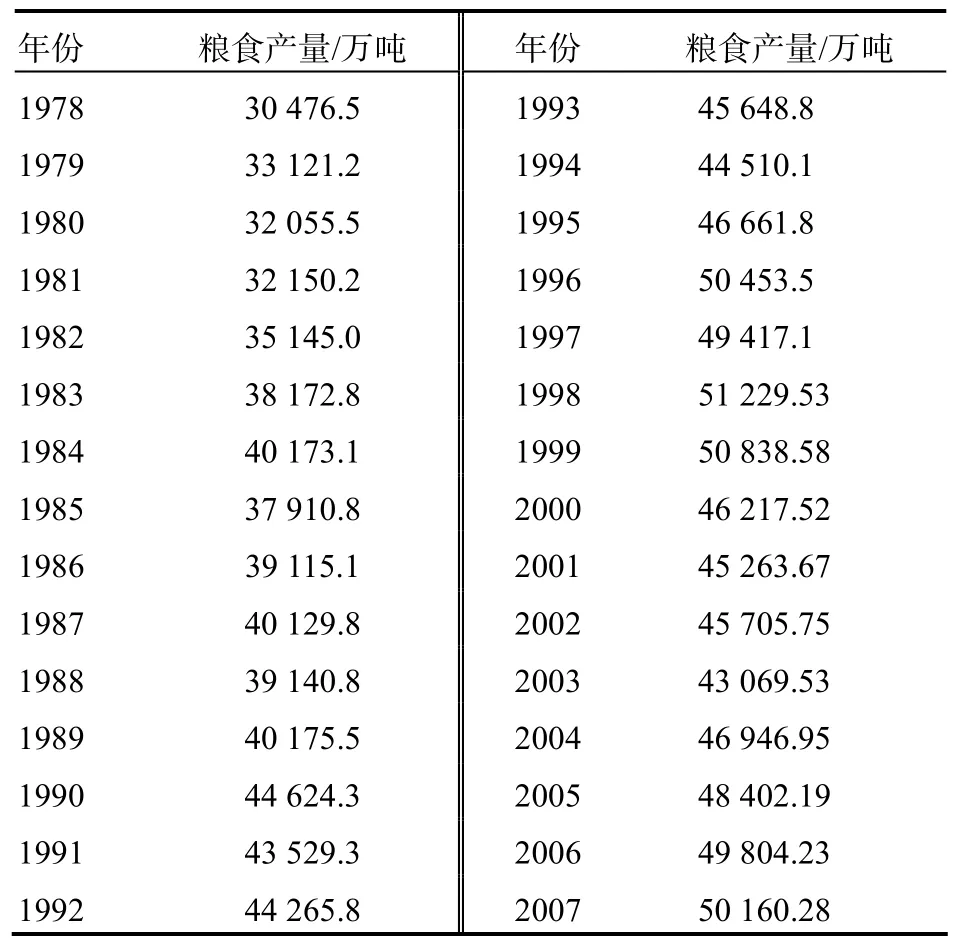
表1 1978─2007年我国粮食产量

2.模型建立与验证

根据模型定阶得到滞后阶数m=3，这就意味着可以将前三年的粮食产量SVM的输入来预测当年的粮食产量。按照式(3)，表格1中的数据可构造样本27组，将前20组作为训练样本，后7组作为检验样本，选用RBF核函数，利用gridregression.py和留一法交叉验证进行模型参数自动寻优，确定最优模型的核函数参数，利用建立的最优模型对1987―2000年的数据进行拟合，然后模型对2001―2007年的粮食产量进行验证，检验模型的泛化能力，结果分别见表2和表3。

3.2008―2010粮食产量预测

用上述训练好的支持向量机模型对我国2008―2010年的粮食产量进行预测，结果如表4。

4.结果分析与讨论

由表2，表3及表5可知，线性模型一次滑动平均和ARIMA预测精度不高，主要是不能捕捉到粮食数据的非线性特征；RBF神经网络精度也不理想，是因为粮食数据属于小样本数据，容易出现局部最优，导致泛化能力差。在所有的模型中，SVM的拟合和泛化预测能力是最好的，这是由于 SVM基于结构风险最小，较好地解决了小样本、非线性、过拟合、维数灾和局极小等问题，泛化推广能力优异。同时说明了基于支持向量机的非线性定阶方法挖掘了时间序列数据之间隐含的非线性关系，使非线性时间序列模型的定阶得到了很好的解决。

利用SVM对2008―2010年我国粮食产量的预测，从表4得知：我国粮食产量在这三年内将稳定在 5.1～5.4亿吨之间，波动不大，基本满足我国人口的增长需要。近年来我国农业生产结构调整力度继续加大，减少了粮食作物的种植面积；西部省份继续落实国家退耕还林、还草的政策，劳动力外出打工等导致粮食种植面积有所减少；但由于国内外粮油价格、科技技术进步和农业生产力发展，粮食单产有所提高，这样粮食总产量会维持在5亿吨以上，这证明本模型的预测结果符合我国粮食产业发展趋势。

表2 各种模型对1978―2000年粮食产量的拟合值 万吨

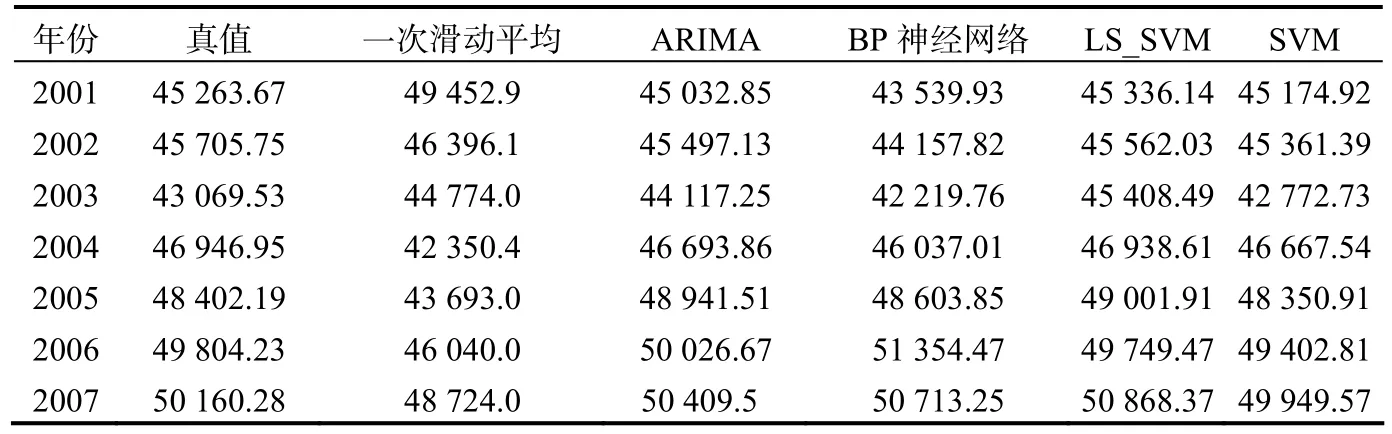
表3 各种模型对2001―2007年粮食产量泛化值 万吨

表4 2008―2010我国粮食产量的预测值

表5 各种模型RMSE和MAPE比较

四、结论

粮食产量序列数据具有非线性特征，存在弱混沌特性，因此采用精确的数学模型预测比较困难。支持向量机适合于小样本的粮食产量建模与预测，而对模型的定阶方法进行改进后，可以较好地拟合粮食产量时间序列模型，获得较高的回归与建模精度，其外推预测也具有较高的泛化能力。由于粮食生产是自然再生产与经济再生产的统一，粮食产量预测是受政策、自然环境、资源投入等多因素的影响，本文没有考虑到这些因素的影响，只考虑粮食产量历史数据，这是今后要进一步研究的方向。

[1]陈成忠，林振山.山东省粮食产量波动的多时间尺度分析[J].农机化研究，2007(10)：1-4.

[2]张晓杰，张希良.时间序列分析模型在山东省粮食总产量预测中的应用[J].水土保持研究，2007，14(3)：309-311.

[3]吕效国，王晓燕，孙建平，吴梅君.用自回归预测的新方法预测粮食产量[J].安徽农业科学，2008，36(33)：14359-14374.

[4]王启平.BP神经网络在我国粮食产量预测中的应用[J].预测，2002，21(3)：79-80.

[5]禹建丽，黎 娅.基于人工神经网络的粮食产量预测模型[J].河南农业科学，2005(7)：44-46.

[6]Vapnik V.The nature of statistical learning theory[M].New York：Springer-Verlag，2000.

[7]刘 涵，刘 丁，李 琦.基于支持向量机的混沌时间序列非线性预测[J].系统工程理论与实践，2005(9)：94-99.

[8]曲文龙，樊广佺，杨炳儒.基于支持向量机的复杂时间序列预测研究[J].计算机工程，2005，31(23)：1-3.

[9]罗正根.机器学习新方法：支持向量机[J].湖南农业大学学报：社会科学版，2009(2)：111-114.

[10]李晓东，席升阳，潘 立.基于最小二乘支持向量机的中国粮食产量预测模型研究[J].水土保持研究.2007，14(6)：321-324.

[11]任勋益，王汝传，谢永娟.基于支持向量机和最小二乘支持向量机的入侵检测比较[J].计算机科学，2008，35(11)：83-85.

[12]阎威武，邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究[J].控制与决策[J]，2003，18(3)：358-360.

[13]袁哲明，张永生，熊洁仪.基于 SVR的多维时间序列分析及其在农业科学中的应用[J].中国农业科学，2008，41(8)：2485-2492.

[14]Kim H S，Eykholt R J D.Salas.Nonlinear dynamics，delay times and embedding windows[J].Physica D，1999(127)：48-60.

Study on the support vector machines model of grain production prediction

XIANG Chang-shenga,ZHOU Zi-yingb,WU Li-nab

(a.College of Orient Science & Technology; b.College of Resources & Environment,Hunan Agricultural University,Changsha 410128,China)

The grain production is complicated and unpredictable.In attempting to predict time series data,statistical methods are the major research stream in tradition,however,the factor of time is often overlooked in tradition model.In this paper,a model with multi-input and single output was proposed based on improved support vector machines(SVM)using leave one out for cross validation.China grain production data sets are predicted using this method; the results show that the SVM predictor has higher precision and greater generalization ability.

grain; production prediction; support vector machines; time series

F323.5

A

1009-2013(2010)01-0006-05

2009-11-16

“十一五”国家科技支撑计划(2008BADA 4B108)

向昌盛(1971─)，男，湖南怀化人，副教授，博士，主要从事计算数学、智能预测研究。

李东辉