基于卡诺图在处理逻辑函数方面的应用研究

徐 兵 朱鹏远

(1,2.昌吉学院物理系 新疆 昌吉 831100)

基于卡诺图在处理逻辑函数方面的应用研究

徐 兵1朱鹏远2

(1,2.昌吉学院物理系 新疆 昌吉 831100)

卡诺图是数字电路逻辑设计中必不可少的工具,它在逻辑函数的处理方面有着较多的应用,如简化函数、逻辑运算、形式转换等。很好地利用卡诺图所具有的功能,可以使逻辑电路的设计方案达到最佳。

卡诺图;逻辑函数;原变量;反变量

1 引言

卡诺图是数字电路逻辑设计中必不可少的工具,其基本用途是对逻辑函数进行简化,但它还有很多被人们开发出来的其它用途。在逻辑电路的设计中,常常要求使用个数及种类均较少的逻辑器件来实现特定的逻辑功能,这就必须对已知的逻辑函数进行适当的处理才能够达到目的,满足设计要求。本文就卡诺图在处理逻辑函数方面的应用做一些探讨性的研究。

2 卡诺图用于逻辑函数的化简

逻辑函数主要有两种表示方法:逻辑函数表达式和卡诺图,在对逻辑函数进行化简和运算时,应用卡诺图相对比较简单直观,而且不需要套用很多的定理和公式,易于掌握。当函数包含的变量个数不太多时,用卡诺图进行逻辑函数的化简和运算显得尤其方便,这也是卡诺图的最基本的应用。

2.1 逻辑函数的卡诺图表示

卡诺图的一个重要的特征是能够在图形上直观地反映最小项的相邻关系,它将逻辑函数所涉及的n个变量分为两组,两组变量均按照循环码排列,构成一个二维表格。其中,每一个小格对应于逻辑函数的一个最小项,二维表格恰好包含了 n变量的逻辑函数的全部最小项。当函数的变量取值与某小方格代表的最小项相同时,函数值为1,小方格中也就对应地填入 1。因此,对于任意一个“与—或”逻辑表达式,只要充分利用AB+=A的关系,就可以快速地将逻辑函数填入卡诺图中。如:将 F=AC+用卡诺图表示出来。该函数涉及四个变量A、B、C、D,对于第一个“与”项AC,它在卡诺图中对应的小方格的集合为 A=1,C=1的所有小方格的集合,即:{m10,m11,m14,m15},不必考虑B、D的取值情况;第二个“与”项在卡诺图中对应的小方格的集合为 A=1,B=1,C=0的所有小方格的集合,即:{m12,m13},不必考虑D的取值;第三个“与”项在卡诺图中对应的小方格的集合为 A=1,B= 0,D=1的所有小方格的集合,即:{m9,m11},不必考虑 C的取值。第四个与项在卡诺图中对应的小方格的集合为A=0,B=0,D=1的所有小方格的集合,即:{m1,m3},也不必考虑 C的取值;用这种方法可以快速地得到逻辑函数的卡诺图表示结果,如图 1所示。

2.2 用卡诺图化简逻辑函数

①将卡诺图中 2n个相邻的“1”格画在一个矩形圈内(即卡诺圈);

②圈内“1”格要尽量地多;图上表征逻辑函数取值为 1的相邻最小项的相邻小方格进行合并,达到以简单的一个“与”项替代若干个最小项的目的。

卡诺图变量取值组合按循环码的规律排列,使处在相邻位置的最

③每个“1”格可以被重复圈用;

④每个“1”格必须至少被圈过 1次;

⑤每个圈中至少有一个从未被圈过的”1”格;

⑥卡诺圈的个数要最少。

写出最简“与—或”逻辑表达式的方法:一个卡诺圈写 1个“与”项,将圈中没有发生 0、1变化的变量相乘即可。其中,始终为 1的变量写为原变量,而始终为 0的变量写为反变量。然后将所有与项相加,就获得了逻辑函数的最简“与—或”表达式。如图 2所示,按照圈“1”规则,可画得三个卡诺圈,因此最简“与—或”逻辑表达式为:

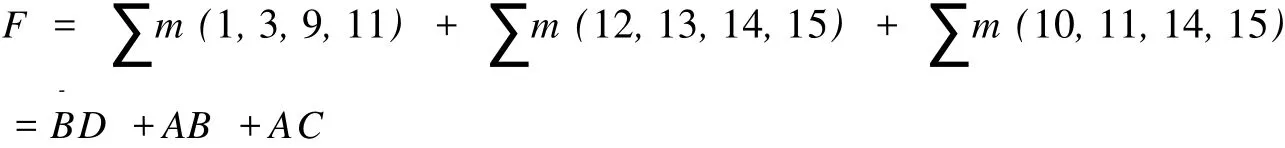
3 用卡诺图获得逻辑函数的反函数和对偶函数

3.1 用卡诺图获得逻辑函数的反函数最简“与—或”式

原函数的卡诺图中的“0”格所对应的最小项即为反函数所对应的最小项。将它们按照圈“1”格的规则进行操作,即把相邻的 2n个“0”格圈为一个卡诺圈,将其中对应的没有发生 0、1变化的变量相乘,作为一个“与”项。其中,始终为 1的变量写为原变量,而始终为 0的变量写为反变量。照此把所有的卡诺圈完成后,将所得的各个“与”项相加,既得逻辑函数的反函数的最简“与—或”表达式。如我们将图 1所示的逻辑函数的“0”格全部标出,并画出卡诺圈,如图 3。则反函数的最简“与—或”形式为:

3.2 用卡诺图获得逻辑函数的对偶函数最简“与—或”式

首先,由原函数的卡诺图获得其反函数的全部最小项编号 (即原函数卡诺图中的 0格所对应编号)。那么对偶函数中的最小项与反函数中的最小项一一对应,其关系为:若反函数中最小项编号为 i,则对偶函数中有编号为 (2n-1)—i的最小项 [n为函数变量个数 ][3]。由此获得对偶函数的全部最小项,填出对应的卡诺图,然后进行圈“1”格的操作,即可写出对偶函数的最简“与—或”表达式。如我们

对图 1所示的逻辑函数求对偶函数,过程如下:由原函数的卡诺图可知反函数的全部最小项编号为{0,2,4,5,6,7, 8},则可得对偶函数的全部最小项的编号应该是{15,13,11,10,9,8,7},

画出对应的卡诺图如图 4,进行圈“1”格的操作,得对偶函数最简“与—或”式为:

4 用卡诺图实现逻辑函数不同表示形式之间的转换

在数字逻辑设计运算中,最基本的逻辑运算是“与”、“或”、“非”三种运算,通过这三种基本运算逻辑函数可表示成许多不同的形式,常见的有“与—或”式、“或—与”式、“与非—与非”式、“或非—或非”式、“与—或—非”式等五种形式。利用卡诺图可以很方便地实现逻辑函数在这五种形式之间转换,方法简单,不易出错。

逻辑函数的最简“与—或”式的获得方法已在 2.2中细说,这里就不再举例说明了。

4.1 将逻辑函数转换为“或—与”式

将逻辑函数填入卡诺图中,然后按照圈“1”格的方法,对卡诺图中的“0”格画出卡诺圈,如图 3。一个圈写 1个“或”项,将卡诺圈中没有发生 0、1变化的变量相加即为“或”项。其中,始终为 1的变量写为反变量,而始终为 0的变量写为原变量。然后将各“或”相相乘,既得逻辑函数的最简“或—与”式。如我们写出图 1所示的逻辑函数的最简“或—与”式:

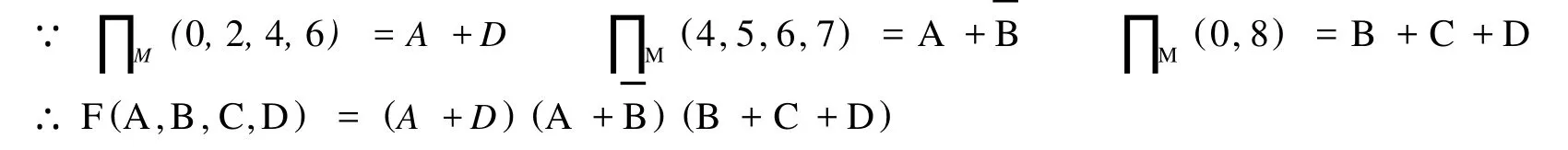
4.2 将逻辑函数转换为“或非—或非”式

要获得逻辑函数的“或非—或非”式,只需要将所获得的“或—与”式利用 F=和

进行变换即可。如对 4.1中获得的“或—”与式进行变换可得“或非—或非”式:

4.3 将逻辑函数转换为“与—或—非”式

要获得逻辑函数的“与—或—非”式,只要求出其反函数的最简“与—或”式,然后对等式两边再求一次反即可。我们写出图 1所示的逻辑函数的“与—或—非”式:

5 结束语

在设计实际的数字系统时,为了减少所用器件的数目,往往不限于使用单一逻辑功能的门电路,这时希望得到的最简逻辑式可能既不是单一的“与—或”式,也不是单一的“与—非”式,而是一种混合的形式。因此,究竟将函数化简、变换成哪种形式最为有利,还要根据选用哪些种类的电子器件而定[4]。通过探究,我们更加充分地了解了卡诺图在处理逻辑函数方面的应用,为选用器件的种类提供了方便。

[1][4]闫石.数字电路技术基础(第四版)[M].北京:高等教育出版社,1998.

[2]华成英.数字电路技术基础[M].北京:高等教育出版社,2002.

[3]王毓银.数字电路逻辑设计(第三版)[M].北京:高等教育出版社,1999.

TN702

A

1671-6469(2010)03-0096-03

2010-05-21

徐兵 (1956-),女 ,甘肃民勤人,昌吉学院物理系,副教授,研究方向:电工、电子技术理论与实践的教学与研究。

(责任编辑:代琴)