热力学函数及麦氏关系的简便记忆法

张保花 王 伟 郭福强

(1,2,3.昌吉学院物理系 新疆 昌吉 831100)

热力学函数及麦氏关系的简便记忆法

张保花1王 伟2郭福强3

(1,2,3.昌吉学院物理系 新疆 昌吉 831100)

本文主要通过引入热力学状态函数,推导出相应的全微分方程,从中找出规律,类比推出麦氏关系。通过引入图表,详细论述记忆麦氏关系的简便方法,它有助于学生对麦氏方程的深刻理解,克服难以记忆、容易出错等多种现象,以便学生能得心应手地应用此方程。

状态函数;麦氏关系;简便记忆法

1 引言

《热力学统计物理》中热力学部分的核心是基本的热力学函数及相应的微分方程、麦氏关系,并将其应用于热力学实际问题,同时它也是教学的重点和难点[1]。就教师教学过程而言,存在许多困难,如概念的引入和多种热力学函数的比较等很抽象,难以使学生直观的理解;就学生掌握情况而言,由于概念和热力学函数较多、微分表达式的变量较复杂,使学生掌握的知识很容易混淆。所以,本文从热力学函数的引入出发,给出热力学函数相应的微分表达式,后推导出麦氏关系,给学生一个清晰地推理过程,从以上内容中总结规律,提出比较简单的记忆方法,提高学生的记忆准确率,使其能够更好的应用解决实际问题。

2 热力学函数的引入

根据热力学的基本规律引入三个基本的热力学函数,物态方程、内能和焓,并导出了热力学的基本方程[2]:

上式给出的是相邻两个平衡态的内能、熵、体积的增量之间的关系,不论是通过可逆过程还是不可逆过程从一平衡态到达另一平衡态,上式都是成立的。因此可以把上式理解为 U作为 S、V函数的全微分表达式。

2.1 焓 (H)的引入

一个系统在某一过程中温度升高 1K所吸收的热量,称作系统在该过程的热容量。以△Q表示系统在某一过程中温度升高△T所吸收的热量,则系统在该过程的热容量 C为

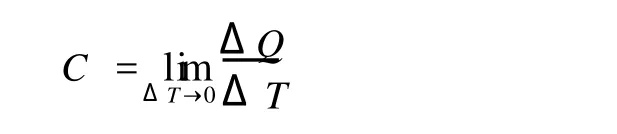
在实际问题中,经常用到系统在等容过程和等压过程的热容量,分别以 CV和 Cp表示。在等压过程中,外界对系统所作的功W=-P△V,带入到热力学第一定律的数学表达式中得:Q=△U+P△V。所以

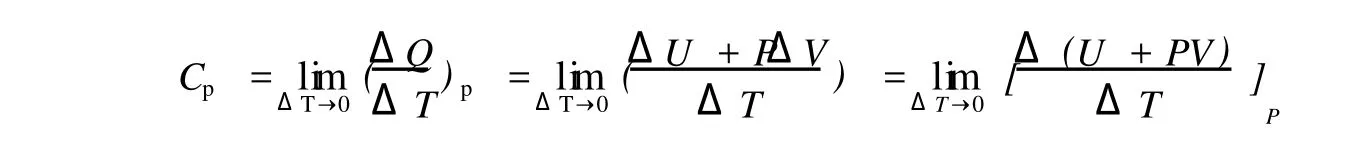
现在引入一个状态函数 H,名为焓:H=U+PV

根据焓 (H)的定义,若将 PV理解为系统抵抗外压所具有的能量—外能 Qp,则焓可理解为内能与外能之和,即系统的总能量。

2.2 自由能 (F)的引入

根据热力学第二定律的数学表达式,指出对于绝热系统可以用熵函数判断系统中可能发生的变化。不过在实际应用上,对于某些经常遇到的物理条件,用其它热力学函数进行判断更为方便。如遇到约束在等温条件下的系统,设系统由初态 A经过等温过程到达终态 B,由热力学第二定律数学表达式可知[3]:

式中等号适用于可逆过程,不等号适用于不可逆过程。

根据热力学第一定律,UB-UA=Q+W,带入到上式中得:

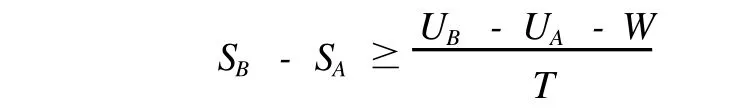
整理得:UB-UA-T(SB-SA)≤W,即ΔU-TΔS≤W

在等温条件下有:Δ(U-TS)T≤W

引入一个新的态函数,名为自由能:F=U-TS

则上式可改写为:

上式表明在等温过程中,系统对外界的功 -W不大于自由能的减少,换句话说,系统的自由能的减少是在等温过程中从系统所能获得的最大功。这个结论称为最大功定理。

根据最大功定理及自由能 (F)的定义式,F可理解是内能中可自由转化为做功的那一部分能,TS是不能转化为做功的能量,称为束缚能。这是 F称作自由能的原因。

2.3 吉布斯函数的引入

在实际问题中也往往遇到约束在等压条件下的系统。在等压过程中外界对系统所做的体积变化的功是 -P(VB-VA),如果除体积变化的功外,还有其它形式的功W1,则在过程中外界对系统所做的总功为

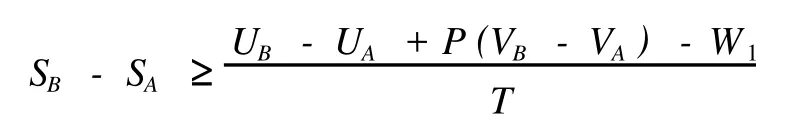
上式整理得:UB-UA-T(SB-SA)+P(VB-VA)≤W1

在等温等压条件下有:Δ(U-TS+PV)≤W1

引入新的状态函数,名为吉布斯函数 G:

则上式可改写为ΔG=GB-GA≤W1,或改写为:GA-GB≥-W1

上式表明:在等压过程中,除体积变化功外,系统对外所做功不大于吉布斯函数的减少。换句话说,吉布斯函数的减少是在等温等压过程中,除体积变化功外从系统所能获得的最大功。

因为 H=U+PV,所以吉布斯函数又可写为 G=H-TS,它与 F与 U的关系类似,G又称为自由焓,即总能量中可自由转化为做功的那一部分能量。

3 热力学函数的全微分及麦氏关系

可以把上式 (1)理解为 U作为 S、V的函数的全微分表达式,表达式为:

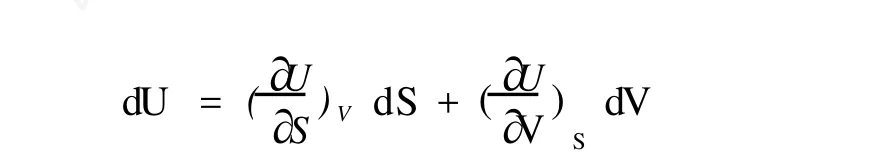
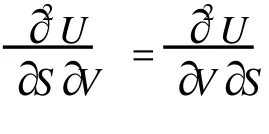
我们从焓的定义:H=U+PV出发,求焓的全微分式时,将热力学基本方程:dU=T dS-P dV代入得焓的全微分式为:

可将焓 H看成 S、P的函数,S、P为自变量,全微分表达式可表示为:

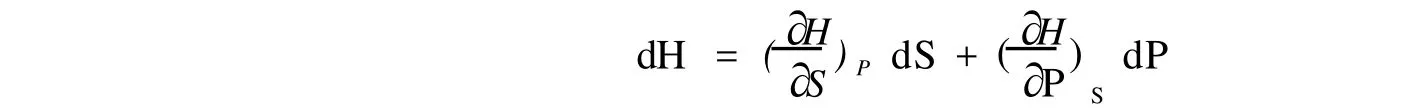
类似的考虑到完整全微分条件:

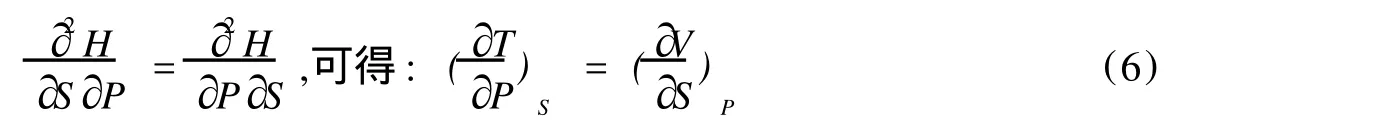
由自由能的定义:F=U-TS出发,求自由能全微分式时,将热力学中内能的全微分式 dU=T dSP dV代入得全微分式为:dF=-SdT-PdV

可将 F看成是 T、V的函数,自变量为 T、V,则自由能的全微分表达式写为:

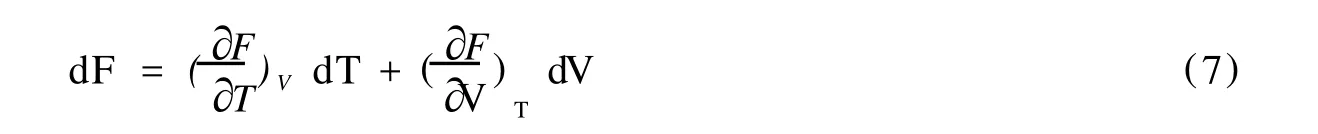
类似的考虑到完整微分条件:

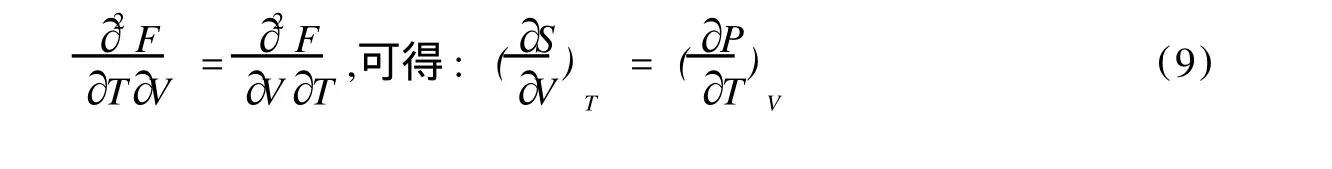
从吉布斯函数 G的定义:G=U-TS+PV出发,求吉布斯全微分式时,将热力学中内能的全微分式dU=T dS-P dV代入得全微分式为:

可将 G看成是 T、P的函数,自变量为 T、P,则自由能的全微分式写为:

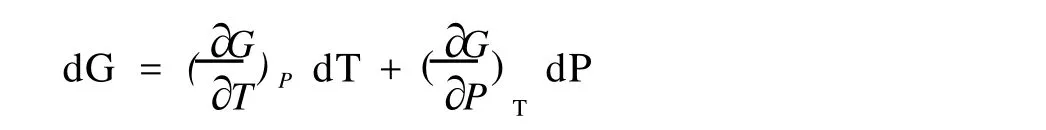
类似的考虑完整微分条件:

(1)(4)(7)和 (10)四式是四个基本热力学函数的全微分式,(2)(5)(8)和 (11)四式将 S、T、P、V四个变量用热力学函数 U、H、F、G的偏导数表达出来,同时 (3)(6)(9)和 (12)四式则给出 S、T、P、V四个变量的偏导数之间的关系,它们最初是由麦克斯韦导出的,故称为麦氏关系[5]。

4 热力学函数及其全微分表达式的简便记忆法

通过对以上知识的归纳总结,首先从三种函数定义出发[6],可以看出其自变量是由 P、V、T、S任意两个组合构成的,如 U(S,V),H(S,P),F(T,V),G(T,P)。为了能更快地记忆状态函数和相应的自变量,从图 1中可以看出四个自变量位居四个顶角处,状态函数 G、H、U、F分别放在第一、二、三、四象限中。状态函数相应的自变量为临近的两个顶角的变量,如与U临近的两个顶角处的自变量为 S、V,故 U的自变量为 (S、V);与 F临近的两个顶角的自变量为 T、V,故 F的自变量为 (T、V);与 G临近的两个顶角的自变量为 P、T,故 G的自变量为 (P、T);与 H临近的两个顶角的自变量是 S、P,故 H的自变量为 (S、P)。

在书写状态函数及自变量的全微分表达式时,箭头出发处变量微分符号为正“+”,箭头终点处变量微分符号为负“—”。如 dS为箭头出发处为“+”,TdS故“+”,dV为箭头终点处为“—”,故 PdV为“—”则U的全微分表达式为 dU=T dS-P dV;相应的 dS、dP均为箭头出发处,则VdP、TdS均为“+”,则 H的全微分表达式为 dH=T dS+V dP;类似 dT、dV均在箭头终点处则为“—”,故 SdT、PdV均为“—”,则 F的全微分表达式为 dF=-SdT-PdV;dP位于箭头出发处为“+”,故 VdP为“+”,dT处于箭头终点处为“—”,故 SdT为“—”,相应的 G的全微分表达式 dG=-SdT+V dP。

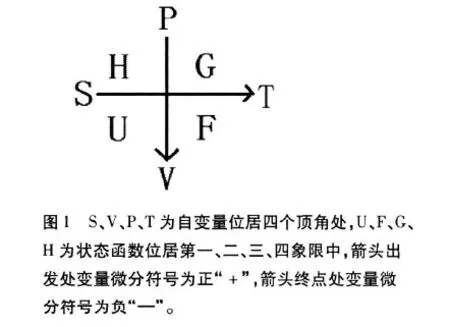
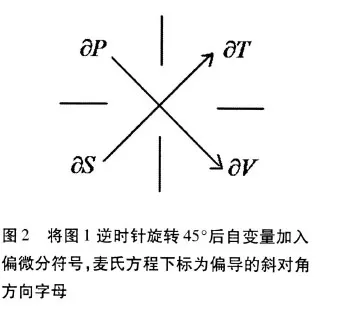
5 麦氏关系的简便记忆法

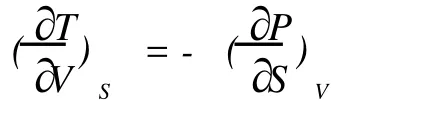
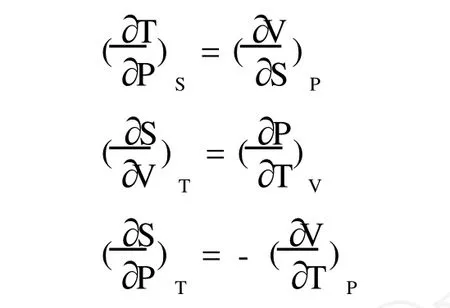
图 2是由图 1逆时针旋转 45°后,自变量加入偏微分符号,状态函数换为分数符号“—”,可以认为为分子或分母,麦氏关系的下标为分子偏导数的斜下对角方向字母,分子偏导数位于箭头出发处为“—”,分子偏导数位于箭头终点处为“+”[8]。如为分子、为分母时分式为位于箭头出发处为“—”,分式的右下标为分子偏导数的斜下方向字母 V,故为 -,它等于分子位于箭头终点处的分式,故为正值,即

[9];类比可知以为分子,以为分母的分式,下表为分子偏导数的斜下方字母 T,又因 5S位于箭头出发处则为“—”,即为 -,它等于分子为位于箭头终点出的分式,即=-;依次类推快速的推导出其它两组麦氏关系[10]表达式:

总之,通过热力学函数的引入,给出了相应的微分表达式,从而推导出麦氏关系,进一步总结归纳出记忆热力学状态函数及微分表达式、麦氏关系的简便记忆法,使学生们比较轻松地学习,记忆更加深刻,能够更准确地应用于解决实际问题。

[1] [2]阿力甫·沙吾提.开放热力学系统麦氏关系的讨论[J].新疆师范大学学报 (自然科学版),2007,26(4):51-54.

[3] 汪志诚.热力学统计物理 (第三版)[M].高等教育出版社,2005:71-74.

[4][5] 王竹溪.统计物理学导论 (第二版)[M].高等教育出版社,1982:65-69.

[6] 杨海莲,邹艳.图形记忆法—几个热力学关系的记忆规律讨论[J].榆林学院学报,2007,17(6):41-43.

[7] 刘玉兰.几种推导麦氏关系的方法[J].淮坊学院学报,2005,5(6):105-106.

[8] Reif,F.Fundamentals of Statistical and Ther mal Physics[M].McGraw-Hill Book Company,1965.

[9] 龚昌德.热力学与统计物理学[M].高等教育出版社,1982:80-83.

[10] 汪志诚.热力学统计物理 (第二版)[M].高等教育出版社,2001:87-89.

O414.11

A

1671-6469(2010)03-0103-05

2010-01-04

昌吉学院研究生启动课题 (09SSQD021)

张保花 (1981-),女,昌吉学院物理系,讲师,研究方向:纳米材料的热动力。

(责任编辑:代琴)