对离差的几点认识和思考

陈香莲 李 燕

(1,2.昌吉学院数学系 新疆 昌吉 831100)

对离差的几点认识和思考

陈香莲1李 燕2

(1,2.昌吉学院数学系 新疆 昌吉 831100)

空间解析几何课程中,离差是空间平面部分的一个教学难点,由于离差不是本课程的主要基本概念,故许多初学者均没有给予充分的认识。本文对“离差”作一些简单的探讨,希望对初学者有一定的帮助。

离差;解析几何

0 点与平面的离差概念

定义 1[1]:如果自点M0到平面π引垂线,其垂足为 Q,那么向量平面π和单位向量的射影叫做点M0与平面π间的离差,记做δ=射影 1所示)。

图1

特别的,当平面π过原点 O时,取以原点 O为始点与平面π垂直的任一个单位向量作为单位法向量于是,当,有δ >0;当,有δ<0;当点M0∈π即点M0在平面π上时 ,有δ =0。

1 引进“离差”概念的必要性

《解析几何》(吕林根)教材中,在讨论点与平面的位置关系时引入了“离差”的概念,并且“离差”与点与平面的距离有密切联系。显然,离差的绝对值,就是点M0与平面π间的距离 d。但是,点到平面的“距离”只能刻画点到平面的远近,而不能区分两点在平面的同侧还是异侧。为了判断点与平面的位置关系,“离差”的引进就很有必要;并且,利用“离差”还可以解决平面划分空间的问题,同时给出了三元一次方程的几何意义[3]。

2 离差的应用

由离差的定义,利用离差可以方便的解决以下相关的几何问题。

2.1 判断两点在同一平面的同侧还是异侧

例 1求点M(1,2,3)和平面 2x-2y+z-3=0的离差和距离。

在定义 1中,平面π不过原点 O,则当 向,即点M0与原点在平面π异侧时,有δ>0;当向,即点M0与原点在平面π同侧时,有δ<0;当点M0∈π即点M0在平面π上时,有δ=0。于是,我们可以判断两点在同一平面的同侧还是异侧。

例 2 确定点 p1(1,2,3)和 p2(2,1,5)相对于平面 5x-6y+z-5=0的位置。

解设F(x,y,x)=5x-6y+z-5,

因为F(1,2,3)=5-12+3-5<0,F(2,1,5)=10-6+5-5>0

所以点 p1(1,2,3)和 p2(2,1,5)在平面 5x-6y+z-5=0的两侧。□

解此题的关键是掌握“离差”的意义:对于平面π同侧的点,δ的符号相同;对于平面π异侧的点,δ的符号相反。另外,在解题方法上,因只是考虑符号问题,故不必求出δ的具体值,只需判断其符号即可,简化运算量。

2.2 求两平面所组成的二面角的平分面

显然,这样的平分面有两个。从距离的角度都满足 d1=d2的几何条件,只有运用离差的概念才能把它们区分开,其中一平分面满足条件δ1=δ2,另一平分面满足δ1=-δ2。

例 3试求由平面π1:2x-y+2z-3=0和π2:3x+2y-6z-1=0所构成的二面角的角平分面的方程,在此二面角内有点M(1,2,-3)。

分析:二面角的角平分面有两个。设 P(x,y,z)为角平分面上任意一点,设点 P到π1的距离 d1=p,到π2的距离 d2;则点 P到π1的离差δ1=±p,到π2的离差δ2。因为 P点与M点在同一个二面角内,因此 P点与平面π1和π2离差的符号与点M与平面π1和π2离差的符号情况相同。

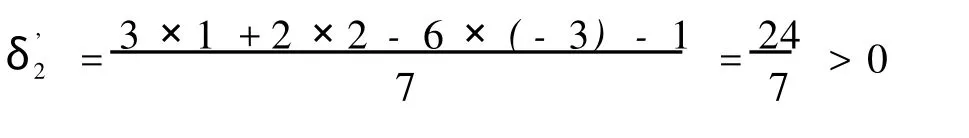
设 P(x,y,z)为所求角平分面上任意一点

化简得:23x-y-4z-24=0,即为所求的角平分面的方程。□

解题的关键是因为 P点与M点在同一个二面角内,因此 P点与平面和离差的符号与点M与平面和离差的符号相同。这正是引入“离差”的意义所在。

解 (1)化π1和π2的方程为法式方程

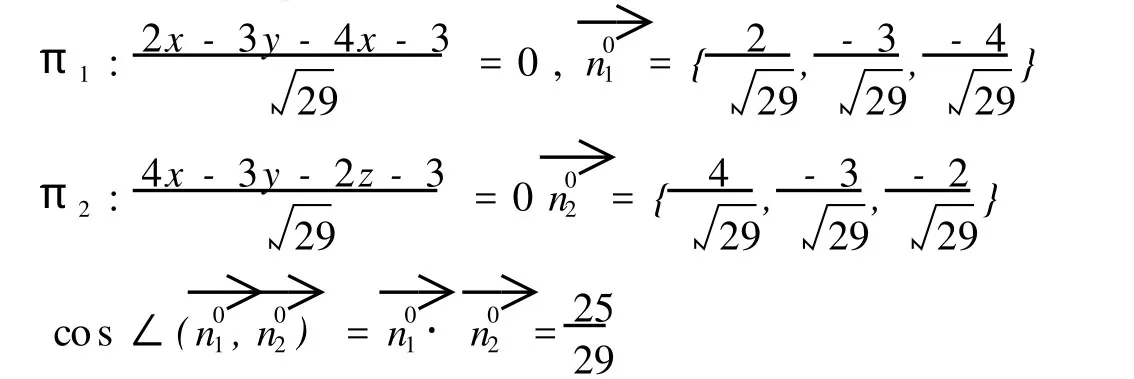
(2)设 P(x,y,z)是含原点的二面角的平分面上任意一点。则有点 P与平面的离差δ1=;点 P与平面的离差δ2=;又因为点 P与原点在同侧,点 P与原点在同侧 故δ1=δ2;即

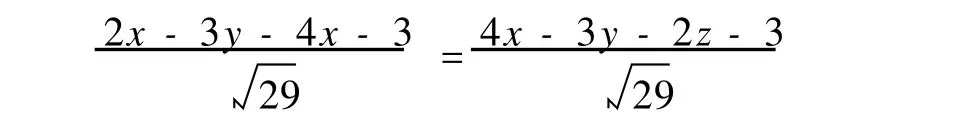
化简得:x+z=0,即为所求的钝角平分面的方程。

(3)设 p(x,y,z)是不含原点的二面角的平分面上任意一点。同理分析可得δ1=-δ2;即

化简得:x-y-z-1=0,即为所求的锐角平分面的方程。□

3 小结

以上我们仅仅列举了利用“离差”解决的部分几何问题,但利用“离差”可以解决的几何问题还有很多,例如,利用“离差”,我们还可以判断给定两点M和 N在由两相交平面所构成的同一个二面角内,还是分别在相邻的二面角内,或是在对顶的二面角内?关于此方面的应用可参见文献[4]。总之,在学习中充分理解“离差”概念及其几何意义,善于灵活运用,便可有效的解决许多相关的几何问题。

[1][2][3] 吕林根,许子道等.解析几何 (第四版)[M].北京:高等教育出版社,2006.

[4] 杨文茂,李全黄.空间解析几何习题集[M].武汉大学出版社,2003:83-84.

O182.2

A

1671-6469(2010)03-0093-03?

2010-04-13

昌吉学院研究生科研启动基金项目(09SSQD019)

陈香莲 (1965-),女,安徽濉溪县人,昌吉学院数学系,副教授,研究方向:基础数学及图论及其应用。

(责任编辑:代琴)