低刚度铣削工艺系统的弹性铣削力建模方法

戚厚军 ， 张大卫，蔡玉俊，沈 煜

(1. 天津大学机械工程学院，天津 300072；2. 天津工程师范学院天津市高速切削与精密加工重点实验室，天津 300222)

在航空、军工、能源、船舶等国家重点发展行业中，薄壁类零件的切削加工是非常常见的加工工艺．而该类零件一般具有形状复杂、难切削、切削力复杂、极易产生加工形变、失稳和振动等问题，使得加工完的零件易发生弯曲、扭曲或弯扭组合等形变，很难控制零件的加工精度，严重影响产品的性能，长期以来一直成为加工领域中公认的难题，受到业内人士的广泛关注．为此很多学者关注加工误差的预测研究[1-11]，其中关键技术在于铣削力的合理建模，而低刚度工艺系统的形变预测则是铣削力建模的基础．大量的铣削力模型中形变预测研究多集中在两方面：一是将刀具等效为悬臂梁结构[1-6]；二是采用FEM 方法预测工件的铣削形变 ．由于处理工件形变的数据繁杂，所以长期以来 FEM 方法在工程中一直未得到广泛应用．为此，笔者结合薄壁立板的高速铣削过程，基于弯扭剪耦合弹性力学理论，推导出了工件弹性铣削形变的解析式，计算出工件任意点的铣削形变；同时考虑到工件和铣刀的弹性形变共同引起铣削啮合角的变化，推导出啮合角的表达式；建立了低刚度工件-刀具工艺系统的弹性铣削力模型．该研究为提高高速铣削薄壁构件的加工精度提供了理论依据和方法．

1 工件-刀具系统的形变分析

在机床-夹具-工件-铣刀组成的铣削加工系统中，周铣薄壁工件时，法向的水平分力 Frj是引起铣削形变的主要原因，因此，针对低刚度工件-刀具系统，铣削加工系统的形变可表示为

式中：δwy为 y 方向(法向)工件受力产生的形变量；δcy为y 方向(法向)刀具受力产生的形变量．

1.1 工件弹性铣削形变

低刚度工件受到铣削力的作用后，产生弹性铣削形变，如图1 所示，其形变主要为铣削分力Frj产生的弯扭剪耦合形变，形变表达式为

式中：δMy为弯矩产生的形变量；δFy为横向力产生的形变量．

距离工件夹持面高度为 zh处，作用法向铣削力Frj，使得工件产生弯扭形变，根据弯扭弹性形变原理，推导出立板的弯扭铣削形变为

式中：h 为工件高度；E′ 为工件(板)的弹性模量；μ 为泊松比；E 为拉伸弹性模量；s 为工件厚度；w 为工件长度，w=w1+x；G 为工件剪切模量．

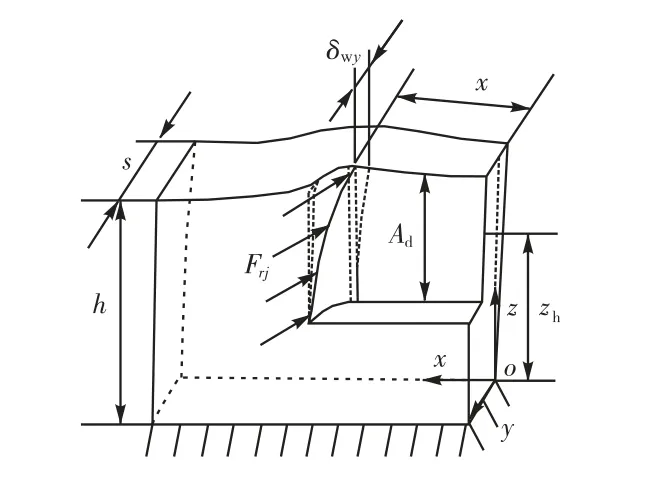
图1 工件铣削形变示意Fig.1 Part milling deflection

同时，作用于工件上的法向铣削力 Frj，使得工件产生横向力形变，根据剪切弹性形变原理，推导出立板的剪切铣削形变为

1.2 刀具弹性铣削形变

刀具夹持在机床的夹头上，可将刀具等效为悬臂梁结构．当受到铣削分力 Fτj、Frj的作用后，刀具在 x方向(切向)和 y 方向上的弯曲形变分别为 δcx和δcy．由于刀具由刀柄和刀刃两部分组成，而刀柄和刀刃的弯曲刚度不同，因此，其弹性铣削形变[1]为

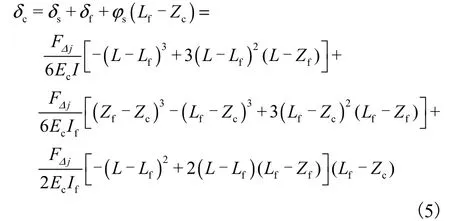
式中：δs为刀柄部分形变量；δf为刀刃部分形变量；φs为刀柄部分形变角；FΔj为铣削分力 Fτj和 Frj；Lf为刀刃长度；L 为刀具悬臂长度；Zc为铣刀上形变点距刀具底端处的距离；Zf为铣削力作用点到刀具底端处的距离；I 为刀柄部分的惯性矩；If为刀刃部分的惯性矩；Ec为刀具弹性模量．

2 弹性铣削力建模

薄壁结构件的铣削力与铣削加工工艺系统的动态弹性形变密切相关，并呈非线性．在弹性铣削力模型中，铣削力使得低刚度工件-铣刀偏离了理想的切削位置，从而使未形变切屑厚度发生变化；该变化又反馈给切削系统，形成新的铣削力；而新的铣削力又引起新的铣削形变和新的瞬时铣削厚度的变化，最终铣削力与铣削形变达到平衡状态．因此，工件-铣刀系统的弹性形变是弹性铣削力预报的基础．该弹性形变量主要影响到铣削力的啮合角和瞬时切削厚度．下面从工件-铣刀切削形变对切削路径影响的几何关系出发，研究切削微单元的瞬时切削厚度与切削位置角的变化，建立低刚度铣削工艺系统的弹性铣削力模型．

2.1 切削啮合角分析

如图2 所示，将圆柱铣刀的铣削刃离散为n 个切削微单元的集合，铣刀的螺旋角为 λ，切削刃数为 Nf，刀具半径为 R，每个微单元的名义高度为 dz=Ad/n(Ad是轴向切深)，设 θ(j)为铣刀的初始位置角，当铣刀刃位于第 j 个转角时，φ(i)为第 i 个微单元与第 k 个刀尖之间的夹角在刀具端面上的投影，则第k 个刀刃上第j 个初始位置第i 个微单元的切削角为

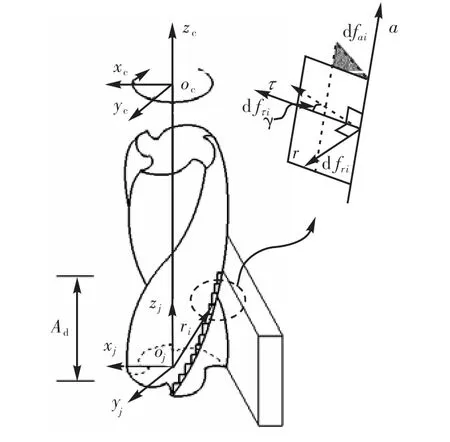
图2 刀具铣削力模型Fig.2 Cutter milling force model

在铣削过程中考虑到工件(刀具)的弹性形变，第i 个单元的实际高度为

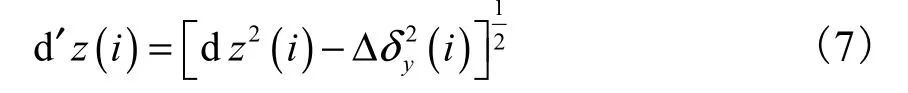
式中Δδy(i)为第i 个单元在y 方向上的相对形变量，即

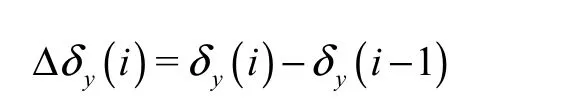
当刀具沿着x 方向进给铣削薄壁件时，作用在薄壁件上的切向、法向和轴向切削力分别为 Fτ(φ)、Fr(φ)和 Fa(φ)．若工件为弹性体，刀具为刚性体时，刀具与工件之间未变形的切削面积为 ABC；若工件、刀具均为弹性体时，切削面积变为 A′B′C′，如图 3 所示．由于刀具发生了弹性形变，其轴线的中心位置由o′j变化为位置 oj，刀具铣刀刃上位于第 j 个转角时切削啮合角相应发生了变化，刀刃上的切削啮合角变为

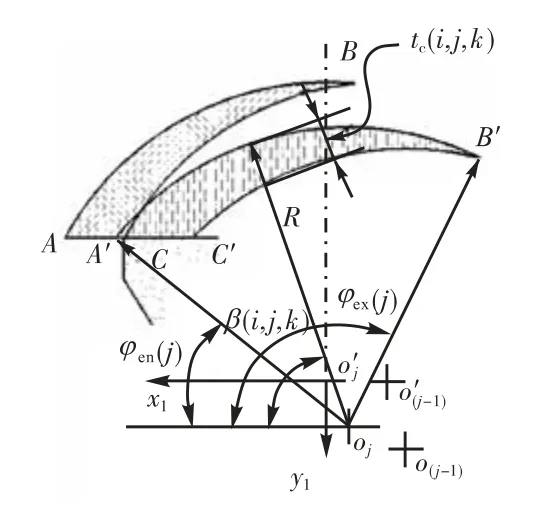
图3 弹性系统瞬时切削厚度Fig.3 Chip thickness for flexible process

其中，刀刃上的切入角为

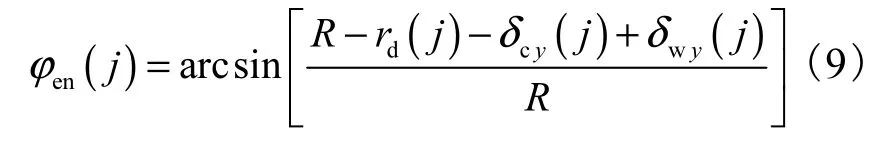
式中：rd(j)为刀具名义径向铣削深度；δwy(j)为铣削位置处工件的法向形变量；δcy(j)为铣削位置处刀具在y方向上的形变量．

而刀齿的切出角为

式中：δcx(j-1)、δcx(j)为刀具在 j、j-1 位置x方向上的铣刀形变量；δcy(j-1)、δcy(j)为刀具在 j、j-1 位置 y 方向上的铣刀形变量；ft为每齿进给量．

2.2 瞬时切削厚度分析

随着工件-刀具弹性铣削形变的不同，切屑微单元的瞬时切削厚度随之变化．如图 3 所示，在切削刃转角为 β(i，j，k)时，第 k 个铣削刃第 i 个微单元的瞬时切削厚度为

其中

2.3 弹性铣削力计算

对于铣刀刃上的任一微单元，切削机理为斜角切削．作用在微单元上的切向力 dfτi(φi)、法向力 dfri(φi)和轴向力dfai(φi)可表示为

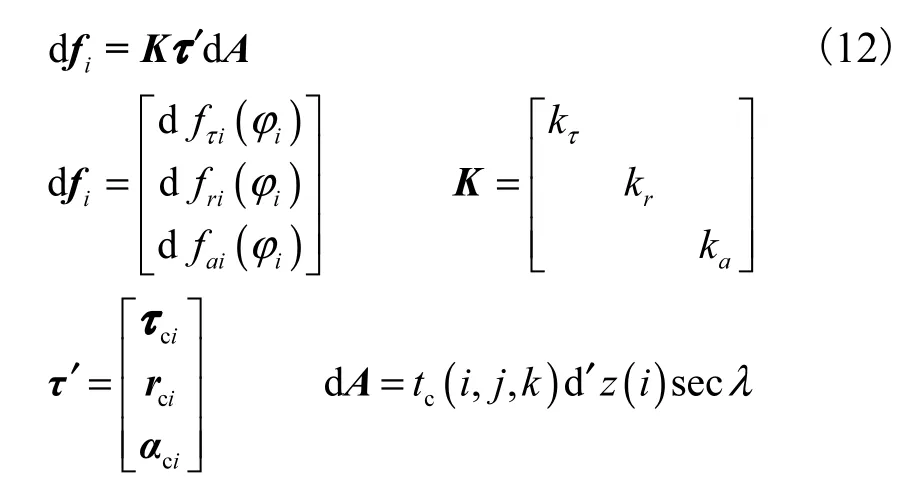
式中：kτ、kr、ka为与工件材料和切削参数有关的切削力系数，可通过参数识别方法[12]获得；τci、rci、aci为第i 个微单元的单位向量．

为了描述微单元上作用力的方向，在点oj建立如图2 所示的坐标系xjyjzj，则第i 个微单元的位置向量为

式中：φi为向量 ri的切削啮合角；e1、e2、e3分别为 xj、yj和 zj轴的单位向量；hi为第 i 个微单元距离铣刀底端的高度，hi=Rϕico tλ．

而铣刀刃上第 i 个微单元的单位向量可分别表示为

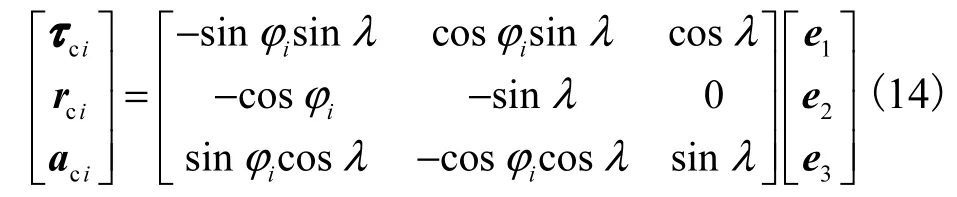
如果考虑铣刀前角γ对铣削力的影响，作用在铣削微单元上的铣削力可表示为

沿切削刃对微元铣削力式(15)积分，得到 t 时刻作用在整个刀刃上的铣削力为

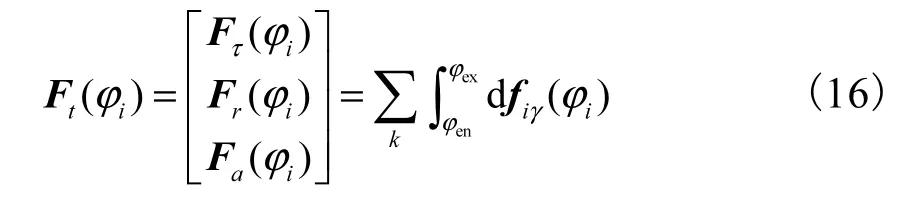
将作用在铣刀上的瞬时切削合力转化为x、y 和z方向上的分量 Fxj、Fyj、Fzj，可表示为

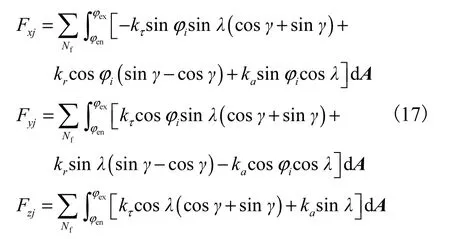
3 仿真分析

为了分析刀具和工件铣削形变对铣削力的影响，针对低刚度工件，采用小直径铣刀仿真高速切削过程中的弹性铣削形变和铣削力．在切削区域内，测试切削力用于刀具和工件形变预测，刀具形变预测的参数如表 1 所示，其形变预测曲线如图 4 所示．工件为薄壁立板，材料为铝合金 6082(弹性模量 E 为 69,GPa，泊松比μ为 0.33 ，布氏硬度 HB 为 100)，壁厚为2.5,mm．铣削方式为周铣，主轴转速为 24,000,r/min，每齿进给量为 0.04,mm/r，轴向铣削深度为 3.0,mm，径向铣削深度为 0.2,mm，采样频率为 1,500,Hz．经仿真其工件-刀具系统共同引起的法向综合形变曲线如图5 所示．

表1 立铣刀参数Tab.1 Specification of end mill cutter

如图4 所示，引起刀具形变的主要分力为法向分力 Frj和切向分力 Fτj．由于切向分力 Fτj在整个切削过程中基本不变，因此由该分力引起的刀具形变基本不变，其大小为 0.164,mm；而法向分力变化较大，由该分力引起的铣削形变较明显，其形变量由 0.294 mm 变化到0.335,mm．

图4 刀具铣削形变Fig.4 Variation of predicted deflection of cutter

预测形变反过来用于迭代计算，得预测铣削力，经仿真得到铣削力轮廓曲线如图 6 所示．由图 6 可知，法向铣削力随刀具的运动而变化，当刀具移动到工件长度的 1/2 时，法向铣削力达到最大，随后不断减小．

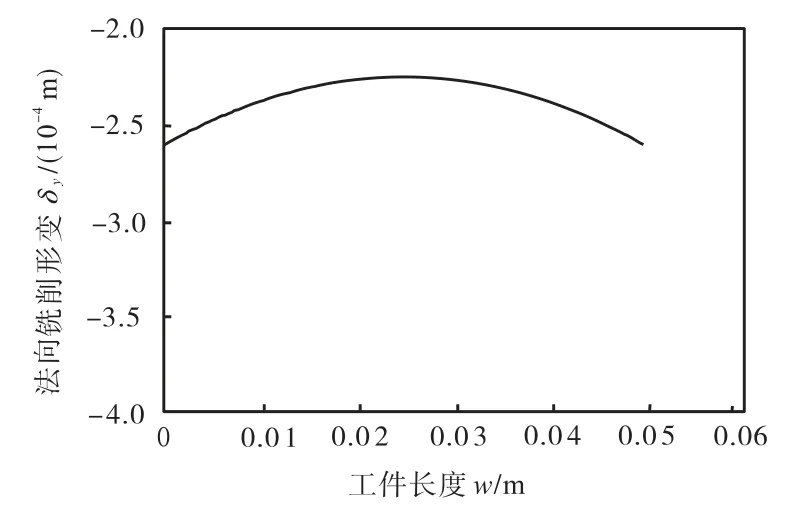
图5 工件-刀具法向铣削形变Fig.5 Workpiece-cutter deflection in normal direction

力的变化与形变的变化密切相关．由图 5 可知，工件-刀具的法向综合形变曲线为中间小两端大；从图6 所示的法向铣削力曲线可知，铣削力的变化曲线为中间大两端小．其主要原因是随着铣刀的切削运动，工件的刚度增大，弹性形变逐渐减小，“让刀量” 也逐渐减小，瞬时切削厚度随之增大，因此，铣削力逐渐增大．

图6 仿真铣削力Fig.6 Variation of predicted forces

4 试验验证

基于低刚度加工工艺系统的铣削力分析，采取一系列试验进行验证．试验装置如图 7 所示．试验在高速加工中心 DMG75V 进行，工件形状为3边自由1边夹紧的低刚度薄壁立板，铣削分力由 Kistler 动态测力仪测量．沿铣削长度方向测得法线方向上的铣削力 Frj以及切线方向上的铣削力 Fτj的曲线如图 8所示．在采样点上测得的法向、切向最大铣削力分别为 482 N、221 N，而仿真预测的法向、切向最大铣削力分别为 467 N、211 N．由测试和预测结果可知，铣削力的测量值和理论预测值具有较好的一致性．

图7 铣削形变试验装置Fig.7 Experimental setting-up of milling deflection

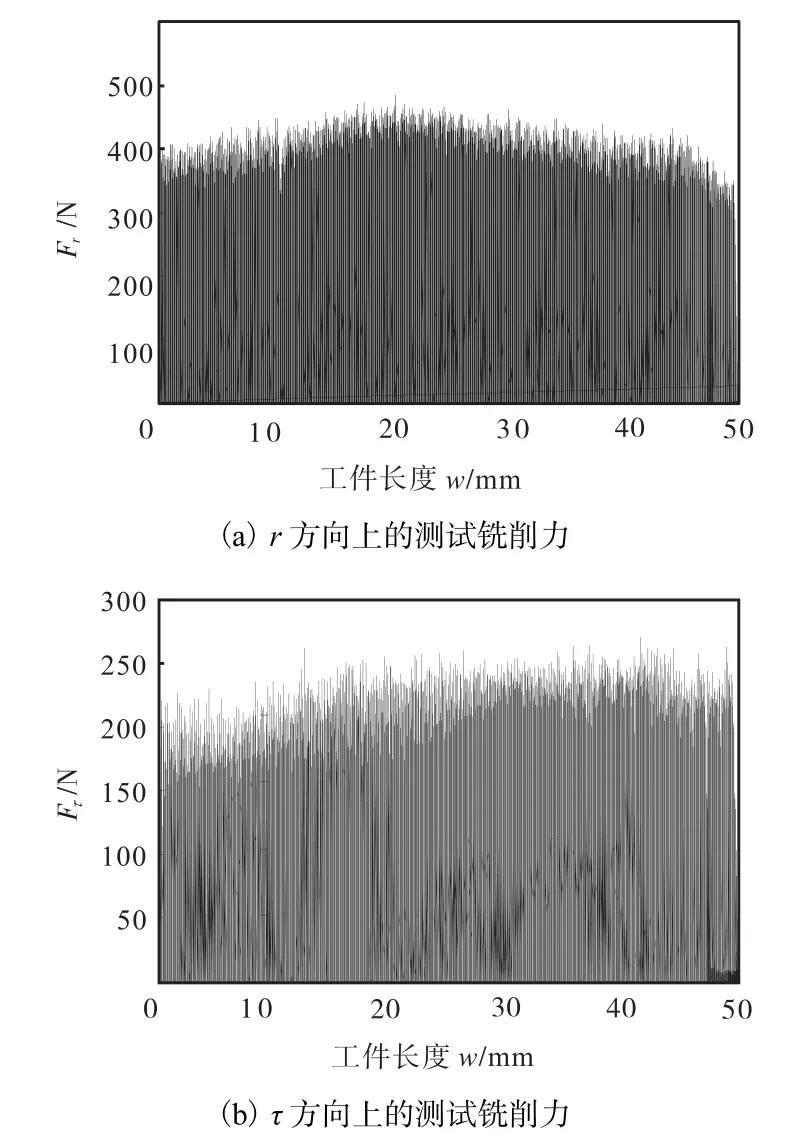
图8 测试铣削力Fig.8 Variation of measured forces

5 结 论

(1)基于低刚度薄壁工件-铣刀工艺系统，建立该高速铣削工艺系统的弹性铣削力模型．该模型考虑到工件和铣刀的弹性形变共同引起铣削啮合角的变化，并推导出啮合角的表达式；同时推导出了工件弹性铣削形变的解析式，计算出工件铣削啮合处的铣削形变，结合铣削力和工件-铣刀工艺系统弹性形变预测结果，通过迭代算法仿真出三向铣削力．

(2)经铣削试验验证，表明基于弹性铣削力模型仿真出的结果与实测数据具有较好的一致性．同时也表明了工件铣削形变与工件的刚度和铣削力密切相关，即工件铣削形变随铣削力的变化而变化；以及工件法向铣削分力是引起工艺系统形变的主要因素．

［1］Kim G M，Kim B H，Chu C N. Estimation of cutter deflection and form error in ball-end milling processes[J].Int J Mach Tools Manufacture，2003，43(9)：917-924.

［2］Shirase K，Altintas Y. Cutting force and dimensional surface error generation in peripheral milling with variable pitch helical end mills[J].Int J Mach Tools Manufacture，1996，36(5)：567-584.

［3］Salgado M A，de Lacalle L N L，Lamikiz A，et al.Evaluation of the stiffness chain on the deflection of endmills under cutting forces[J].Int J Mach Tools Manufacture，2005，45(6)：727-739.

［4］Xu Anping，Qu Yunxia，Zhang Dawei，et al. Simulation and experimental investigation of the end milling process considering the cutter flexibility[J].Int J Mach Tools Manufacture，2003，43(3)：283-292.

［5］Ong T S，Hinds B K. The application of tool deflection knowledge in process planning to meet geometric tolerances[J].Int J Mach Tools Manufacture，2003，43(7)：731-737.

［6］Ryu S H，Lee H S，Chu C N. The form error prediction in side wall machining considering tool deflection[J].Int J Mach Tools Manufacture，2003，43(14)：1405-1411.

［7］Ratchev S，Liu S，Huang W，et al. Milling error prediction and compensation in machining of low-rigidity parts[J].Int J Mach Tools Manufacture，2004，44(15)：1629-1641.

［8］Budak E，Altintas Y. Modeling and avoidance of static form errors in peripheral milling of plates[J].Int J Mach Tools Manufacture，1995，35(3)：459-467.

［9］Tsai J S，Liao C L. Finite-element modeling of static surface errors in the peripheral milling of thin-walled workpieces[J].Journal of Materials Processing Technology，1999，94(2)：235-246.

［10］万 敏，张卫红. 薄壁件周铣切削力建模与表面误差预测方法研究[J]. 航空学报，2005，26(5)：598-603.Wan Min，Zhang Weihong. Investigation on cutting force modeling and numerical prediction of surface errors in peripheral milling of thin-walled workpiece[J].Acta Aeronautica ET Astronautica Sinica，2005，26(5)：598-603(in Chinese).

［11］黄志刚，柯映林，王立涛，等. 基于正交切削模拟的零件铣削加工形变预测研究[J]. 机械工程学报，2004，40(11)：117-122.Huang Zhigang，Ke Yinglin，Wang Litao，et al. Study on prediction of the parts distortion due to milling machining based on orthogonal cutting simulation[J].Chinese Journal of Mechanical Engineering，2004 ，40(11)：117-122(in Chinese).

［12］Chiang S T，Tsai C M，Lee A C. Analysis of cutting forces in ball-end milling[J].Journal of Materials Processing Technology，1995，47(3/4)：231-249.