链传动啮合冲击理论分析及有限元模拟

许立新，杨玉虎，刘建平，张思献

(天津大学机械工程学院，天津 300072)

链轮轮齿滚子间啮合冲击载荷是引发链传动产生振动、噪声以及链轮、链节发生疲劳损坏的主要因素之一，因此，精确地分析与计算啮合冲击载荷是进行轮齿强度计算以及链传动系统动力学研究的重要内容之一．针对这一问题，国内外相关文献主要是围绕实验和有限元模拟开展研究．

Conwell 等[1-3]设计并建立了一套链传动实验系统，对轮齿滚子间的啮合冲击力及链条张力进行的测试，得出了一些有意义的结论．文献[4-5]通过建立链传动啮合冲击模型，分别对轮齿滚子间的啮合冲击作用进行了理论研究，并对冲击产生的噪声进行了实验测试．Zheng 等[6-8]在研究摩托车高速传动链振动和噪声时，首次采用有限元软件建立了链传动系统弹性动力学模型．文献[9]采用简化的单个滚子与轮齿啮合进行静应力分析研究，边界效应难以估算，必须做许多假设，计算结果只是一定程度上的近似．对链传动中啮合冲击特性进行有限元模拟，是含复杂接触条件的高度非线性动力学行为，精确确定高速运转链轮滚子啮合接触面的载荷以及接触点等边界条件是获得准确模拟结果的关键．

笔者以套筒滚子链为研究对象，结合理论分析和有限元模拟的方法，在相同参数条件下建立适用于实际应用的高速链传动系统有限元模型．通过有限元分析软件 ABAQUS 实现接触分析，采用动态显式分析方法，系统地模拟并研究具有标准齿廓形状的链轮滚子瞬时啮合冲击问题，以期为深入开展链传动系统动态特性研究提供一种更准确和有效的方法．

1 冲击应力理论计算

1.1 理论分析

链在传动过程中，冲击效应引起的齿面动载荷大小，取决于有效冲击质量、相对冲击速度、滚子轮齿间的接触刚度及接触阻尼．将冲击作用等效为在啮合瞬间具有等效质量m 的滚子以相对冲击速度 vrel在啮合点以一定的冲击角度与链轮轮齿发生冲击．如果取等效质量为1 个链节的质量，则产生的误差不超过5%[10]，因此，可以认为等效冲击质量为 1 个链节的质量．

相关文献对相对冲击速度进行了研究[11]，得出

式中：1r 为链轮半径；1ω为链轮角速度；z1为链轮齿数．

载荷作用下滚子与链轮相接触时，可视为平行圆柱体与凹型圆柱面在压力作用下的接触，如图 1 所示．为计算接触刚度k ，需先求得长方形接触区的宽度2b 及接触变形深度 h1、h2，根据赫兹应力公式得出

则接触刚度为

式中：P 为单位压力，N；l 为接触厚度；1μ、 2μ分别为滚子和链轮材料的泊松比；E1、E 2 分别为滚子和链轮材料的弹性模量；1ρ、2ρ分别为滚子和链轮齿沟圆弧的曲率半径．

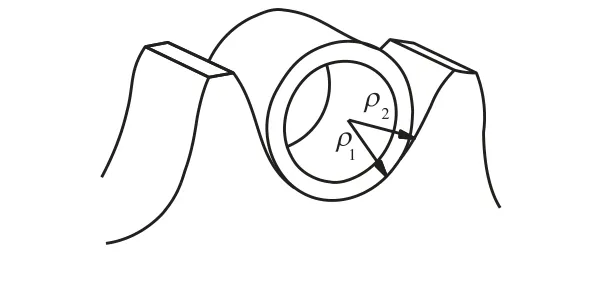
图1 链轮滚子啮合接触Fig.1 Meshing contact between sprocket tooth and roller

设滚子轮齿间的接触阻尼为黏性阻尼，在正常润滑条件下，取阻尼系数c 为0.1．

当滚子与轮齿接触时，其动力学方程为

链轮轮齿与滚子即将发生冲击接触时，方程满足初始条件[11]

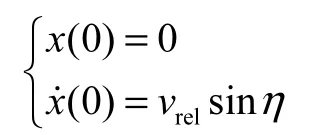
求解方程得

啮合频率为

当发生冲击作用时，满足条件 x (0) =0 ，代入式(7)得出

则在1 个滚子轮齿啮合周期内，冲击作用力为

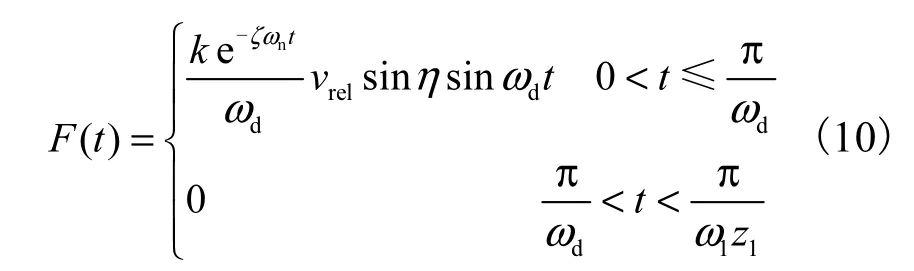
由赫兹应力公式得发生冲击作用时，最大接触应力为

1.2 算例分析

算例如下：通过1 组套筒滚子链传动系统参数建立链传动系统模型，为减小在仿真计算中有限元模型的规模，构建链传动系统结构参数如表 1 所示；选取链条参数如表 2 所示；主动链轮角速度1ω=62.8 rad/s；为使研究简便，选取链条各零部件材料为 45钢，材料特性如表 3 所示；以主动链轮轮齿受力为研究对象．

表1 系统主要参数Tab.1 Main parameters of system

表2 链条的主要尺寸参数Tab.2 Main size parameters of the chain

表3 材料特性Tab.3 Material properties

由链条参数计算等效冲击质量为

式中q 为每米链条的质量，q =1.02 kg/m．

相对冲击速度为

根据假设条件，同种材料相互接触时，μ1=μ2，E1= E2，则接触区宽度及接触深度为

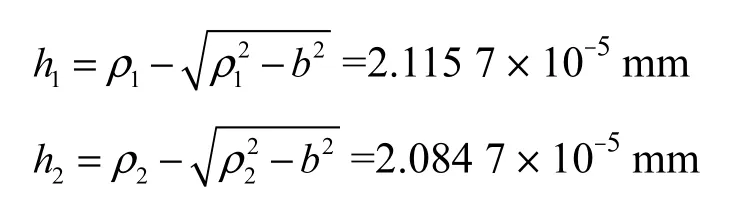
将结果代入式(5)，得接触刚度为

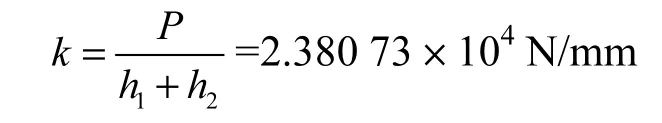
将等效质量、接触刚度及接触阻尼带入式(6)，求解动力学方程；通过式(10)，计算链轮滚子间啮合冲击接触力(简称冲击力)如图 2 所示，冲击力幅值Fmax=449.65 N．

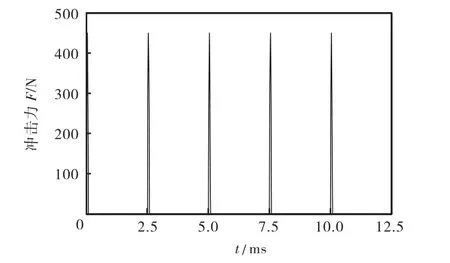
图2 轮齿滚子间冲击力Fig.2 Impact force between sprocket tooth and roller

将 Fmax代入式(11)，求得在冲击载荷作用下，接触应力为

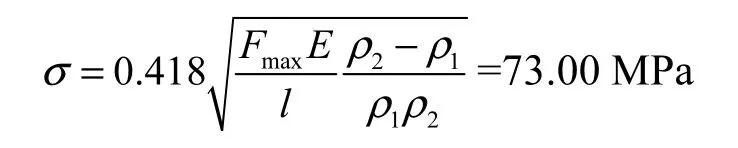
2 链传动系统有限元模型

2.1 仿真实体模型

根据国际标准及表1、表2 所示参数，在Pro/E 软件中编写套筒滚子链传动零部件结构设计程序，建立各零件实体模型．

链轮齿廓曲线相对比较复杂，其几何形状对应力分布有着明显的影响．为了精确模拟冲击过程中冲击接触力及应力的分布情况，采用三圆弧一直线齿型画法，精确建立链轮模型，如图 3 所示．图 4 为链节各零部件实体模型．

图3 链轮模型Fig.3 Model of sprocket

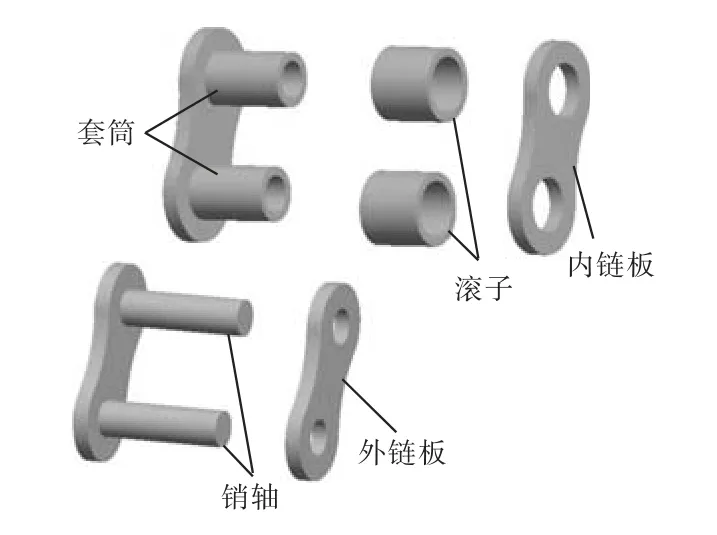
图4 链节零部件实体模型Fig.4 Solid models of chain components

2.2 有限元计算模型

把在 Pro/E 中生成的链传动系统模型文件读入ABAQUS 中，对链传动系统进行整体有限元计算，在系统动态仿真中研究链轮滚子间的啮合冲击动力学行为．对应表3，选取材料弹性模量为210 GPa，泊松比为0.3，材料密度为7 800 kg/m3．

对模型进行有限元网格划分．对于链系统这样比较复杂的模型，模型各部分的网格密度必须合理且合适才能既保证计算精度又节约计算时间．算例中采用重点区域(轮齿部分)细化网格的方法对链轮进行网格划分．单元选取 8 节点实体减缩积分单元(C3D8R)，采用该单元能够满足有限元显式计算要求，很好地保证计算精度，并能较好地逼近齿廓曲线边界．图 5 为套筒滚子链传动系统有限元模型，共146 954 个单元，最小单元尺寸0.4 mm．

在定义各零部件间的接触时，选用通用(自动)接触算法，该方法对于接触表面的类型限制较少，适合接触面多的复杂模型，取接触摩擦系数为0.1．

图5 套筒滚子链传动系统有限元模型Fig.5 Finite element model of the roller chain drive system

2.3 定义边界条件

图6所示为链传动系统有限元模型速度边界条件的定义．为了保证模型计算中的平稳性，主动链轮的角速度以 STEP 函数的形式加载，在 1,ms 的时间历程中，速度由零逐渐达到规定值．

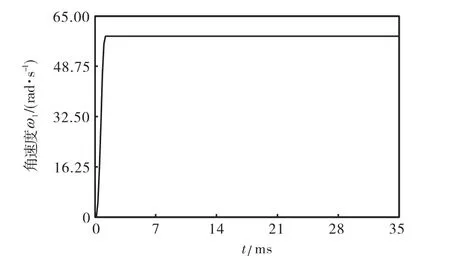
图6 速度边界条件Fig.6 Velocity boundary condition

在链传动有限元计算中，模型比较庞大，所需空间和内存非常大．计算在 DELL8CPU、32G 内存的工作站上进行．

3 结果与讨论

为对结果进行详细的分析和讨论，以连续的5 次冲击作用为统计对象，研究轮齿滚子瞬时啮合时的齿间载荷变化规律和接触应力分布情况．

3.1 冲击力变化规律

图7所示为主动链轮在连续 5 次啮合冲击作用下，冲击接触力的变化情况；表 4 给出了每次冲击作用中冲击力峰值及平均值．

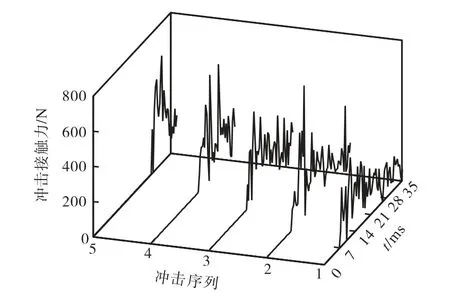
图7 冲击接触力Fig.7 Contact impact force

表4 冲击接触力的峰值及平均值Tab.4 Maximum and mean values of contact impact force

冲击作用发生后，轮齿滚子间的接触力达到最大值，并随着时间逐渐减小．冲击力平均幅值为 585.00 N，高出理论计算值449.65 N 近30%．

3.2 轮齿冲击应力变化规律

图8所示为某次冲击作用下，链轮轮齿冲击动应力分布云图．图 9 为在连续 5 次啮合冲击作用下，冲击接触动应力变化情况．表 5 给出了轮齿齿面冲击动应力峰值及平均值，冲击动应力平均值为 91.85 MPa．

图8 轮齿冲击动应力云图Fig.8 Stress nephogram on sprocket tooth caused by impact

图9 轮齿冲击动应力Fig.9 Dynamic stress on sprocket tooth caused by impact

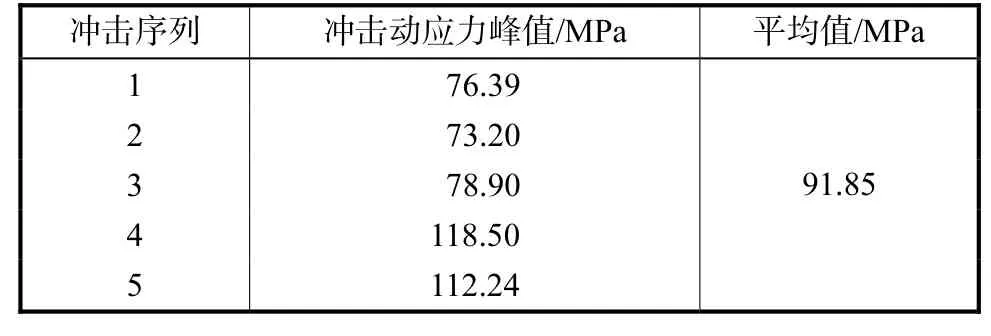
表5 轮齿冲击动应力的峰值及平均值Tab.5 Maximum and mean values of dynamic stress on sprocket tooth caused by impact

3.3 滚子冲击应力变化规律

图10所示为某次冲击作用下，滚子冲击动应力分布云图．图 11 为在连续 5 次啮合冲击作用下，其冲击接触动应力变化情况．

表6 给出了滚子冲击动应力峰值及平均值，冲击动应力平均值为83.81,MPa．

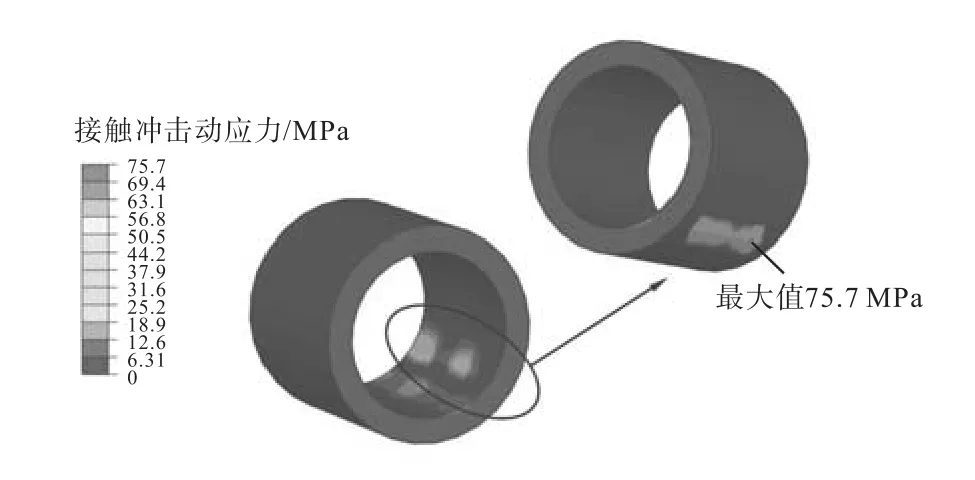
图10 滚子冲击动应力云图Fig.10 Stress nephogram on roller caused by impact

图11 滚子冲击动应力Fig.11 Dynamic stress on roller caused by impact

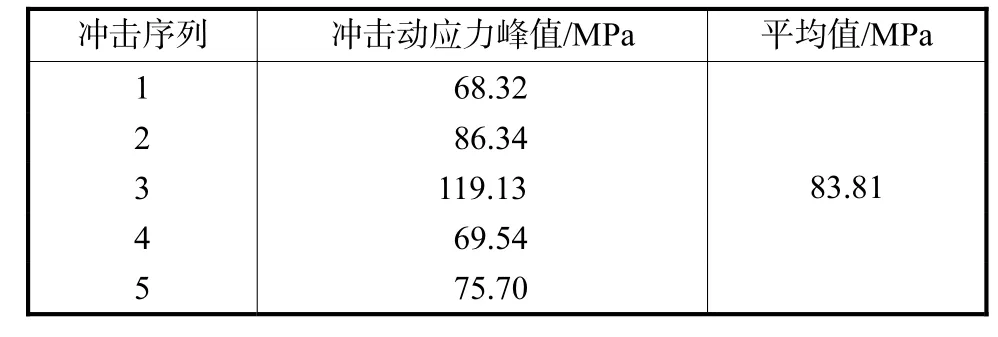
表6 滚子冲击动应力峰值及平均值Tab.6 Maximum and mean values of dynamic stress on roller caused by impact

通过比较有限元模拟结果与理论计算结果发现，轮齿齿面及滚子柱面所受冲击动应力高出理论计算值73.00,MPa 近15%～25%，表明动态冲击载荷远大于静态条件下的理论计算值．另外，采用赫兹接触理论，在接触动应力的理论计算中，认为发生接触的区域为长l 、宽2b 的长方形区域；而有限元模拟结果表明，接触区域变形并非理想的长方形区域，轮齿齿面和滚子间的冲击接触力分布是不均匀的，接触动应力存在突变．

4 结 论

(1)基于三维弹性接触有限元分析方法，建立了套筒滚子链传动系统有限元模型．该模型考虑了系统各零部件标准几何实体形状、摩擦及间隙等多种复杂影响因素，能够较精确地揭示该类系统的冲击特性．这为深入开展链传动系统的动态特性分析提供了一个可行的方法．

(2)利用 ABAQUS 软件对轮齿滚子间的啮合冲击效应进行了数值模拟，较为精确地得出了轮齿冲击力、动应力大小及其分布规律，为开展链轮轮齿强度分析提供了借鉴．

(3)在系统动态条件下，有限元模拟结果表明，轮齿滚子作为弹性体发生冲击接触时，接触区域变形并非理想的长方形区域，轮齿齿面的冲击接触力分布是不均匀的，在理论接触区域两侧冲击动应力较大．这为研究消除轮齿齿面载荷突变及应力集中现象提供了借鉴．

(4)比较有限元模型模拟与理论计算结果发现：啮合冲击力幅值比理论计算结果高 30%；冲击动应力幅值比理论计算结果高 15%～25%．说明在考虑了链轮齿形、间隙及弹性变形等多种影响因素的条件下，动态冲击载荷远大于静态条件下的理论计算值．

［1］Conwell J C，Johnson G E，Peterson S W. Experimental investigation of the impact force that occurs when a roller seats on the sprocket during normal operation of a roller chain drive [C]//Proceedings of the 1992 International Power Transmission and Gearing Conference. Scottsdale，AZ，USA，1992，43：717-721.

［2］Conwell J C，Johnson G E. Experimental investigation of link tension and roller-sprocket impact in roller chain drives [J]. Mechanism and Machine Theory ，1996 ，31(4)：533-544.

［3］Conwell J C，Johnson G E. Design，construction and instrumentation of a machine to measure tension and impact forces in roller chain drives [J]. Mechanism and Machine Theory，1996，31(4)：525-531.

［4］Wang K M，Liu S P，Havek S I，et al. On the impact intensity of vibrating axially moving roller chains [J].Journal of Vibration and Acoustics，1992，114(3)：397-403.

［5］Liu S P，Wang K W，Havek S I，et al. A global-local integrated study of roller chain meshing dynamics [J]. Journal of Sound and Vibration，1997，203(1)：41-46.

［6］Zheng H，Wang Y Y，Liu R，et al. Efficient modeling and prediction of meshing noise from chain drives [J]. Journal of Sound and Vibration，2001，245(1)：133-150.

［7］Zheng H，Wang Y Y，Quek K P，et al. Investigation of meshing noise of roller chain drives for motorcycles [J].Noise Control Engineering Journal，2002，50(1)：5-11.

［8］Zheng H，Wang Y Y，Quek K P，et al. A refined numerical simulation on dynamic behavior of roller chain drives[J]. Shock and Vibration，2004，11(5/6)：573-584.

［9］刘海蓉，芮执元，鲁春朋. 冷却运输机滚子输送链的接触分析研究[J]. 计算机与数字工程，2007，35(3)：38-39，70.Liu Hairong，Rui Zhiyuan，Lu Chunpeng. The contact analysis and study of conveyor bush-roller chain in cooling transporter[J]. Computer and Digital Engineering，2007，35(3)：38-39，70(in Chinese).

［10］Chew M. Inertia effects of a roller-chain on impact intensity[J]. Journal of Mechanisms，Transmissions，and Automation in Design，1985，107(1)：123-130.

［11］Choi W，Joinson G E. Vibration of roller chain drives at low，medium and high operating speeds [C]// Proceedings of the 14th Biennial ASME Conference on Vibration and Noise. Albuquerque，NM，USA，1993，63：29-40.