表面活性剂水溶液的电导率研究方法和一些特征数据的提取

赵剑曦

(福州大学化学化工学院,胶体与界面化学研究所,福州 350108)

表面活性剂水溶液的电导率研究方法和一些特征数据的提取

赵剑曦

(福州大学化学化工学院,胶体与界面化学研究所,福州 350108)

电导率是研究水溶液中离子型表面活性剂胶束化行为的重要方法,本文总结了这个灵敏测定技术,分别着重讨论了两个重要特征参数(临界胶束浓度(cmc)和胶束的反离子解离度(α))的提取方法、电导率曲线某些特殊情况的分析以及预胶束化行为的研究,这对运用电导率技术研究当前不断增多的具有强分子间相互作用的表面活性剂(例如Geminis)体系具有参考价值.

离子型表面活性剂;电导率;特征数据

离子表面活性剂在水溶液中能电离成活性离子和反离子,因而在电场下呈现出定向运动,这即电导率(κ,specific conductivity)测定的依据.电导率测定是一种灵敏的测量方法,在表面活性剂溶液的各种研究方法中占有重要地位[1].例如,当离子型表面活性剂自组织生成胶束时,水溶液中的导电粒子除了反离子外,大部分的单个表面活性剂离子转变为多分子聚集的胶束,由于胶束粒子远大于单个表面活性剂离子,因此可由电导率法精确且方便地测定这一变化过程.如果将测定信号转变为摩尔电导率,可以间接反映正常胶束生成之前溶液中可能出现的预胶束化现象[2].微分电导率甚至更可直接获得预聚集的信息[3].在高表面活性的Gemini表面活性剂问世后,由于超强的分子间相互作用,Gemini表面活性剂的临界胶束浓度(cmc)通常很小,溶液中的聚集行为和生成的聚集体结构也远比传统表面活性剂复杂,灵敏的电导率测定方法显示了优越性,但特征数据的提取和对复杂电导现象的理解成为运用这一技术的关键,本文就这个问题进行讨论.

1 临界胶束浓度及其数据提取

当表面活性剂浓度超过某一临界值时,烷烃链因疏水相互作用而自发聚集成胶束,这一特征浓度称为临界胶束浓度(cmc).胶束是多个表面活性离子构成的核-壳结构聚集体,由于头基电荷的相对集中,胶束表面束缚住部分反离子,这种表观的束缚现象被表征为胶束的反离子结合度K0(或反离子解离度α,α=1-K0).胶束尺寸增大和束缚部分反离子,致使其在电场下的运动受到一定程度的阻碍,电导率曲线(κ-C)在cmc处呈现了转折,依据这一特征可由转折点获得cmc.cmc是研究表面活性剂胶束化的重要参数,不仅反映了聚集的能力,还可以由cmc获得胶束化过程的热力学参数以及了解混合胶束的组成.热力学参数包括胶束化过程的Gibbs自由能变化ΔGmic,焓和熵的改变ΔHmic和ΔSmic.其中ΔGmic通过cmc并结合胶束反离子结合度K0获得[4],Zana给出了Gemini表面活性剂计算ΔGmic公式[5]

ΔG0mic=RT(1+2K0)ln cmc+2RTK0ln2 (1) ΔHmic和ΔSmic则由不同温度的cmc值间接获得[6].相比较而言,微量热法可直接测得ΔHmic[7-8],但仍旧需要由式(1)计算,因此电导率法显得简单方便.混合胶束组成迄今尚没有其它技术可以直接测定,在获得cmc后由Rubingh-Rosen规则溶液理论进行估计[9-11].上述这些方法均依赖cmc数据来获得结果,可见准确的cmc值至关重要.

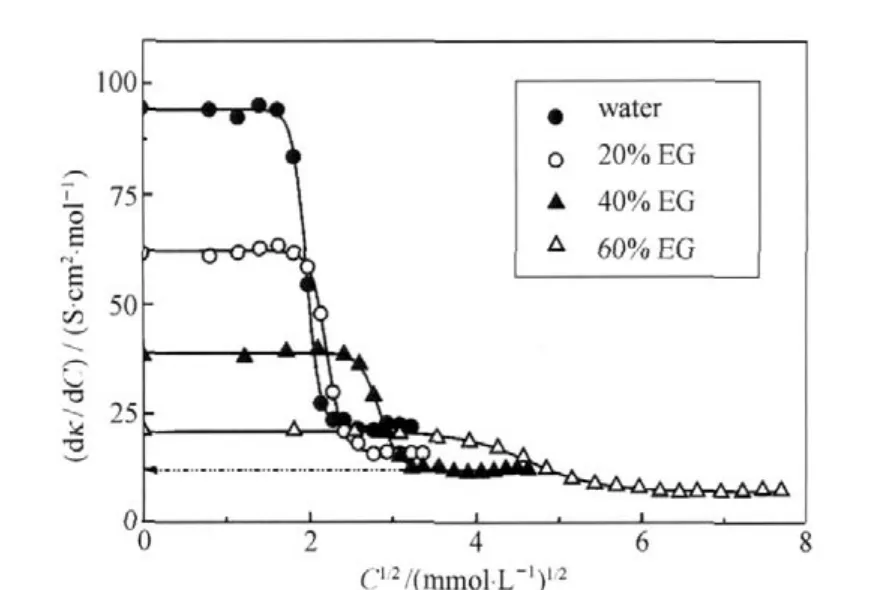
图1 C14TABr/乙二醇(EG)混合水溶液的微分电导率曲线[16]Fig.1 Plots of differential conductivity for mixed C14TABr/ethylene glycol aqueous solutions[16] The cmc can be determined by the turning point of the curve going down.

人们为此进行了很多的努力,例如Manabe[12]、Sugihara[13-15]和Ruiz[16]等利用微分电导率(即κ对C的一阶导数,dκ/dC)随C1/2变化曲线在胶束开始生成时呈现出更为清晰转变的特点来确定cmc(一个典型例子见图1,关于微分电导率应用的进一步讨论见第5、6节).又如Carcía-Mateos和Zhao 等用数据的二阶导数(d2κ/dC2)曲线的极大值点来确定cmc.这两种方法对诸如十二烷基硫酸钠(SDS)或十二烷基三甲基溴化铵(C12TABr)、十四烷基三甲基溴化铵(C14TABr)等在κ-C曲线出现明显转折点的例子中确实比目视法更可靠,避免了人为的误差 (图2),但对Gemini那样具有分子间强相互作用的例子则并不完全可行,这样的电导率曲线在cmc时出现了缓慢的过渡,而不是清晰的转折点.我们先前曾利用Zhao等[18]推荐的Lorentzian方程(d2y/dx2=-k1/[k22+ (x-x0)2])拟合季铵盐Gemini表面活性剂体系以及它与C12TABr混合体系的实验数据,结果发现有些体系由于电导率曲线的转折过渡区较大,二阶导数极值点仅仅对应了电导率开始过渡变化的初始区间,不能很好地给出cmc.

在更早期,Phillips[20]定义了cmc是表面活性剂溶液的某一性质(φ)与浓度关系曲线的变化梯度出现最大变化所对应的浓度,此时有(d3φ/dC3)C=cmc=0. Williams等[21]则考虑cmc作为胶束浓度为0的点,之后胶束浓度开始增加.在这两个定义的基础上, Pérez-Rodríguez等[19]利用二阶导数法,引进Runge-Kutta数字积分和Levenberg-Marquardt最小二乘方拟合算法,发展了确定cmc的新方法.但他们引用的处理例子主要还是局限在SDS和C12TABr等简单的情况,出现两个转折点的盐酸氯丙嗪例子见图3.

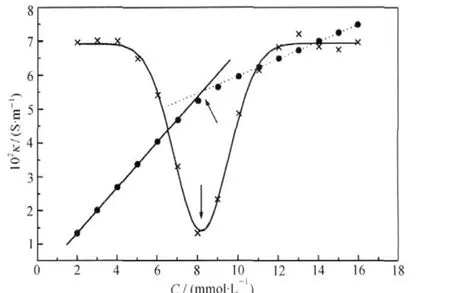
图2 25℃时SDS的电导率曲线(●)以及二阶导数曲线(×)[19]Fig.2 Specific conductivity(●)of SDS in water as a function of molar concentration at 25℃and the corresponding second derivative curve(×)[19] The cmc can be determined by the minimum of second derivative curve.

图3 25℃时盐酸氯丙嗪的电导率曲线(实线)以及按Pérez-Rodríguez假设方法计算的二阶导数曲线(虚线)[19]Fig.3 Specific conductivity of chlorpromazine hydrochloride in water as a function of molar concentration at 25℃(solid line)and the corresponding second derivative curve(dotted line)[19] The two minima correspond to the two cmcs.

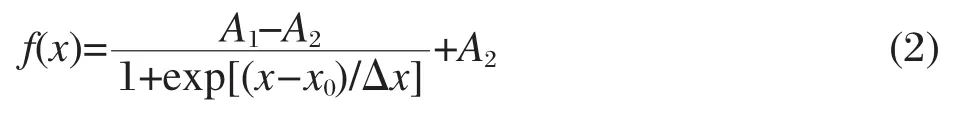
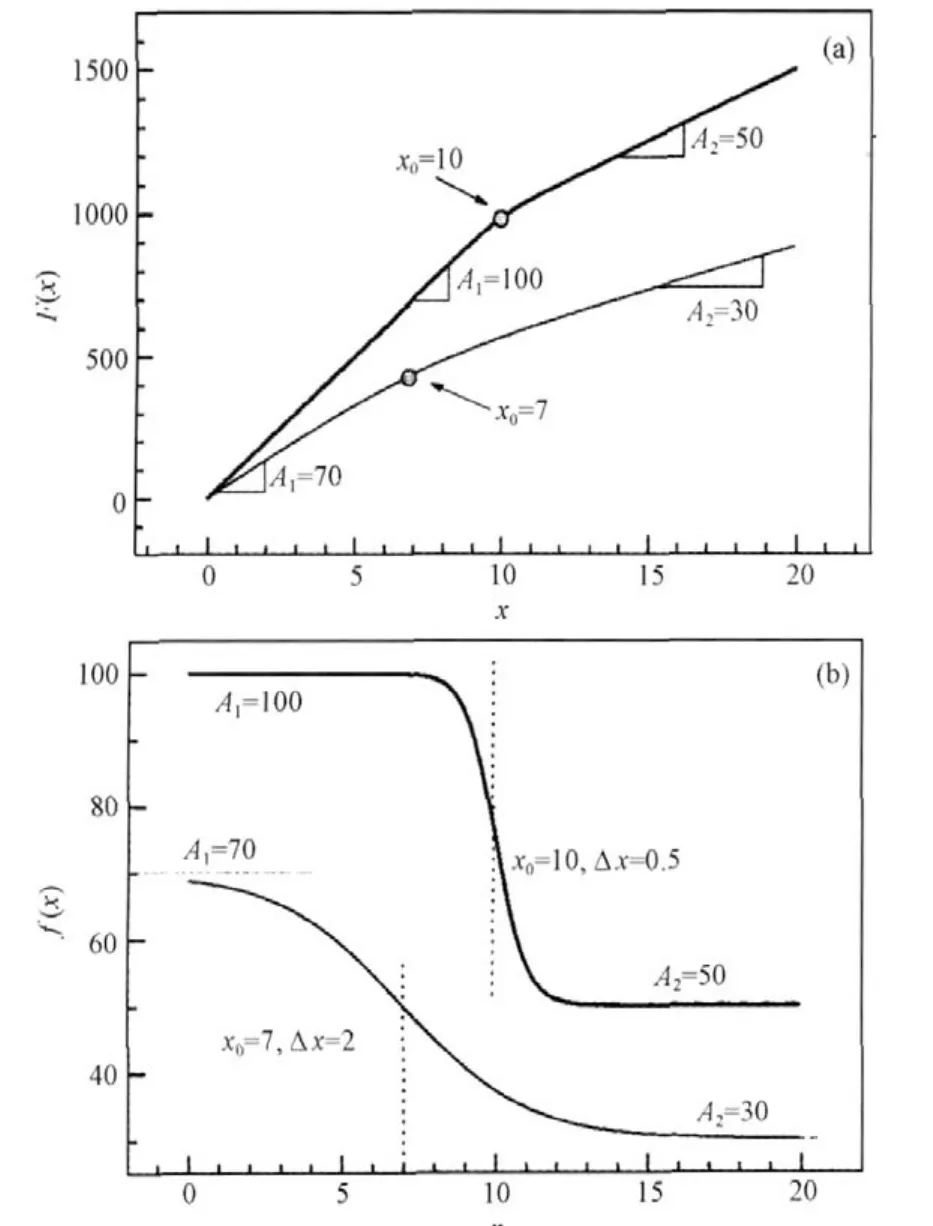
图4 两种不同转折宽度的F(x)和f(x)的理论计算曲线[22]Fig.4 F(x)and f(x)curves calculated theoretically for two different transition widths[22]

近来,Carpena等[22]发展了更合适确定cmc的方法,他们详细分析了电导率曲线和它的一阶导数的特征,提出以Boltzmann形式的方程(式(2))来描述电导率的一阶导数f(x):式中A1和A2分别为小x和大x范围曲线的渐近值(见图4b),x0为电导率数据出现转变所对应的中心点(the central point of the transition),Δx表达了转变的宽度.一阶导数所反映的电导率原始数据则作为上式的积分F(x):

图4给出理论计算的f(x)和F(x),可以看到越大的宽度Δx意味着电导率曲线在交点处变化越缓慢.他们进一步应用基于Levenberg-Marquardt最小二乘方拟合算法的非线性拟合法与Monte Carlo模拟的结合方法,验证了这个方法的适用性.结果证实该方法不仅对SDS或C12TABr,而且对C16TABr(出现了cmc的缓慢过渡)也能给出准确的cmc值(图5).不仅如此,拟合获得的常数A2和A1的比值A2/A1可以很好地表征胶束的反离子解离度α,能与通常依据cmc之上和之下两条直线斜率比值(S2/S1)方法[23]获得的数值相吻合.Quagliotto等[24]在之后研究新型的葡萄糖基阳离子表面活性剂的电导率行为时,特别指出Carpena推荐的Boltzmann形式方程尤其适用于处理在cmc范围内电导率缓慢过渡的例子,能够很好地确定临界胶束浓度.我们在研究季铵Gemini同系混合物胶束化行为应用这个方法获得了很好的效果[25].Quagliotto等[26]最近以这个数学方法处理芘探针的I1/I3曲线,确定了季铵盐Gemini表面活性剂16-3-16和16-4-16的cmc,其值与该方法应用于电导率曲线获得的cmc一致.

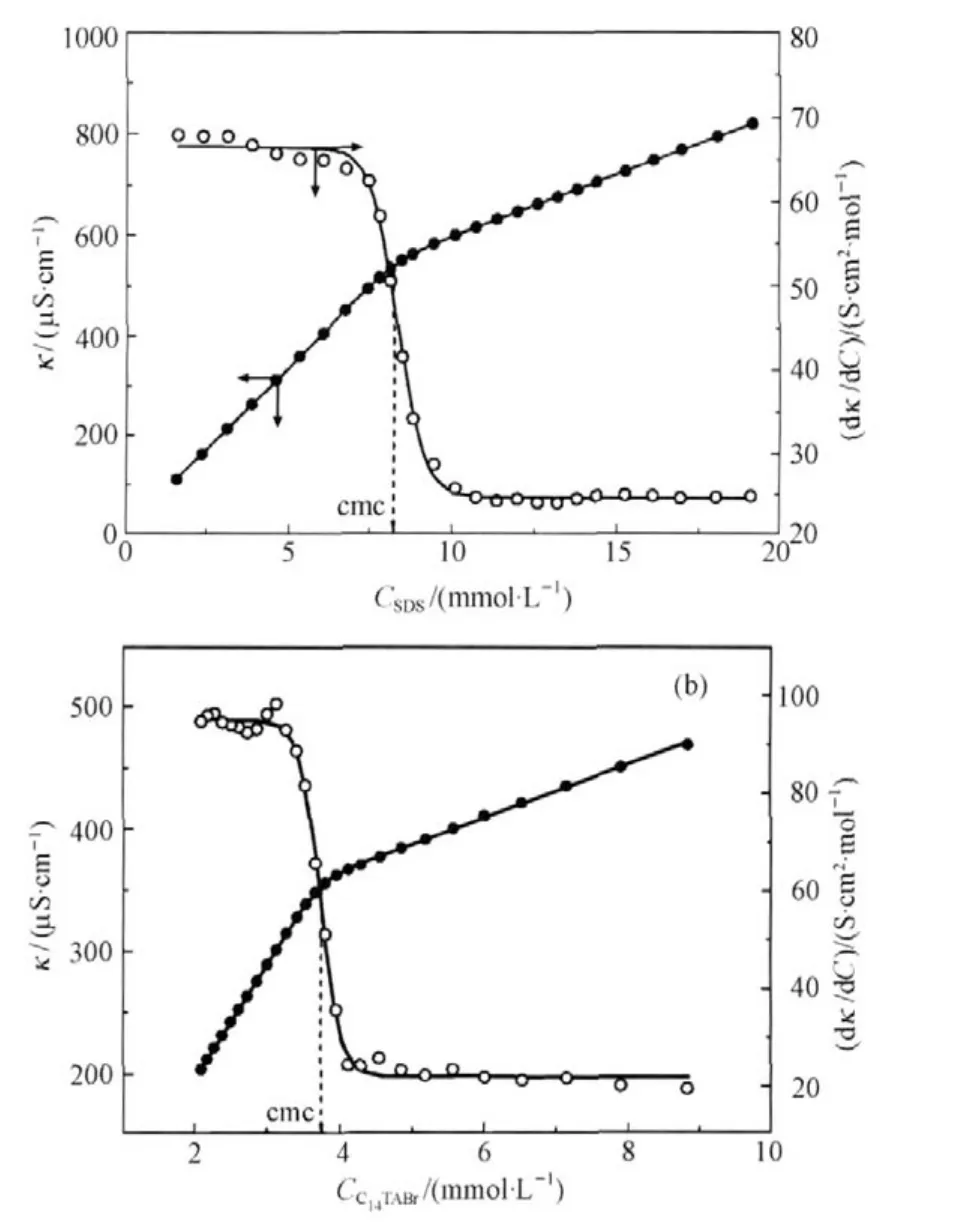
图5 25℃时SDS(a)和C14TABr(b)的电导率实验数据以及计算的F(x)和f(x)曲线[22]Fig.5 Experimental data of conductivity vs concentration,F(x),and their corresponding first derivative,f(x),for SDS(a)and C14TABr(b)at 25℃[22]

2 电导率法测定第二cmc

将κ-C曲线延伸到浓度较大的范围,有时会观察到两个转折点,分别对应第一cmc和第二cmc,如图3给出的例子.第二cmc的出现意味着溶液中的聚集行为发生了变化,其意义应根据不同体系判断.例如十六烷基苄基二甲基氯化铵(C16BzCl)/十六烷基氯化吡啶(C16PyCl)混合水溶液体系,观察到在C约为3cmc时的第二个转折点(图6),这被解释为聚集体结构发生了转变[27].尽管电导方法本身并不能直接获得聚集体结构的信息,但由于方法的高敏感性和便利性,可以提示溶液中聚集体形态的变化.又如,季铵盐Gemini表面活性剂12-3-12和Brij35混合水溶液体系也存在第二cmc,认为第一cmc对应纯Brij35胶束,而第二cmc时形成了混合胶束[28].

3 胶束表面反离子解离度的电导率方法测定

如上节讨论可知,电导率曲线κ-C在cmc以下和以上表现为两条斜率分别为S1和S2的直线,很多文献(例如近期的Hirata等[23])建议可由这二个斜率比S2/S1来简单表征α值.在cmc以下经过原点的直线相对较易确定,其斜率S1也因此容易获得,但是cmc以上的直线就要特别注意,需要尽可能向较高浓度延伸,以保证直线斜率的准确,这样才能获得正确的α值.

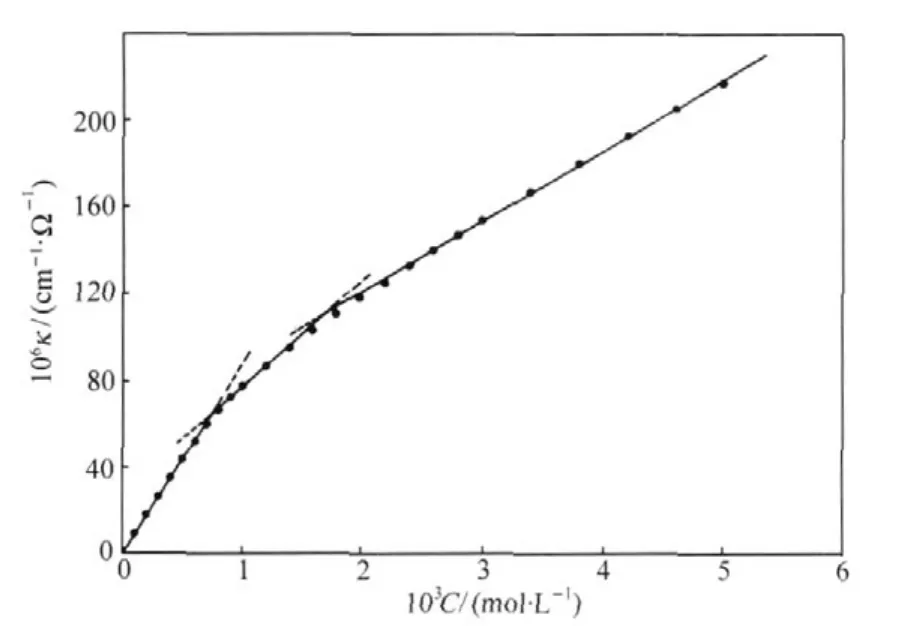
图6 十六烷基苄基二甲基氯化铵(C16BzCl)/十六烷基氯化吡啶(C16PyCl)混合水溶液(xC16BzCl=0.20)的电导率曲线[27]Fig.6 Conductivity plot of hexadecylbenzyldimethylammonium chloride (C16BzCl)and hexadecylpyridinium chloride(C16PyCl) mixed aqueous solution at xC16BzCl=0.20[27]

Evans[29]提出了另一种确定α的方法,该方法结合单头基单烷烃链表面活性剂胶束几何模型建立了计算α的公式:

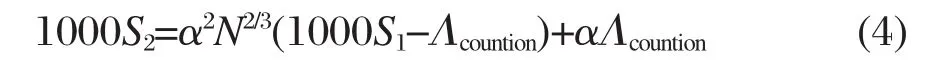
式中N为胶束的聚集数,Λcountion为反离子的摩尔电导率(S·cm2·mol-1),并且用到了电导率曲线的斜率S1和S2,这样的处理其物理意义更加明确.

Gemini的分子结构不同于普通表面活性剂,我们[30]进一步提出了如下计算公式:

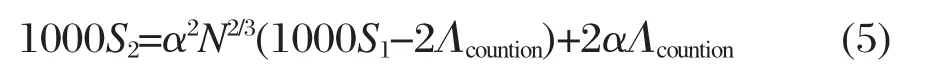
上述公式已成功地用于季铵盐Gemini表面活性剂胶束反离子解离度α的计算[30].

有了胶束反离子解离度α,反离子的结合度K0很容易得到:

除了电导率方法外,采用离子选择性电极直接测定反离子也能获得α或K0[31-32].早期也有利用测定不同盐溶液中cmc,再根据以下线性公式由斜率求出K0[33]:

式中n为表面活性剂离子头基的个数,Ci为反离子浓度.在这个方法中,K0值与无机盐的性质有关[34].相比较而言,电导率方法较为简便,可同时获得cmc和K0.

4 电导率曲线的某些特殊情况

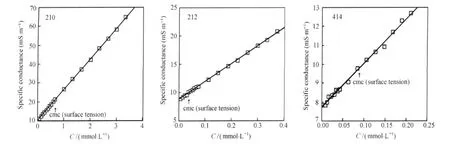
图7 双氨基丙酸钠Gemini表面活性剂的电导率曲线[36]Fig.7 Specific conductance vs molar concentration plots for the alkanediyl-α,ω-bis(sodium N-acyl-β-alaninates)Gemini surfactants[36]210 represents the lengths of the acyl chain n+1=10 and of the polymethylene spacer m=2,212 is n+1=12 and m=2,and 414 is n+1=14,m=4.

电导率曲线(κ-C)是由两条相交于cmc的不同斜率的直线构成,其中低浓度区间的直线理应过原点(如果表面活性剂浓度很稀,溶液电导率很小,需要扣除水的微量电导率才可以使直线过原点).但低浓度区间的实验测试点在两种情况下可能会偏离直线.(1)溶液中活性离子与反离子形成了离子对(ion pairing).我们知道表面活性物质在很稀浓度通常完全电离为相反电性的组分,随着浓度增加,这些相反电性的组分可能结合形成离子对,离子对中和了电性,致使溶液电导率下降.浓度越高,离子对现象越显著,电导率值下降也越明显,于是表现为在接近cmc时的测定数据点偏向坐标横轴(浓度轴)[35].Zana[35]建议这样的偏离可以用来表征离子对的形成,偏离得越明显,表明溶液中离子对形成越多.(2)溶液中出现了预胶束化行为.所谓的预胶束是指在cmc(正常胶束形成时的临界浓度)之前活性离子在溶液中就已经形成了某种结构不完整的小聚集体(可能是二聚体、三聚体等低聚体),这对于那些具有强烈相互作用的表面活性剂体系显然是可能的.预胶束行为的存在说明表面活性剂的聚集事实上并不是完全的突变现象,对那些相互作用不那么强烈的两亲分子来说,它们必须在气/液界面吸附饱和后再发生溶液中的聚集,于是在用表面张力测定时似乎感觉到这样的聚集是突变行为,但是对那些具有强烈相互作用的两亲分子,吸附和聚集可能同时进行,这就使得在气/液界面吸附尚未达到饱和时,溶液中就有了部分的预聚集.我们的工作发现某些具有强烈分子间相互作用的体系(例如Gemini与相反电性的表面活性剂混合体系),强烈的预胶束化行为甚至可以使表面张力几乎不变,但直接测定溶液体相内粒子变化的技术(例如电导率或荧光探针)已经出现了明显改变的信号.由于预胶束是少数几个完全解离的表面活性离子构成的小聚集体,因而促进了溶液电导,使之在接近cmc时的实验测试点偏向坐标纵轴(κ轴)[35].从上述讨论可见,这两方面偏离直线的原因都发生在cmc附近,因此确定cmc以上那条直线的走向(即斜率)变得较为困难,如果仅测定少数几个点(既延伸的浓度不够大),可能造成直线确定的错误,我们根据实践建议需要测定到3倍cmc以上浓度,以保证直线斜率的相对准确.

有时,电导率曲线在cmc区间并没有出现明显的转变,一直保持着原先在低浓度区的直线斜率继续上升.例如Tsubone等[36]在测定双氨基丙酸钠Gemini表面活性剂电导率曲线时,发现在表面张力测定的cmc周围,电导率直线一直上升,没有出现变化的迹象(图7).已知在cmc之前的低浓度区间,电导率随浓度增加而线性增大的原因来自这时候表面活性剂完全解离.由于反离子尺寸远小于表面活性离子,因而此时的电导率主要反映了解离出的反离子的导电行为.既然如此,在cmc(表面张力法测定)之后,电导率依旧照此斜率继续上升,表明增加的反离子数量仍旧按照完全解离的方式进行,就是说形成的胶束其表面几乎不结合反离子.这种现象虽然少见,但给我们提供了推断胶束微观结构的一个实验证据.

5 预胶束化行为的电导率方法判定

表面活性剂的预胶束化是常见的行为[37-41],尤其对分子间强相互作用的Gemini体系[2,35-36,42-51].由于常规测试技术难以表征很小的预胶束,通常都只能得到间接的信息,例如表面张力曲线出现了双转折点[52],cmc与烷烃链长度m的半对数关系偏离了直线[36,44,48],摩尔电导率Λ-C1/2曲线的极大值行为[2,35],荧光探针[45-46]或NMR[50]技术等.与反映界面行为的表面张力技术比较,直接表征溶液中粒子行为的电导率法、荧光探针或NMR技术更为可靠.但对于很小的预胶束来说,外加的荧光探针分子可能造成干扰.与NMR法相比,电导率法显得简便.

Zana[2,35]建议以摩尔电导率Λ-C1/2曲线的极大值来判定溶液中的预胶束行为.单分散状态的表面活性剂处于完全电离状态,Λ随着浓度增加而增大;当出现聚集后,由于聚集体尺寸明显增大,运动速度远低于单体离子,于是Λ开始下降.在没有预胶束化的情况下,Λ-C1/2曲线的极大点恰好对应了cmc.如果极大点出现在cmc之前,则预示着预聚集体的存在.在先前的文献中,Pinazo等[47]已结合模型给出了定量的解释.摩尔电导率Λ=(κ-κ0)/C,式中κ0为水的电导率,可见由测定的电导率κ很容易转化为Λ.图8给出25℃时联接链为不同数量亚甲基的季铵盐Gemini表面活性剂10-3-10、14-8-14,联接链为对苯二甲基(p-xylylene)的季铵盐Gemini表面活性剂16-xylyl-16以及C12TABr的κ-C和Λ-C1/2曲线,可见更疏水的14-8-14和16-xylyl-16体系其ΛC1/2曲线出现了极大点,意味着发生了预胶束行为.

在预胶束存在下,根据电导率曲线Λ-C转折点得到的cmc往往会比表面张力法得到的偏大很多,例如Quagliotto等[24]在考察新型的糖基化阳离子表面活性剂时,发现电导率法得到的cmc是表面张力法得到的2-8倍,这被认为与溶液中预胶束的存在有关.由于cmc代表溶液中形成正常胶束的临界浓度,表面张力曲线在转折点时仅仅表示气/液界面达到了饱和吸附,在没有预胶束行为时,其转折点很好对应了cmc,与电导率方法测定结果一致.当存在预胶束行为时,达到饱和吸附有时并不意味着溶液开始生成正常胶束,因此在预胶束化情况下电导率方法获得的cmc才真正对应了正常胶束形成的临界浓度.

微分电导率以dκ/dC表示,即在κ-C曲线任一浓度时的曲线斜率,由最相邻的两个浓度C1和C2通过式(κ2-κ1)/(C2-C1)计算得到.当作dκ/dC-C或C1/2图时,对应的浓度通常取平均值,即(C1+C2)/2. Mukerjee和Yang[53]是最早利用微分电导率研究表面活性剂溶液性质的两位先驱者.其后,Carcía-Mateos等[17]采用二阶微分电导率d2κ/dC2来确定离子表面活性剂的cmc.更系统的工作则由Manabe小组完成[12,54-56],这些结果进一步完善了微分电导率的研究方法,一篇较为系统总结微分电导率研究方法的综述见文献[3].

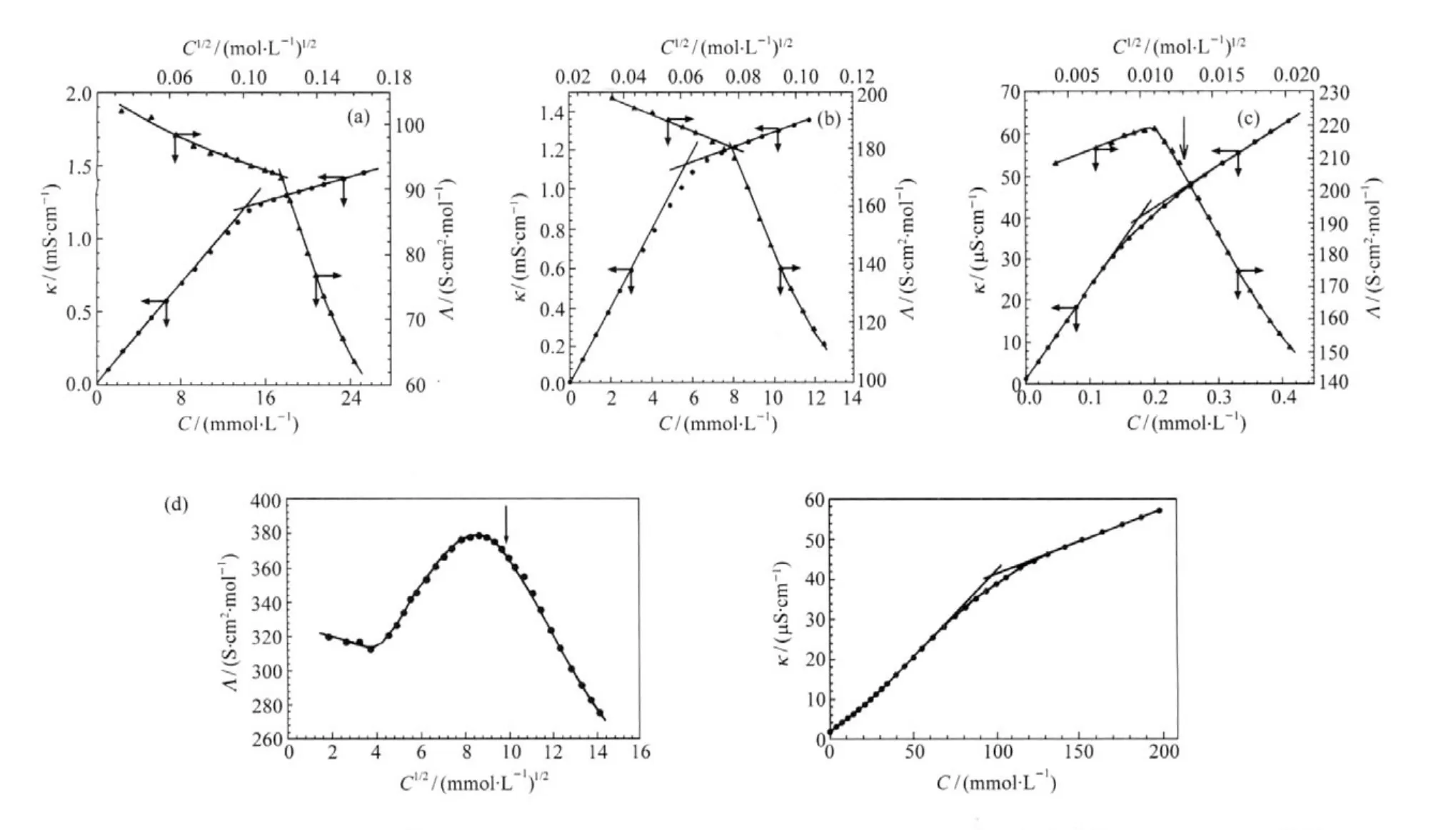
图8 C12TABr(a)、Gemini表面活性剂10-3-10(b)、14-8-14(c)和16-xylyl-16(d)水溶液的κ-C和Λ-C1/2曲线[35]Fig.8 Specific conductivity and molar conductivity plots for C12TABr(a),Gemini surfactant 10-3-10(b), 14-8-14(c)and 16-xylyl-16(d)aqueous solutions[35]

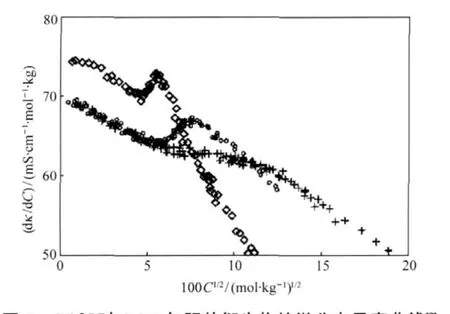
图9 25℃时AOT与胆盐衍生物的微分电导率曲线[3]Fig.9 Differential conductivity plots at 25℃for AOT and the derivatives of bile salt[3] (◇)AOT,(○)NaTDC,(+)NaTUDC

如第3节所述,预聚集的小聚集体其反离子是完全电离的,从而表现出强电解质的行为.相比完全电离的单体(没有发生低聚化),由于小聚集体荷电多,在电场下离子迁移率要高于单体离子.微分电导率作为单位浓度下的电导,正比于离子的迁移率,因而小聚集体的生成将导致微分电导率信号增加.从dκ/dC-C1/2曲线看,如果没有预胶束化行为,在低浓度区域其dκ/dC应随着浓度增大而略有下降(图9),但出现预胶束化后,曲线反而出现上升,直至达到正常的cmc时,曲线才开始再次呈现近乎线性的下降,这对应了胶束数目随浓度的增多[3].由此可见,从溶液的dκ/dC-C1/2曲线在低浓度区域是否出现极大点可以判断有没有发生预胶束化现象.图9给出AOT、NaTDC(sodium taurodeoxycholate)、NaTUDC(sodium tauroursodeoxychaolate)的微分电导率曲线[3],其中AOT和NaTDC在初始降低后开始增加,出现了明显的极大点,这意味着形成了多电荷的聚集体(multi-charged aggregates),即发生了预胶束化现象.与摩尔电导率相比,微分电导是判定预胶束的更直接方法,这为当前关注的Gemini表面活性剂(由于分子间的强烈相互作用常出现预胶束化现象)自组织研究提供了很好的方法.

6 预胶束聚集数的微分电导率预测

在稀溶液范围,根据微分电导率的定义,其初始线性下降的直线可以外推到浓度为零,其截距(κ/C)即为在无限稀溶液时单体的摩尔电导率Λf0(在电导率测量中浓度单位通常采用mol·kg-1).类似地,如果有预聚集的话,也可以外推极大值之后下降的直线至浓度为零,从截距可得无限稀溶液时小聚集体(预胶束)的摩尔电导率Λa0,根据无限稀释时的Kohlrausch定律,有

式中λf0、λa0和λg0分别为表面活性剂单体离子、预胶束离子和反离子的摩尔电导率.由于λg0(反离子)可由数据表中查到,这样可以根据实验测定的Λf0和Λa0求算λf0和λa0.

假设表面活性剂离子和预胶束离子均为球形粒子,其半径分别为rf和ra,忽略表面活性剂离子在低聚化过程的体积改变,那么预胶束的聚集数可近似估算为

Stokes定律给出了荷电球形粒子的倘度(单位电位梯度下的离子速率)Uf(表面活性剂离子)和Ua(预胶束离子)分别为

式中η为溶剂粘度,e为单元电荷.假设预胶束荷有Z个电荷,由于预胶束是完全解离的,于是有Z=N.根据电化学知识,有λ=FU(F为Faraday常数),因此

由式(8)有(ra/rf)=N1/3,代入上式整理得

由此,依据以上方法得到λf0和λa0后,代入式(14)可估算预胶束的聚集数.

上述方法只是简单的估计,由于通常的荧光探针法尚无法得到预胶束的聚集数[57-58],因此可以作为了解预胶束尺寸的一种参考.

7 总结

作为表征表面活性剂自组织能力的重要参数,临界胶束浓度cmc对理解其性能至关重要,利用Carpena发展的方法可正确提取cmc,这个数学方法也适用于处理芘探针的I1/I3-C曲线以获得cmc.预胶束是分子间强相互作用的表面活性剂体系常见的行为,摩尔电导率和微分电导率法可给出预胶束的信息,尤其是后者甚至可以估计预胶束的聚集数.总结可见电导率法能够灵敏地响应离子型表面活性剂在溶液中的行为,是研究它们在水溶液中自组织行为的重要方法.

1 Zana,R.Surfactant solutions,new methods of investigation.Trans. Tang,S.T.;Cheng,S.J.Beijing:Petroleum Industry Press,1992: 221-270 [Zana,R.表面活性剂溶液研究新方法.唐善驮,程绍进,译.北京:石油工业出版社,1992:221-270]

2 Zana,R.J.Colloid Interface Sci.,2002,248:203

3 Manabe,M.The differential conductivity technique and its application to mixed surfactant solutions for determining ionic constants//Abe,M.;Scamehorn,J.F.Mixed surfactant systems. 2nd ed.New York:Marcel Dekker,2005:Chapter 3

4 Rosen,M.J.;Surfactants and interfacial phenomena.2nd ed.New York:John Wiley&Sons Inc.,1988

5 Zana,R.Langmuir,1996,12:1208

6 Zheng,Y.Y.;Zhao,J.X.;Zheng,O.;You,Y.;Qiu,Y.Acta Chimica Sinica,2001,59(5):690 [郑玉婴,赵剑曦,郑 欧,游 毅,邱 羽.化学学报,2001,59(5):690]

7 Bai,G.;Wang,J.;Wang,Y.;Yan,H.J.Phys.Chem.B,2002,106: 6614

8 Wang,X.;Wang,J.;Wang,Y.;Ye,J.;Yan,H.;Thomas,R.K. J.Phys.Chem.B,2003,107:11428

9 Rubingh,D.N.Mixed micelle solutions//Mittal,K.L.Solution chemistry of surfactants.Vol.1.New York:Plenum,1979:337-354

10 Rosen,M.J.;Hua,X.Y.J.Colloid Interface Sci.,1982,86:164

11 Hua,X.Y.;Rosen,M.J.J.Colloid Interface Sci.,1982,90:212

12 Manabe,M.;Kawamura,H.;Yamashita,A.;Tokunaga,S. J.Colloid Interface Sci.,1987,115:147

13 Sugihara,G.;Era,Y.;Funatsu,M.;Kunitake,T.;Lee,S.;Sasaki,Y. J.Colloid Interface Sci.,1997,187:435

14 Fujiwara,M.;Okano,T.;Nakashima,T.H.;Nakamura,A.A.; Sugihara,G.Colloid Polym.Sci.,1997,275:474

15 Sugihara,G.;Nakamura,A.A.;Nakashima,T.H.;Araki,Y.I.; Okano,T.;Fujiwara,M.Colloid Polym.Sci.,1997,275:790

16 Ruiz,C.C.Colloid Polym.Sci.,1999,277:701

17 Carcía-Mateos,I.;Velázquez,M.M.;Rodríguez,L.J.Langmuir, 1990,6:1078

18 Zhao,J.;Christian,S.D.;Fung,B.M.J.Phys.Chem.B,1998, 102:7613

19 Pérez-Rodríguez,M.;Prieto,G.;Rega,C.;Varela,L.M.; Sarmiento,F.;Mosquera,V.Langmuir,1998,14:4422

20 Phillips,J.N.Trans.Faraday Soc.,1955,51:561

21 Williams,R.J.;Phillips,J.N.;Mysels,K.J.Trans.Faraday Soc., 1955,51:728

22 Carpena,P.;Aguiar,J.;Bernaola-Galván,P.;Ruiz,C.C.Langmuir, 2002,18:6054

23 Hirata,H.;Hattori,N.;Ishida,M.;Okabayashi,H.;Frusaka,M.; Zana,R.J.Phys.Chem.,1995,99:17778

24 Quagliotto,P.;Viscardi,G.;Barolo,C.;D′Angelo,D.;Barni,E.; Compari,C.;Duce,E.;Fisicaro,E.J.Org.Chem.,2005,70:9857

25 Pei,X.M.;Zhao,J.X.;Jiang,R.Colloid Polym.Sci.,2010,288: 711

26 Quagliotto,P.;Barbero,N.;Barolo,C.;Costabello,K.;Marchese, L.;Coluccia,S.;Kalyanasundaram,K.;Viscardi,G.Dyes Pigments, 2009,82:124

27 Treiner,C.;Makayssi,A.Langmuir,1992,8:794

28 Graciani,M.D.;Rodríguez,A.;Moyá,M.L.J.Colloid Interface Sci.,2008,328:324

29 Evans,H.C.J.Chem.Soc.,1956,117:579

30 Zhao,J.X.;Zheng,O.Chemistry,2002,65:w04 [赵剑曦,郑 欧.化学通报,2002,65:w046]

31 Ge,X.Y.;Guo,R.;Yan,P.Q.J.Normal Univ.Yangzhou,1991, 11(4):34 [葛秀英,郭 荣,严鹏权,扬州师院学报,1991,11 (4):34]

32 Yan,P.Q.;Guo,R.;Shen,M.;Li,W.;Chen,H.Y.Acta Phys.-Chim.Sin.,1994,10:175 [严鹏权,郭 荣,沈 明,李 伟,陈海燕.物理化学学报,1994,10:175]

33 Corrin,M.L.;Harkins,W.D.J.Am.Chem.Soc.,1947,69:683

34 Zhao,G.X.;Zhu,B.Y.Principles of surfactant action.Beijing: China Light Industry Press,2003:264 [赵国玺,朱瑶.表面活性剂作用原理.北京:中国轻工业出版社,2003:264]

35 Zana,R.J.Colloid Interface Sci.,2002,246:182

36 Tsubone,K.;Arakawa,Y.;Rosen,M.J.J.Colloid Interface Sci., 2003,262:516

37 Jiang,Y.C.;Wu,S.K.Acta Chim.Sin.,1990,48:447 [姜永才,吴世康.化学学报,1990,48:447]

38 Jiang,Y.C.;Shen,S.L.;Wu,S.K.Acta Chim.Sin.,1991,49:32 [姜永才,沈世龙,吴世康.化学学报,1991,49:32]

39 Jiang,Y.C.;Ye,J.P.;Wu,S.K.Acta Chim.Sin.,1992,50:1080 [姜永才,叶建平,吴世康.化学学报,1992,50:1080]

40 Jiang,Y.C.;Wu,S.K.Acta Phys.-Chim.Sin.,1994,10:381 [姜永才,吴世康.物理化学学报,1994,10:381]

41 Hadgiivanova,R.;Diamant,H.J.Phys.Chem.B,2007,111:8854

42 Menger,F.M.;Littau,C.A.J.Am.Chem.Soc.,1991,113:1451

43 Menger,F.M.;Littau,C.A.J.Am.Chem.Soc.,1993,115:10083

44 Song,L.;Rosen,M.J.Langmuir,1996,12:1149

45 Rosen,M.J.;Mathias,J.H.;Davenport,L.Langmuir,1999,15: 7340

46 Mathias,J.H.;Rosen,M.J.;Davenport,L.Langmuir,2001,17: 6148

47 Pinazo,A.;Wen,X.;Perez,L.;Infante,M.R.;Franses,E.I. Langmuir,1999,15:3134

48 Yoshimura,T.;Nyuta,K.;Esumi,K.Langmuir,2005,21:2682

49 Laschewsky,A.;Wattebled,L.;Arotcaréna,M.;Habib-Jiwan,J.L.; Rakotoaly,R.H.Langmuir,2005,21:7170

50 Jiang,Y.;Chen,H.;Cui,X.H.;Mao,S.Z.;Liu,M.L.;Luo,P.Y.; Du,Y.R.Langmuir,2008,24:3118

51 Barbero,N.;Quagliotto,P.;Barolo,C.;Artuso,E.;Buscaino,R.; Viscardi,G.Dyes Pigments,2009,83:396

52 Sakai,T.;Kaneko,Y.;Tsujii,K.Langmuir,2006,22:2039

53 Mukerjee,P.;Yang,A.Y.S.J.Phys.Chem.,1976,80:1388

54 Manabe,M.;Tokunaga,A.;Kawamura,H.;Katsuura,H.;Shiomi, M.;Hiramatsu,K.Colloid Polym.Sci.,2002,280:929

55 Manabe,M.;Funamoto,M.;Kohgami,F.;Kawamura,H.; Katsuura,H.Colloid Polym.Sci.,2003,281:239

56 Manabe,M.;Kaneko,M.;Miura,T.;Akiyama,C.;Kawamura,H.; Katsuura,H.;Shiomi,M.Bull.Chem.Soc.Jpn.,2002,75:1967

57 Zana,R.Langmuir,2002,18:7759

58 Mathias,J.H.;Rosen,M.J.;Davenport,L.Langmuir,2002,18: 7761

June 7,2010;Revised:July 14,2010;Published on Web:September 8,2010.

Conductivity for the Investigation of Ionic Surfactants in an Aqueous Solution and Some Characteristic Parameters

ZHAO Jian-Xi
(Institute of Colloid Interface Chemistry,College of Chemistry and Chemical Engineering, Fuzhou University,Fuzhou 350108,P.R.China)

Conductivity is important in the investigation of the micellization behavior of ionic surfactants in an aqueous solution.We review this sensitive technique and discuss methods to determine the critical micelle concentration (cmc)and the degree of dissociation of the micelle(α)in detail.We also investigate a special situation analysis for conductivity curves and premicellar behavior.This method is useful for the investigation of surfactant systems in which strong intermolecular interactions occur.

Ionic surfactant; Conductivity; Characteristic parameters

O648

*Corresponding author.Email:jxzhao.colloid@fzu.edu.cn;Tel:+86-591-22866338.

The project was supported by the National Natural Science Foundation of China(20673021,20873024).

国家自然科学基金(20673021,20873024)资助项目