线性二层规划扩展KT方法研究

吕一兵

(长江大学信息与数学学院，湖北 荆州 434023)

线性二层规划扩展KT方法研究

吕一兵

(长江大学信息与数学学院，湖北 荆州 434023)

为了更好地解决上层带有任意线性约束的线性二层规划问题，Shi Chenggen提出了能够求解更广泛线性二层规划问题的扩展KT方法。具体介绍了求解线性二层规划的原KT方法以及扩展KT方法，同时给出了一个用扩展KT方法和用原KT方法可以得到不同最优解的算例。算例结果表明，对有些线性二层规划问题，扩展KT方法能够得到与原KT方法不同的最优解。提出了2种KT方法的等价性条件。算例结果证实了上述等价性条件的正确性。

线性二层规划;KT方法;等价性

二层规划是二层决策问题的数学模型，它是一种具有二层递阶结构的系统优化问题。在二层规划模型中, 上层问题和下层问题都有各自的目标函数和约束条件。上层问题的目标函数和约束条件不仅与上层决策变量有关，而且还依赖于下层问题的最优解，而下层问题的最优解又受到上层决策变量的影响。人们在上世纪70年代开始对二层规划进行研究以来，无论在理论方面还是在算法研究方面都取得了很大的成绩，然而二层规划问题是NP-难问题[1]，因此对二层规划的研究大多数还局限于线性二层规划。即便如此，Shi Chenggen指出[2]，人们一致认可的线性二层规划最优解定义在处理上层带有任意线性约束形式的线性二层规划问题时还存在缺陷。为了解决存在的缺陷，Shi Chenggen给出了线性二层规划最优解的新定义，并且在新定义的基础上Shi Chenggen给出了求解线性二层规划的扩展KT方法[3]。同时Shi Chenggen指出扩展的KT方法相比原来的KT方法能够解决更为广泛的线性二层规划问题。

虽然Shi Chenggen提出的求解线性二层规划的扩展KT方法能够解决原KT方法的不足，但是并不是能够解决比原KT方法更广泛的线性二层规划问题。事实上，对于某些线性二层规划问题，用扩展KT方法所得到最优解有可能与用原KT方法得到的最优解不相同，出现这种情况就比较容易造成实际应用的混乱。因此研究2种求解线性二层规划的KT方法之间的关系就显得十分必要。为此，笔者具体介绍了求解线性二层规划的原KT方法以及扩展KT方法，同时给出了一个用扩展KT方法和用原KT方法可以得到不同最优解的算例，并提出了求解线性二层规划的2种KT方法之间的等价性条件。

1 问题的提出

假设：x∈X⊂Rn;y∈Y⊂Rm分别是上、下层决策变量,F、f:Rn×Rm→R1分别是上、下层目标函数。线性二层规划的一般数学模型[4]如下：

(1)

式中，c1,c2∈Rn；d1,d2∈Rm；b1∈Rp；b2∈Rq；A1∈Rp×n；A2∈Rq×n；B1∈Rp×m；B2∈Rq×m。

相应线性二层规划(1),Bard给出了如下定义[4]:

定义1(a)线性二层规划的约束域：

S={(x，y) :x∈X，y∈Y，A1x+B1y≤b1，A2x+B2y≤b2}

(b)对于x∈X，下层问题的可行域：

S(x) ={y∈Y:A2x+B2y≤b2}

(c)S在上层决策空间的投影:

S(X) = {x∈X:∃y∈Y，A1x+B1y≤b1，A2x+B2y≤b2}

(d)对于x∈S(X)，下层问题的合理反应集：

P(x) ={y∈Y:y∈argmin[f(x,y):y∈S(x)]}

(e)线性二层规划的诱导域:

IR={(x，y):(x，y)∈S，y∈P(x)}

为了保证(1)存在最优解，Bard给出如下假设[4]。

假设1(a)S为非空紧集； (b)对于x∈S(X)，下层问题的合理反应集P(x)≠Φ；(c)P(x)为一一映射。 定义1以及假设1是线性二层规划数学模型的基础，它们对线性二层规划问题算法的形成起到了关键性作用，同时也是线性二层规划最优性条件的理论基础。然而，Shi Chenggen举例指出[2]，即使线性二层规划在定义1下满足上述3条假设，也可能不存在最优解，因为即使3条假设得到满足，也无法保证线性二层规划的诱导域非空。这正是定义1的缺陷之所在。为了解决该缺陷，对线性二层规划的一般数学模型(1)，Shi Chenggen给出了如下关于线性二层规划最优解的新定义[2]。

定义2(a)线性二层规划的约束域：

S={(x，y) :x∈X，y∈Y，A1x+B1y≤b1，A2x+B2y≤b2}

(b)S在上层决策空间的投影:

S(X)={x∈X:∃y∈Y，A1x+B1y≤b1，A2x+B2y≤b2}

(c)对于x∈S(X)，下层问题的可行域：

S(x)={y∈Y:(x,y)∈S}

(d)对于x∈S(X)，下层问题的合理反应集：

P(x) ={y∈Y:y∈argmin[f(x,y) :y∈S(x)]}

(e)线性二层规划的诱导域:

IR={(x,y) :(x,y)∈S,y∈P(x)}

对于定义2, Shi Chenggen给出了下列定理[2]:

定理1如果S为非空紧集, 那么线性二层规划(1)必存在最优解。

1.1原KT方法

Bard给出的求解线性二层规划(1)的KT方法[4]，即原KT方法的主要思想是以线性二层规划下层问题的KT最优性条件代替下层问题，将线性二层规划问题(1)转化为带有互补约束的单层规划问题。假设u∈Rq,v∈Rm分别是相应于式(1)的第4个式子和y≥0的对偶变量，Bard给出了如下命题[4]。

命题1(x*,y*)是问题(1)的最优解的必要条件是存在行向量u*,v*,使得(x*,y*,u*,v*)是如下问题的最优解:

minF(x,y) =c1x+d1y

s.t.A1x+B1y≤b1

A2x+B2y≤b2

uB2-v= -d2

u(b2-A2x-B2y)+vy= 0

x≥0y≥0u≥0v≥0

(2)

式(2)是一类求解线性二层规划算法的理论基础[5]，然而Shi Chenggen给出的一个算例表明式(2)在求解上层带有任意线性约束的线性二层规划问题时存在着无法找到问题最优解的缺陷[3]。为了解决这种缺陷，Shi Chenggen在定义2的基础上，给出了求解线性二层规划的扩展KT方法。

1.2扩展KT方法

扩展KT方法的基本思想是在定义2的基础上，以下层问题的KT最优性条件代替下层问题，从而得到相应的单层规划。Shi Chenggen给出并证明了如下命题[3]:

命题2(x*,y*)是问题(1)的最优解的充要条件是存在行向量u*∈Rp,v*∈Rq,w*∈Rm,使得(x*,y*,u*,v*,w*)是如下问题的最优解:

minF(x,y) =c1x+d1y

s.t.A1x+B1y≤b1

A2x+B2y≤b2

uB1+vB2-w= -d2

u(b1-A1x-B1y)+v(b2-A2x-B2y)+wy= 0

x≥0y≥0u≥0v≥0w≥0

命题2是扩展KT方法的理论基础， 同时Shi Chenggen指出， 扩展KT方法相比原KT方法能够解决更为广泛的线性二层规划问题[3]。

1.3反例

然而，对有些线性二层规划问题，利用扩展KT方法与原KT方法可以得到不同的最优解。这种情况可以通过下面的例子予以说明。

例1考虑如下线性二层规划问题,其中x∈R1，y∈R1，X={x|x≥0}，Y={y|y≥0}。

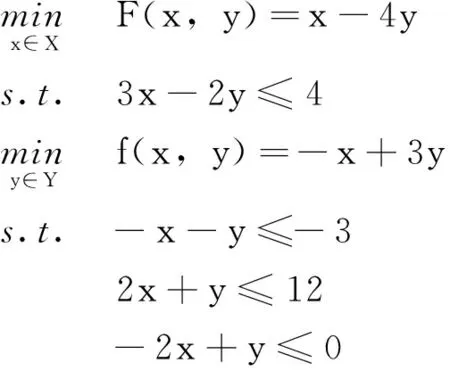
(3)

首先用原KT方法， 即命题1去求解例1。

令：

g1(x,y)=x+y-3≥0g2(x,y) =12-2x-y≥0g3(x,y)=2x-y≥0

式(3)可以相应的转化为：

minF(x,y)=x-4y

s.t. 3x-2y≤4

-x-y≤-3

2x+y≤12

-2x+y≤0

-u1+u2+u3-v=-3

u1g1(x,y)+u2g2(x,y)+u3g3(x,y)+uy=0

x≥0y≥0u1≥0u2≥0u3≥0v≥0

(4)

可以分2种情况进行讨论：

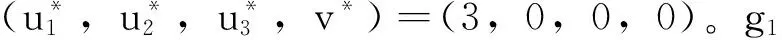
minx-4y

s.t. 3x-2y≤4

-x-y=-3

2x+y≤12

-2x+y≤0

x≥0y≥0

利用单纯形方法，可以得到最优解为(x*,y*) = (1，2)。

minx-4y

s.t. 3x-2y≤4

-x-y=-3

2x+y≤12

-2x+y≤0

x≥0y=0

利用单纯形算法，可知上述问题不可行。

由上述2种情况可知用原KT方法求解例1，得到的最优解为(x*，y*)=(1，2)。

其次用扩展KT方法,即利用命题2求解例1。类似于文献[3]的求解过程， 可以得到用扩展KT方法求解例1的最优解为(x*，y*)= (4,4)。

从上面的例子可以看到，对于例1，2种KT方法得到了2个不同的最优解。这表明虽然扩展KT方法可以解决原KT方法存在的不足[3]，但是对有的线性二层规划问题，扩展KT方法可以得到与原KT方法不同的结果。出现这种情况显然会造成实际应用的混乱。因此，研究2种KT方法之间的关系就显得十分必要。

2 扩展KT方法和原KT方法之间的等价条件

由前所述，求解线性二层规划的KT方法的基本思想是以下层问题的KT最优性条件代替下层问题。导致2种KT方法对同一个线性二层规划问题得到不同最优解的原因在于定义1与定义2有不同的下层问题可行域定义。因此，要研究2种KT方法之间的关系，只需要研究2种定义(定义1与定义2)下的下层问题之间的关系。

2.1等价性条件

下面指出当线性二层规划(1)满足一定条件时，2种定义下的下层问题是等价的。此时对该类线性二层规划问题，2种KT方法可以得到相同的最优解。在给出结果之前,为方便起见先介绍2个有用的记号：

P1(x):定义1下线性二层规划(1)的下层问题的合理反应集

P2(x):定义2下线性二层规划(1)的下层问题的合理反应集

命题3假设对于x∈S(X),满足(x,P1(x))∈S,那么线性二层规划(1)的下层问题在x∈S(X)的条件下与下列线性规划问题有相同的最优解:

(5)

证明由P1(x)的定义可知，对x∈S(X)，P1(x)为下列线性规划之最优解：

(6)

由于(x,P1(x))∈S，则对于x∈S(X)，P1(x)同样为式(5)的最优解。

另一方面,假设对于x∈S(X)，式(5)的最优解为P2(x),显然有(x，P2(x))∈S。现在要证明对于x∈S(X)，P2(x)同样为式(6)的最优解。不妨假设对于x∈S(X)，式(6)的最优解为y*≠P2(x)。由上面的证明可知对于x∈S(X)，y*为式(5)的最优解。这就与对于x∈S(X)，式(5)的最优解为P2(x)相矛盾。矛盾表明对于x∈S(X)，P2(x)也为式(6)的最优解。这样就完成了命题的证明。

下面在命题3的基础上给出2种KT方法之间的等价性关系。

定理2若线性二层规划(1)满足约束域S为非空紧集，且x∈S(X),(x，P1(x))∈S，那么对于线性二层规划(1)，原KT方法与扩展KT方法可以得到相同的最优解。

证明 由命题3可知，对于x∈S(X),若(x，P1(x))∈S,那么线性二层规划(1)的下层问题与式(5)具有相同的最优解。也就是说线性二层规划(1)等价于下列线性二层规划:

再由命题1以及命题2可知定理的结论成立。证毕。

如果定理2的条件得不到满足，那么就有可能导致对同一个线性二层规划问题2种KT方法可以得到不同的最优解。如在例1中， 对于3≤x′≤4,P1(x′)=0。显然(x′，P1(x′)∉S，这也导致例1在2种KT方法下得到了不同的最优解。而如果下层问题的合理反应集P1(x)满足(x,P1(x))∈S，那么对该类线性二层规划问题用2种KT方法可以得到相同的最优解。

2.2算例

例2考虑下列线性二层规划问题，其中x∈R1,y∈R1,X= {x|x≥0},Y={y|y≥0}。

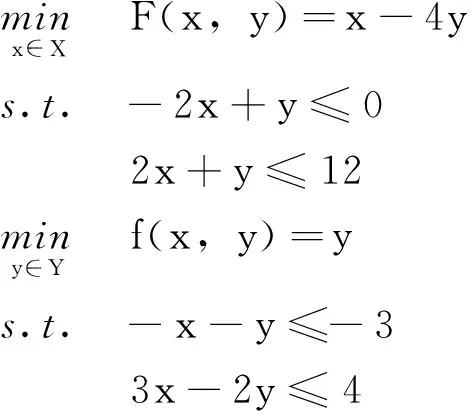
(7)

对于问题(7)，S(X) ={1≤x≤4},可以得到：

容易验证(x,P1(x))∈S，定理1的假设条件得到满足。那么问题(7)在2种KT方法下应该有相同的最优解。事实上类似于例1的求解过程2种KT方法可以得到相同的最优解为(x*,y*) = (4，4)。

3 结 语

对Shi Chenggen提出的扩展KT方法进行了讨论,举出的一个反例表明扩展的KT方法虽然可以解决原方法的不足,但是并不是能够解决更广泛的线性二层规划问题。在反例的基础上,提出了2种KT方法的等价性条件,即对于x∈S(X),有(x，P1(x))∈S,那么线性二层规划在2种KT方法下可以得到相同的最优解。值得指出的是对于x∈S(X),如何判别(x，P1(x))∈S是个值得继续研究的问题。而如果能够得到比较简单的判别方法，那么在(x，P1(x))∈S的前提下就可以尽量将下层约束问题移到上层，以简化下层约束问题。这样对构造求解线性二层规划的有效算法(如分枝定界法) 是有意义的。

[1]Ben-Ayed O, Blair O.Computational diffculity of bilevel linear programming[J].Operations Research, 1990,38:556～560.

[2] Shi Chenggen, Zhang Guangquan, Lu Jie. On the definition of linear bilevel programming solutin[J]. Applied Mathematics and Compution, 2005,160:169～173.

[3] Shi Chenggen, Zhang Guangquan, Lu Jie. An extended Kuhn-Tucker approach for linear bilevel programming[J]. Applied Mathematics and Compution, 2005,162:51～63.

[4] Bard J F. Practical Bilevel Optimization: Algorithms and Application[M]. The Netherlands:Kluwer Academic Publisher, 1998.

[5] Hansen P, Jaumard B, Savard G. New branch-and-bound rules for linear bilevel programming[J]. SIAM Journal on Science and Statistical Computing, 1992,13:1194～1217.

[6]Liu X, Wang R, Wang Sh. An algorithm to solve linear bilevel programming[J]. Journal of Systems Science and Systems Engineering, 1995,4(2):158～167.

[7] Marcotte P, Savard G. A note on the Pareto optimality of solutions to the linear bilevel programming problem[J]. Computers and Opertiond Research, 1991,18:355～359.

[编辑] 洪云飞

O224

A

1673-1409(2010)01-N001-05