简述极小值点与三角形内心相关的点函数

●

(华南师范大学数学科学学院 广东广州 510631)

简述极小值点与三角形内心相关的点函数

●黎海燕吴康

(华南师范大学数学科学学院 广东广州 510631)

几何极值是竞赛数学的热点问题之一，很多专家、教师都研究过大量的几何极值问题，总结了很多求解方法.其实，除了各式各样的求几何极值的方法外，其中蕴含着的美妙性质更是值得我们去探究.研究发现不少点函数(设P为非空点集，若按照某种确定的对应关系f，即对于集合P中任意一点A，在实数集R中都有唯一确定的数y与之对应，则称f:P→R为从点集到实数集R的一个函数，简称点函数)的极小值点恰为圆外切多边形的内心.

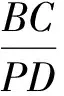
(第22届IMO试题)

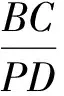
图1

推广1如图1，在四边形ABCD中，AB=a+b,BC=b+c,CD=c+d,DA=d+a.四边形ABCD内一点P，点P到AB，BC，CD，DA各边的距离分别为x,y,m,n，使得函数

取极小值的点P为四边形ABCD的内心.

证明因为

∠A+∠B+∠C+∠D+2∠1+

2∠2+2∠3+2∠4=4π，

所以

∠1+∠2+∠3+∠4=π，

即

∠GOE+∠GFE=π.

同理可证

∠FGO+∠FEO=π，

于是点O，E，F，G共圆.设圆心为I，线段OG的中点为H，连结AH，IH，则

AH⊥GO,IH⊥GO，

所以点A，H，I共线.因为AO=AG，所以AI为∠A的角平分线.同理可证BI，CI，DI分别为∠B,∠C,∠D的角平分线，所以四边形ABCD的内心存在，为点I.设∠PAB=α,∠PBC=β,∠PCD=γ，∠PDA=δ，由

AB=x·cotα+x·cot(B-β),
BC=y·cotβ+y·cot(C-γ)，
CD=m·cotγ+m·cot(D-δ),
DA=n·cotδ+n·cot(A-α)，

得

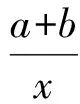
cotα+cos(A-α)+cotβ+cot(B-β)+

cotγ+cot(C-γ)+cotδ+cot(D-δ).

又因为

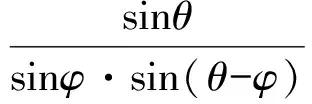
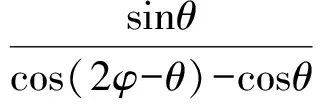
所以

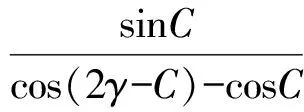
当且仅当2α=A,2β=B,2γ=C,2δ=D，即点P为四边形ABCD的内心时，f(P)取得最小值.

证明设二面角∠A-BC-D=θ1，∠A-CD-B=θ2,∠A-BD-C=θ3,∠C-AB-D=θ4,∠B-AC-D=θ5,∠B-AD-C=θ6,∠P-BC-D=α1,∠P-BD-C=α2,∠P-CD-B=α3,∠P-AC-D=β1,∠P-AD-C=β2,∠P-AB-C=γ.由

2S1=BC·h1·cotα1+BD·h1·cotα2+

CD·h1·cotα3,

2S2=CD·h2·cot(θ2-α3)+AC·h2·cotβ1+

AD·h2·cotβ2,

2S3=BD·h3·cot(θ2-α2)+AD·h3·cot(θ6-β2)+

AB·h3·cotγ,

2S4=BC·h4·cot(θ1-α1)+AB·h4·cot(θ4-γ)+

AC·h4·cot(θ5-β1).

类似推广1,可得

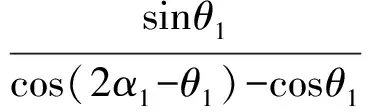
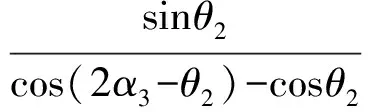
当且仅当2α1=θ1,2α2=θ3,2α3=θ2,2β1=θ5,2β2=θ6,2γ=θ4，即点P为四面体A-BCD的内心时，f(P)取得极小值.

除了在与几何极值相关的问题中可挖掘大量极小值点恰为圆外切多边形内心的点函数，在与图形内心相关的恒等式中，常常也可以构造出相应的以图形内心为极小值点的点函数，因此按照此研究思路可以发现更多类似的点函数，例如以下定理和推论.

定理1△ABC内任一点到3个顶点的距离分别为x,y,z,使得函数f(P)=ax2+by2+cz2取得极小值的点P为△ABC的内心.

证明由于在△ABC中，平面内任意一点P到内心I的距离[1]为

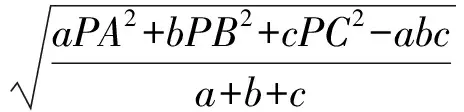
f(P)=(a+b+c)F2(P)+abc.

当F(P)取得极小值时，f(P)取得极小值.由于F(P)的极小值为F(I)=0，因此使f(P)取得极小值的点P为△ABC的内心.

图2

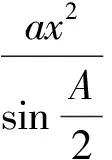
证明如图2,设△ABC的内心为I，与顶点A，B，C相对的旁心分别为Ia,Ib,Ic，AI，BI，CI分别与△ABC外接圆相交于点A1,B1,C1，则

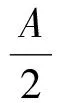
因为a=2RsinA,b=2RsinB,c=2RsinC,

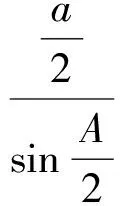
由B1Ib=B1I,C1Ic=C1I,A1Ia=A1I[2]，得

IbIc=2B1C1,IaIc=2A1C1,IaIb=2A1B1,

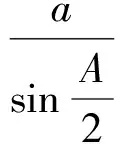
由推论2得

取得极小值的点P为△ABC旁心三角形的内心.

[1] 刘黎明.三角形内心的性质和心距公式[J].中学数学，1996(2):45-47.

[2] 胡耀宗.涉及三角形旁心的几何命题[J].益阳师专学报，1994,10(5):37-39.