聚焦空间坐标系的合理建立

●

(吉水中学 江西吉水 331600)

聚焦空间坐标系的合理建立

●孙春生

(吉水中学 江西吉水 331600)

空间坐标系建立的合理与否，不仅直接关系到空间点坐标求法的繁简，而且好的坐标系更能凸现图像的实质，更深入地把握问题的本质．本文结合近几年高考试题中的各类情形，谈谈空间坐标系的合理建立．

空间坐标系的建立可分为以下几类:

(1)图形中有3条两两垂直相交的直线．常以这3条两两垂直的直线分别作坐标轴，以交点为坐标原点建立空间坐标系.

(2008年江西省数学高考试题)

分析由题意知，侧棱OA，OB，OC两两垂直，因此可考虑将3条侧棱的交点O作原点建立空间坐标系．

图1

图2

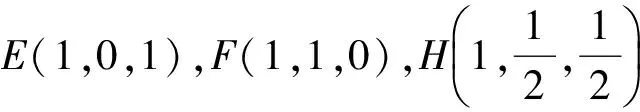
解得z=3,即B1(0,0,3).同理可得,C1(0,3,0)．

评注出现不直观的3条两两垂直的相交直线时,可将坐标原点置于3条线的交点处.在建立坐标系时,要注意使用右手法则,并根据条件求出一些不太明显的空间点的坐标.

(2)图形中没有两两垂直的3条直线，但出现线面垂直的图形，常以垂线或与垂线平行的某直线作为一条坐标轴，再依据图形考虑垂面上另2条相互垂直的直线作为坐标轴.

(2009年安徽省数学高考试题)

分析AE，CF都与平面ABCD垂直，因此可将坐标原点置于点A处(或点C处)，以AE为z轴,以AC为y轴建立坐标系；考虑到四边形ABCD是菱形,也可将坐标原点置于AC的中点，以AC与BD为坐标轴建立坐标系．

图3

图4

评注空间坐标系的建立,一般要考虑尽量地将各点的坐标置于坐标轴上.这样建成的坐标系能较快地把各点坐标表示出来,再者能为后续的问题减少运算量.

(3)图形中没有两两垂直的3条直线，但出现面面垂直的关系，常根据面面垂直的性质定理，将空间坐标原点置于两垂面的交线上.

例3如图5，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E,F,O分别为PA，PB，AC的中点，G是OC的中点,AC=16，PA=PC=10.试建立合适的空间坐标系，并求出图中所有点的坐标．

(2009年浙江省数学高考试题)

分析由于△ABC是以AC为斜边的等腰直角三角形,因此由面面垂直的性质定理知,OB⊥平面PAC.同理可得,OP⊥平面BAC,于是OB,OC,OP两两垂直.

图5

图6

解如图6，连结OP.以点O为坐标原点，分别以OB，OC，OP所在直线为x轴，y轴，z轴，建立空间直角坐标系O-xyz，则O(0，0，0),A(0，-8，0)，B(8，0，0)，C(0，8，0)，P(0，0，6).又E,F,G的分别为相应线段的中点,所以

E(0，-4，3)，F(4，0，3)，G(0，4，0).

评注坐标系的建立要有一定的空间几何知识作背景.有许多问题是先利用空间几何性质分析出一些线线垂直、线面垂直或面面垂直，再来考虑空间坐标系的合理建立的．

(4)无三线垂直相交，并且无特殊垂直关系．需要从宏观上把握图形，考虑将图形放置在我们熟知的几何图形尤其是正方体或长方体中来考察.

图7

(2006年江西省数学高考试题)

分析本例题中的图形用常规方法建立坐标系，感觉坐标原点无从安排．考虑到BD⊥DC，因此想到以点D为空间坐标系的原点，构造正方体(长方体)的模型来求解．

解作AH⊥面BCD于点H,连结BH,CH,DH,则四边形BHCD是正方形,且AH=1,以点D为原点,以DB为x轴,DC为y轴建立空间直角坐标系,如图7，则D(0,0,0),B(1,0,0)，C(0,1,0),A(1,1,1).

评注对一些特殊图形的熟练把握，有助于我们在解题时广开思路，寻求到解题捷径．

空间坐标系建立的好坏关系到解题运算量的大小，甚至是解题的成败．只有不断地进行归纳比较、分析总结，才能在遇到各类图形的情形下，找到合适方法，突破解题瓶颈．