数学问题变式教学的案例探索
●
(绍兴市第一中学 浙江绍兴 312000)
数学问题变式教学的案例探索
●虞金龙
(绍兴市第一中学 浙江绍兴 312000)
“问题是数学的心脏”.在数学教学过程中,运用不同的知识与方法变换问题的形式,从一题多解、一题多变、多题一解、一题多图、多图一解……帮助学生提出问题、分析问题、解决问题,让学生在解题过程中发展智力,提高解题能力.这样做既可以使学生学得生动活泼,又可以减轻学生的负担,培养学生的创新意识,这也正是素质教育所要求的.变式的实质是根据学生的心理特点在设计问题的过程中,创设认知和技能的最近发展区,诱发学生通过探索、求异的思维活动发展能力.笔者以向量的高三复习实践为例谈对问题变式的思考,旨在抛砖引玉.
1 寓趣于教,构造数字趣题
兴趣是带有情感色彩的认识倾向,它总是和成功的喜悦紧密相连的.构造一些具有启发性的数字趣题,对培养学生兴趣,开拓解题思路具有不可低估的作用.
有些问题是一般结论,乍看较难证明、但只要掌握题目结构,在教学时有意识地构造数字趣题,不仅会激发学生的学习热情,还会达到事半功倍的效果.例如在复习向量综合应用问题时,笔者编了以下题目.
分析依题意知{an}成等差数列,且d=3.{bn}成等比数列,得
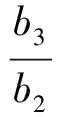
…
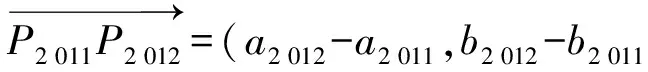
因为
an+1-an=d=3,

所以
于是

( )
A.2 010B.2 011C.2 012D.2 013
分析由条件可得
a1 008+a1 004=2,
即
a1+a2 011=2,
从而S2 011=2 011.故选B.
为巩固定理,又进行了以下变式:
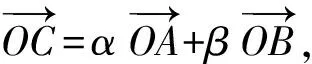
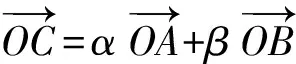
(x,y)=(2α-β,α+4β),
即
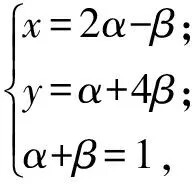
解得
x+y-3=0,
即所求的轨迹方程为直线x+y-3=0.
分析2由条件可知点A,B,C共线,即点C的轨迹为直线AB,易求AB的方程为x+y-3=0.

( )
A.点M在线段AB上
B.点B在线段AM上
C.点A在线段BM上
D.点O,A,M,B共线
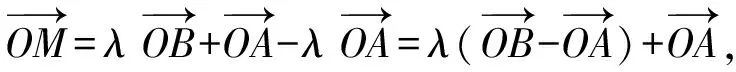
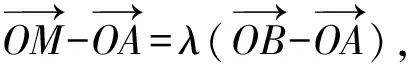

由λ∈(0,1),得点M在线段AB上.故选A.
若将例4中的条件λ∈(0,1)改为λ∈(1,2),则答案为B.
2 一题多变,提高解题能力
数学问题的一题多变能提高学生综合分析和解决问题的能力,更能激发学生学习数学的兴趣,增强求知欲.下面是笔者在复习向量时设计的一个例题,通过启发和指导,学生积极参与、共同讨论,融向量的知识于一题多变之中,取得了较好的复习效果.

( )
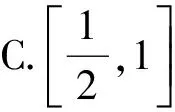

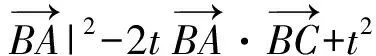
在△ABC中,易知AC=1,∠B=30°,得
2t2-3t+1≥0,
解得

故选B.
此题体现了向量的模常通过平方的方法解决.为了巩固这个知识点,笔者又将题变化如下:
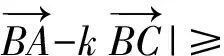
( )
A.等腰三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
分析原不等式2边平方后可化为
由k∈R得

得



从而AC为高,即∠C=90°.故选B.
3 巧编题组,培养发散思维
笔者在高三教学过程中,特别重视把有密切联系的问题编排成题组加以训练.学生在练习过程中学会了比较的方法,提高了分析、解决问题的能力.譬如在学习向量加减法的平行四边形法则和三角形法则时,编了如下问题:

( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
分析因为

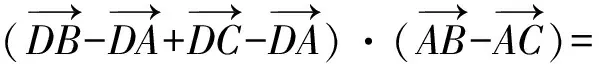

所以

由向量加减法的平行四边形法则及菱形的几何性质,知AB,AC为菱形的2条邻边,因而△ABC为等腰三角形.
为了巩固这个知识点,又编了如下题目:

分析过点P作PD⊥AC于点D,PE⊥AB于点E,则
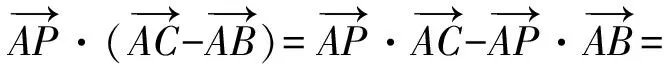
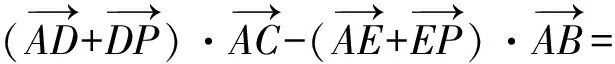
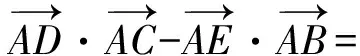

以上2道题目还体现了向量的模与平方的关系,也是解决这类问题的一个小窍门.
在数学教学中,有时可通过构造变式借题、变题,使学生耳目一新.譬如为了提高学生的编题能力,又编了以下题目:

( ).
A.40 B.200 C.10 D.0
分析由题意得
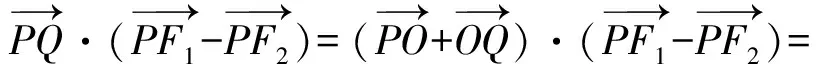
此题的解法明显体现了与前一题的一个重要共性,教师在教学时可趁热打铁.
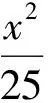
此题解法同例9完全一致,体现了编题组的优势.
同一个问题,从不同角度,用不同的知识,展示不同的“变式”.根据解题思路编排“题组”进行比较,培养学生的发散性思维.这样学生就把知识联系起来,形成整体性的认识和提高,从而达到了举一反三、触类旁通的教学效果.同时,提高了学生思维的综合能力和创造能力.但是学生在做题时,往往不重视题目中关键性的字、词、句、单位及题目后面的要求而做错了.为此,笔者还经常有意地出一些“貌似实异”的题组培养学生的审题习惯,从而提高学生思维的准确性.

