探析几何内涵 优化解题方案
●
(泗阳中学高中部 江苏泗阳 223700)
探析几何内涵优化解题方案
●刘建中
(泗阳中学高中部 江苏泗阳 223700)
很多学生在解答平面解析几何题时,由于缺乏对其几何内涵的深刻认识和有效把握,而致使解题思路狭窄,运算过程繁琐,结果常常是“会而不对”或“对而不全”.如何准确地探寻问题的几何背景与内涵,使解题过程得以优化呢?笔者根据平时的教学实践结合相关问题谈谈个人的看法,供读者参考.
1 通过几何平台的搭建寻求解法
例1如图1,F1,F2分别是双曲线x2-y2=4的左、右焦点,P为其图像右支上的一点,直线l平分∠F1PF2,过点F1作直线l的垂线,垂足为M,试求点M的轨迹方程.
分析设点M的坐标为(x,y),延长PF2,F1M交于点Q.由条件易知△PF1Q为等腰三角形,M为边F1Q的中点.又由O为F1F2的中点,得线段OM为△F1QF2的中位线,因此

所以点M的轨迹是以O为圆心,2为半径的圆,其方程是x2+y2=4.
评注先根据l平分∠F1PF2且l⊥F1M这一条件构建等腰△PF1Q,再利用三角形中位线定理和双曲线的定义,得出动点M所满足的几何关系,从而使所求的轨迹问题顺利获解.
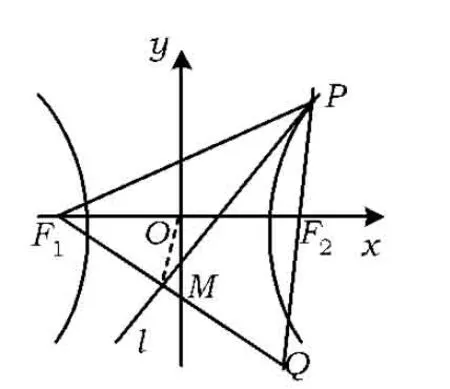
图1
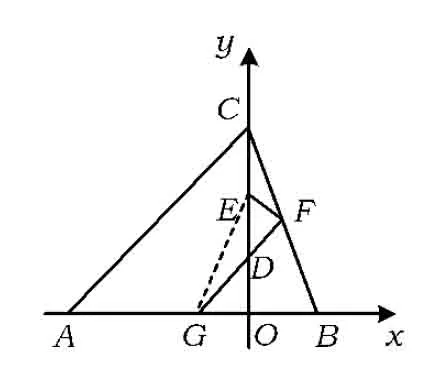
图2
2 通过几何语言的转化优化运算
例2如图2,△ABC的3个顶点坐标分别是A(-6,0),B(2,0),C(0,6),点D,E是高CO的2个三等分点,过点D作直线FG∥AC,分别交AB和BC于点G,F,连结EF.
(1)求过点E,G,F的圆M的方程;
(2)在线段AC上是否存在点H,使得过点H存在与圆M相切的直线?且当过点H有2条圆的切线HP,HQ(P,Q为切点)时,求满足∠PHQ≥90°的点H所对应轨迹的长度.
分析(1)根据条件,易得E(0,4),G(-2,0),F(1,3),则
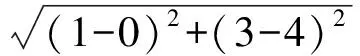
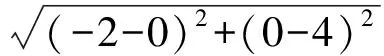
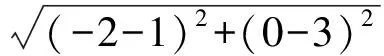
从而
EF2+FG2=EG2,
因此△EGF为直角三角形,所求圆M是以线段EG为直径的圆,其方程为
(x-0)(x+2)+(y-4)(y-0)=0,
即
x2+y2+2x-4y=0.
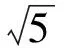
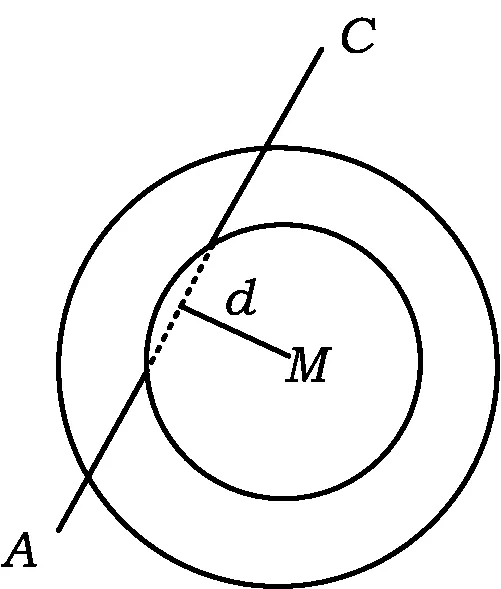
图3
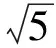
即
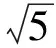
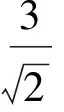

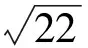

3 通过几何特征的把握巧妙探索
例3已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于点P,Q,M是PQ的中点,l与直线m:x+3y+6=0相交于点N.

图4
(1)求证:当l与m垂直时,l必过圆心C.

(3)探索AM·AN的值是否与直线l的倾斜角的大小有关.若无关,请求出其值;若有关,请说明理由.
解(1)当直线l与m垂直时,l的方程为y=3(x+1),l与y轴的交点坐标为(0,3),即l必过圆心C.

x-uy+1=0.
由点到直线距离公式得

解得

故所求直线l的方程为x+1=0或4x-3y+4=0.
(3)若l过点C,由第(1)小题知l⊥m.设垂足为H,则
若l不过点C,连结CM.由题意得CM⊥l(如图4).易证
△AMC∽△AHN,
因此

故
AM·AN=AC·AH=5,
所以AM·AN的值与直线l的倾斜角大小无关,其值为5.
评注把握当直线l过点C时这一特殊情形,利用相似三角形的相关知识,有效地避免了较为繁琐的运算,从而使探索过程轻松、顺利,事半功倍.
4 通过几何结论的运用化难为易
例4如图5,已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l:x=2.
(1)求椭圆的标准方程;
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
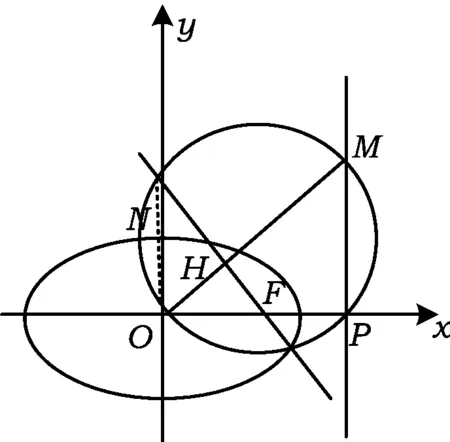
图5
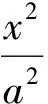

(2)设椭圆准线l与x轴的交点为P,FN与OM的交点为H,连结MN.在Rt△OMN中由OM为圆的直径,利用射影定理可得
又OM⊥FN,l⊥x轴,得点M,H,F,P共圆.由圆的割线定理可得
由式(1),式(2)得
ON2=OF·OP=1×2=2,

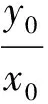
kMN·kON=-1,
进而


解析几何和平面几何研究的对象都是几何问题,区别在于研究的手段不同.在研究解析几何问题时,如果注意强化平面几何应用意识,合理地借助平面几何知识,出奇制胜,那么就能顺利地找到解题突破口,使问题得以解决.

