例说数学课堂的类比创新教学

● ●

(海盐高级中学 浙江海盐 314300) (台州市第一中学 浙江台州 318000)

例说数学课堂的类比创新教学

●王鹏锋●汤香花

(海盐高级中学 浙江海盐 314300) (台州市第一中学 浙江台州 318000)

1 问题的提出

翻开普通高中课程标准实验数学教科书，首先呈现的是教材的主编、北京师范大学刘绍学教授撰写的“主编寄语”.在这篇寄语中，刘先生对为什么要学数学，如何才能学好数学等问题提出了自己的看法，并建议：在对数学有一个正确认识的基础上，要摸索自己的学习方法学数学，做到类比地学、联系地学.既要从一般概念中看到它的具体背景，不使概念“空洞”，又要在具体例子中想到它蕴含的一般概念，以使事物有“灵魂”．在日常的数学学习中，该如何类比、联系一般概念与具体背景呢？

2 一个教学片断

不等关系与相等关系都是客观存在的基本数量关系，是数学研究的重要内容．建立不等观念、处理不等关系与处理等量问题是同样重要的．在处理问题的方式、方法上,两者是否具有相似性？学生能否利用数学内容之间的内在联系，特别是蕴含在数学知识中的数学思想方法，学习类比、推广、特殊化、化归等数学思考的常用逻辑方法，学会数学思考与推理，不断提高数学思维能力？为此，笔者设计以下题组：

1.(1)已知x=2，y=3，求x+y与x-y的值；

(2)已知x+y=5，x-y=-1，求x与y的值．

2．(1)设实数x,y满足1≤x≤2，3≤y≤4，求x+y与x-y的取值范围；

(2)设实数x,y满足4≤x+y≤6，-3≤x-y≤-1，求x与y的取值范围．

对于这2个问题，学生的看法是：第(2)小题是第(1)小题的逆运算，问题2是由问题1类比得到的，因此不等式的解题方法可以参考等式的解题方法．但在尝试解决问题时，学生们提出疑问：在等式运算中，条件与结论可以交换，但在不等式运算中，当结论变为条件时，所得结论却与原来的条件不同，解题方法正确吗？

问题意识指的是学生面临需要解决的问题时的一种清醒、自觉，并伴之以强烈的困惑、疑虑及想要去探究的内心状态．正是这种内心状态驱使着学生积极地思维，不断地产生解决问题的办法，不断地提出新的问题．

生B：类比加减消元法解方程，得到y的取值范围缩小了．

师：x与y的取值范围能继续缩小吗？

类比地学，能引发学生的学习动机，有助于学生批判性地思考，帮助学生重建知识结构．

生C：采用特值法．

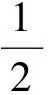
这说明生B的解答是正确的．

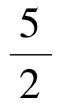
因此

1≤x-y≤3，

与已知-3≤x-y≤-1矛盾，这说明生A的解答是不正确的．

利用相等关系去分析不等关系，学生容易理解，但又产生了新的问题：在不等式的解题过程中，生A的每一个步骤都很合理，解答为什么是不正确的？

提出新的问题、新的可能性，从新的角度去看旧的问题，有助于学生联系地学，从而找到新知识的生长点．

生D：在等式中，x与y的值是确定的，可以通过代入x的值去求y的值．而在不等式中，x与y之间存在的是一种不等关系，当x取得最大(小)值时，y并不能同时取得最大(小)值．生A解法的问题正在于此，由于忽略了x与y的相互制约关系，所得出的取值范围比实际的范围要大．生B的解法整体上保持了x与y的相互制约关系，从而得出的范围是准确的．

3 体验学习方法

笔者认为，学生要获取重要的数学知识，更要体验学习数学、研究数学的方法，做到类比地学、联系地学．

3.1 问题拓展

在不等式求解过程中，必须在整体上保持x与y的相互制约关系，即根据不等式的性质，将所求代数式用已知代数式表示．因此学生容易将问题拓展为：

已知4≤x+y≤6，-3≤x-y≤-1，求3x+4y的取值范围．

解法1由

3x+4y=

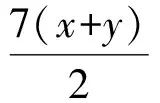
可得

解法2设3x+4y=m·(x+y)+n·(x-y)，

则

解得

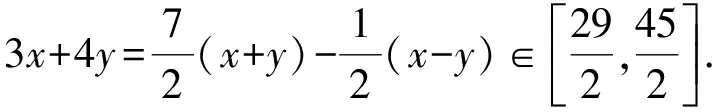
3.2 问题创新

联系等式中的运算：加、减、乘、除、乘方、开方，学生会类比不等式的加减运算性质，尝试得到不等式的乘、除、乘方、开方的运算性质，将问题创新为：

类比加减运算的解法，学生尝试将问题化归为如何在整体上保持x与y的相互制约关系，即根据不等式的性质，将所求代数式用已知代数式表示．得到如下解题过程：

因为

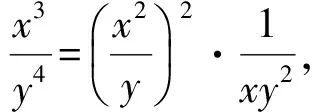
又

所以

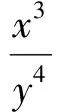
学生通过体会各种运算之间的联系与区别，总结数学学习的经验，在课堂生成中领悟数学研究的方法．

3.3 问题延伸

例1设函数f(x)=x3+3bx2+3cx有2个极值点x1,x2，且x1∈[-1,0],x2∈[1,2].

(1)求b,c满足的约束条件，并在坐标平面内画出满足这些条件的点(b,c)的区域；

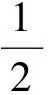
(2009年全国数学高考试题Ⅰ)

解(1)略．

(2)由题意得

又

(2)

消去b可得

因为

x2∈[1,2]，且c∈[-2,0],

所以

另解由题意得

x1+x2=-2b,x1·x2=c,

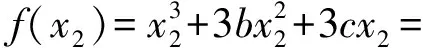
因为x1∈[-1,0],x2∈[1,2],所以