带RCE抵消策略的负顾客M／M／1工作休假排队系统

顾庆凤

（浙江林学院理学院，浙江临安 311300）

带RCE抵消策略的负顾客M／M／1工作休假排队系统

顾庆凤

（浙江林学院理学院，浙江临安 311300）

考虑服务员在休假期间不是完全停止工作，而是以相对于正常工作时低些的速率服务顾客的M／M／1工作休假排队模型.在此模型基础上，笔者针对现实的M／M／1排队模型中可能出现的外来干扰因素，提出了带RCE（Removal of Customers at the End）抵消策略的负顾客M／M／1工作休假排队这一新的模型.服务规则为先到先服务.工作休假策略为空竭服务多重工作休假.抵消原则为负顾客一对一抵消队尾的正顾客，若系统中无正顾客时，到达的负顾客自动消失，负顾客不接受服务.使用拟生灭过程和矩阵几何解方法给出了系统队长的稳态分布，证明了系统队长和等待时间的随机分解结果并给出稳态下系统中正顾客的平均队长和顾客在系统中的平均等待时间.

负顾客；工作休假；矩阵几何解；稳态分布；随机分解

1 引 言

Gelenbe在20世纪90年代初首次提出了负顾客的排队模型［3］.负顾客可以看成是某些工作的外来援助或取消信号，一般作为系统的制约因素而存在，能抵消系统中的正顾客.后来，国内外学者掀起了带有负顾客的排队模型的研究热潮.关于负顾客的排队模型的成果不断涌现［4-6］.近几年来，工作休假排队系统［7-9］也是国内外专家研究的热点，此类模型的特点是在休假时服务员不会完全停止工作，而是以一个相对来说比正常服务率低一些的速率进行工作，比如说医院系统，医院里在休假时会安排部分工作人员值班，不会让所有的医生都休息.从休假期间部分的利用系统资源的角度来说，单服务台排队的工作休假策略类似于多服务台排队的部分服务台休假策略，这可从文献［11-12］中看出.如果服务员在工作休假期间的服务率减小为零，则我们得到了经典的休假排队模型（服务员在休假期间完全停止为顾客服务，只能做些其他的辅助工作）.所以，工作休假排队是经典休假排队的扩展.受文献［4-6］的启发，笔者考虑一个将负顾客和工作休假结合起来的模型，首次提出了带RCE抵消策略的负顾客M／M／1工作休假排队系统，在RCE抵消策略下，负顾客可以看成服务系统中出现的一次外来对服务台的干扰，一次外来干扰抵消一名队尾的正顾客，当系统中没有正顾客时，外来干扰自动消失，负顾客不接受服务.该模型在日常生活中有很广泛的应用，如在通讯系统中，当数据传输到接受台时，数据传输看成正顾客的到达，外来的干扰信号看成负顾客的到达.又如在商场中，通常的顾客看成正顾客，其他商家的诱惑等因素看成负顾客.

2 模型的描述

在M／M／1工作休假排队系统中引入带RCE抵消策略的负顾客，该系统是有正、负两类顾客的单服务台系统.一旦系统内无正顾客，服务员立刻开始一个随机长度V的工作休假.在工作休假期间，服务员以低的服务率接待正顾客.若结束一次工作休假时系统中仍无正顾客，则继续一个独立同分布的工作休假.若在某次工作休假期间服务完某一个正顾客后系统中已有正顾客，则服务员终止工作休假并开始以正常服务率（更高的服务率）接待正顾客，直到服务台再次变为空闲.正顾客和负顾客均泊松到达，到达率分别为λ和ε.服务台对正顾客在正常服务期和工作休假期的服务时间均服从负指数分布，均值分别为和，这里（η＜μ）.假定到达间隔、服务时间和工作休假时间相互独立.服务规则为先到先服务.工作休假策略为空竭服务多重工作休假.抵消原则为负顾客一对一抵消队尾的正顾客（若有），若系统中无正顾客时，到达的负顾客自动消失，负顾客只起抵消正顾客的作用，负顾客不接受服务.

设工作休假时间V服从参数θ的指数分布，Qv（t）为时刻t系统中的正顾客数.

J（t）定义如下：

由于到达间隔、服务时间和工作休假时间都服从负指数分布，则｛Qv（t），J（t）｝是一个拟生灭过程（quasi birth and death process，简记QBD），有状态空间如果将状态按字典序排列后，其生成元可写成下列分块三对角形式：

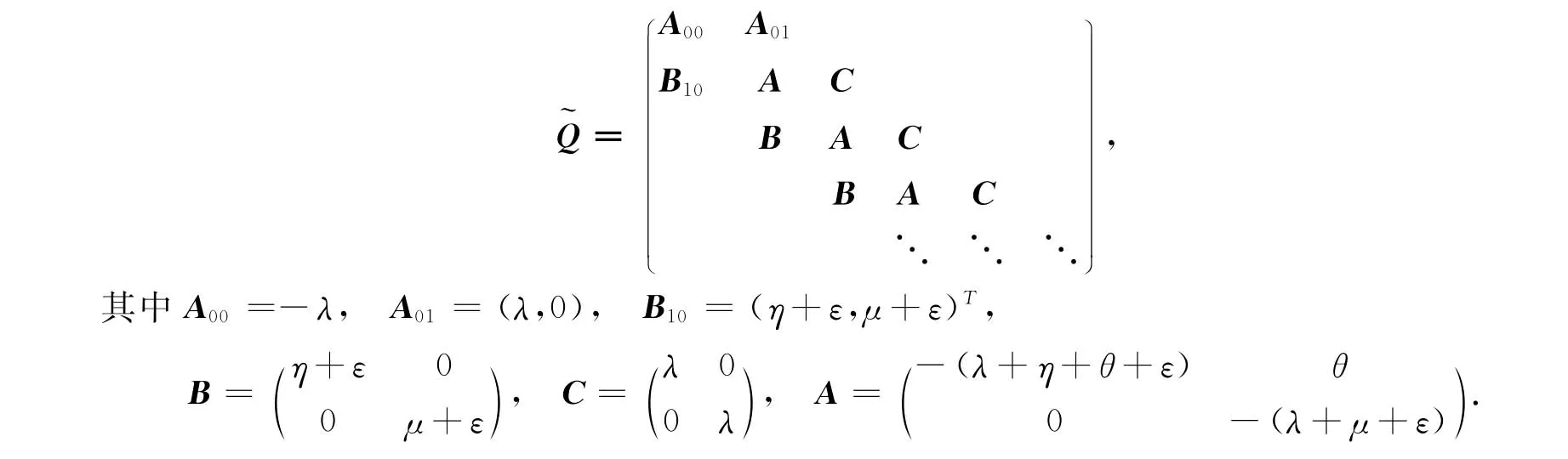
在拟生灭过程中，矩阵方程R2B＋RA＋C＝0的最小非负解R称为率阵，并起重要作用.为研究率阵R，需要下列

引理1 二次代数方程

证由（1）可知sp（R）＜1当且仅当ρ＜1.进一步地，由文献［1］定理2.4可以证明过程正常返当且仅当ρ＜1.

3 系统队长的性能指标

4 稳态队长的随机分解

5 稳态等待时间的随机分解

6 结 论

本文给出了FCFS、RCE抵消策略的负顾客M／M／1连续时间工作休假排队模型的系统队长的稳态分布和系统随机分解结果.对于RCH（Removal of Customers in the head）或两者（RCH与RCE）均有的情况，只需将文中的ε改为h（h为RCH的发生率）或ε＋h.此模型可以进一步推广到带负顾客的Geo／Geo／1离散时间工作休假排队系统，从而对通讯网络系统（离散时间排队系统）建立更切合实际的准确的模型.

［1］ 田乃硕，岳德权.拟生灭过程与矩阵几何解［M］.北京：科学出版社，2002.

［2］ 田乃硕.休假随机服务系统［M］.北京：北京大学出版社，2001.

［3］ Gelenbe E.Queues with Negative Arrivals［J］.J.of Applied Probability，1991，28（1）：245-250.

［4］ Peter G.Harrison，Edwige Piter.The M／G／1 Queue with Negative Customers［J］.Advances in Applied Probability，1996，32（2）：540-566.

［5］ 陈燕，朱翼隽，陈洋.一类具有负顾客的M／G／1休假排队模型［J］.兰州大学学报（自然科学版），2005，41（1）：118-121.

［6］ 杜贞斌，朱翼隽，肖江，陈洋.负顾客的M／G／1排队模型［J］.江苏大学学报（自然科学版），2002，23（3）：91-94.

［7］ Servi L D，Finn S G.M／M／1 queues with working vacations（M／M／1／WV）［J］.Performance Evaluation，2002，50（1）：41-52.

［8］ Liu Wen-yuan，Xu Xiu-li，Tian Nai-shuo.Stochastic decompositions in the M／M／1 queue with working vacations［J］.Operations Research Letters，2007，35（5）：595-600.

［9］ Yutakababa.Analysis of a GI／M／1 queue with multiple working vacations［J］.Operations Research Letters，2005，33（2）：201-209.

［10］ Keilson J，Servi L D.A distributional form of Little’s law［J］.Operations Research Letters，1988，7（5）：223-227.

M／M／1 Queuing System with RCE Strategy of Negative Customers and Working Vacation

GU Qing-feng
（Faculty of Science，Zhejiang Forestry College，Lin’an，Zhejiang 311300，China）

Consider an M／M／1 queue with vacations such that the server works with different rates rather than completely stops during a vacation period.In order to solve the interfering factors take place in the M／M／1 queuing system，the M／M／1 queuing system with negative customers and working vacations is studied.The serve rules are First Come First Served.The working vacation policy is exhaustive service and multiple working vacations.Negative customers remove positive customers only one by one at the tail（if present）.When a negative customer arrives，if the system is empty，it will disappear.Negative customers need no services.Using QBD（quasi birth and death）process and Matrix-Geometric solution，we gain the steady-state distributions for the number of customers in the system，point out the result of stochastic decomposition of the queue length and obtain mean of the system size of positive customers and waiting time.

negative customers；working vacations；matrix-geometric solution；steady-state distributions；stochastic decomposition

O226

B

1672-1454（2010）05-0125-06

2007-12-03