离散状态方程在人口预测问题中的应用

苑延华， 宋作忠， 姚 君

（黑龙江科技学院数力系，哈尔滨 150027）

离散状态方程在人口预测问题中的应用

苑延华， 宋作忠， 姚 君

（黑龙江科技学院数力系，哈尔滨 150027）

应用地域状态变量建立了人口发展的离散模型.一个重要目的就是评价中国的城市化和人口政策产生的影响.这些问题包括人口数量的预测和关于一些人口指标的讨论，如：人口地域分布、人口年龄分布、性别比、老龄化、抚养率，等.进而讨论了应在何时采取怎样的政策来应对未来的人口困境.

人口发展的离散模型；约束最小二乘估计；城镇化；老龄化

1 引 言

人是社会经济活动的主体，人口的发展变动趋势，对社会经济发展产生极大的影响，如资源分配、城市建设等，因此人口预测问题在社会经济发展实践中占有十分重要的地位.我国是一个人口大国，人口的增长一直是制约着我国发展的重要因素.特别是在实行计划生育政策的36年的时间里，我国人口增长得到了有效的控制，但是随着改革开放的不断深入，人口城镇化比例发生剧烈变化，对城市、镇、乡的经济发展产生了深远的影响.随着大量的农村劳动力向城镇转移，使得我国人口的城、镇、乡分布的分析和预测成为人们关心的重要问题之一.近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比偏高，人口抚养比的持续升高等因素，这些都影响着中国经济增长的进程与成果.

2 问题分析与模型假设

2.1 问题分析

通过对2001—2005年中国市、镇、乡人口数量及死亡率的年龄分布的统计研究，我们可以发现一些基本规律：

规律1 人口年龄分布的传动特性

也就是说，随着时间的发展，我国市、镇、乡里的同一性别人口比例按年龄的分布具有时间传动性.图1显示城市男性人口比例的年龄分布图，由此可知，1960年代的男性人口比例在2001至2005年一直处于比例峰值处，这说明当时的生育数量影响着这一时代人占总人口的比例数值，可见生育率影响着人口比例的年龄分布率，即人口年龄分布具有时间传动的特性.

规律2 死亡率年龄分布的稳定性

同一地域同一性别人的死亡率的年龄分布具有时间不变性.并且死亡率的分布呈现出J型，即婴儿段和高龄段的自然死亡率高，少年、青年、中年段的自然死亡率较低，显现出先降低后平稳发展最后快速升高的趋势.

规律3 生育率年龄分布具有地域稳定性

图1 2001—2005年城市男性占市总人口比例的年龄分布

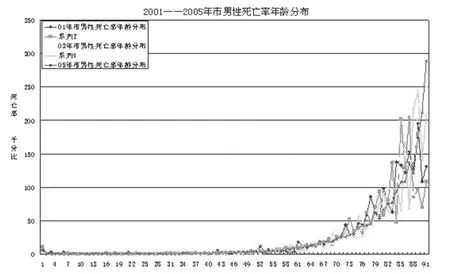
图2 城市男性死亡率的年龄分布图（2001—2005年）

图3 新生婴儿由k龄妇女生育的比率的年龄分布图

图3（a）是2001至2005年城市新生婴儿由k龄妇女生育的比率的年龄分布，由此可见这个生育率的稳定性，而图3（b）说明了新生婴儿由k龄妇女生育比率的年龄分布在地域之间的差别，而且可以发现按乡、镇、市育龄妇女生育年龄的主体向大龄发展的趋势，图中生育率是指m年里新生婴儿由k年龄段的妇女生育的概率.

图4表示k龄妇女千人生育率在不同地域之间的差异，我们可以发现三地妇女的生育率按乡、镇、市的顺序呈现出递减的态势，而且育龄妇女千人生育率为40‰以上的年龄区间有变短的趋势.

图4 市、镇、乡育龄妇女千人生育率的年龄分布

规律4 社会总生育率具有逐年递减性

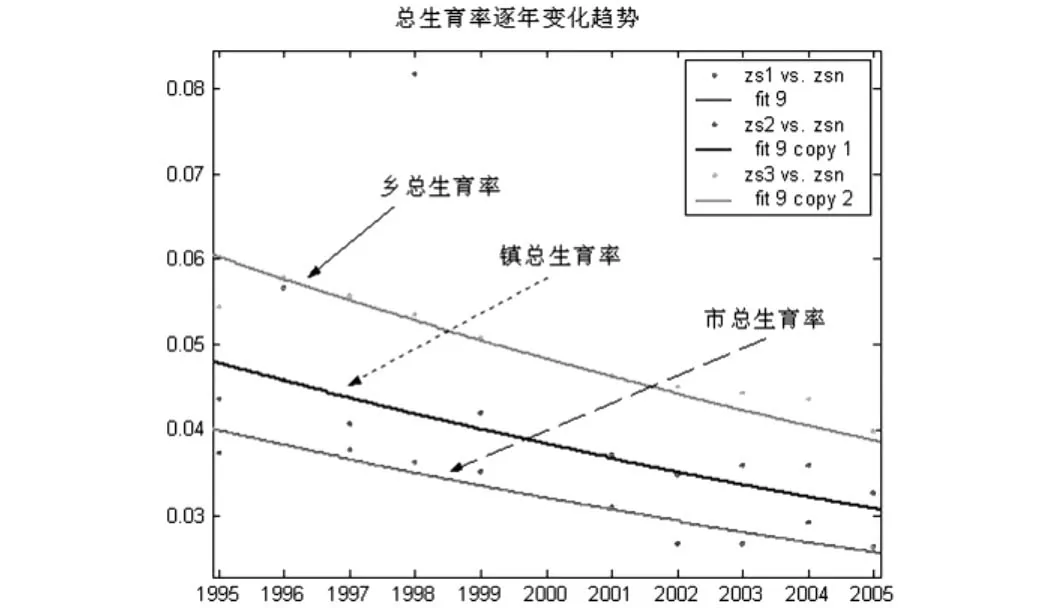
图5 市、镇、乡总生育率的统计图（1995—2005年）

由图5，可以发现1995年到2005年的统计数据显示出社会总生育率具有逐年下降的趋势，这和已有的研究成果“社会发展水平高，总生育水平低”的结果相一致.

2.2 模型假设

假设1：我国人口政策保持现状不变，不增加或减少关于人口迁移或生育有关的政策；

假设2：我国人口具有地域封闭性，即没有大规模的国际迁入与迁出；

假设3：我国人口按地缘分成城市人口、镇人口、乡人口三个基本类型；

假设4：每类人口的变化与迁入率、迁出率、死亡率有关；

假设5：新生人口数量只受育龄妇女的数量及其生育率的影响；

假设6：我国社会生育模式不变.

3 符号说明

记i表示地区，则当i＝1时表示城市，i＝2时表示镇，i＝3时表示乡；以j表示性别，则当j＝1时，表示男性，j＝2时，表示女性；k表示年龄，且k＝1，2，….于是为说明的方便引进以下记号：

xrij（k，m）：m年末i地区j性别k年龄段占i地总人口的比率；

dij（k，m）：m年末i地区j性别k年龄段人的死亡率，k＝0，1，2，…；

OTilj（k，m）：m年末i地区j性别k年龄段的人口迁往l地区的比率，且OTilj（k，m）≥0；

bij（0，m）：m年末i地区j性别婴儿总数；

pri2（k，m）：m年末i地区在k年龄段育龄妇女的千人生育率；

xti（m）：m年末i地区的总人口；xij（k，m）：m年末i地区j性别k年龄段的总人口，且

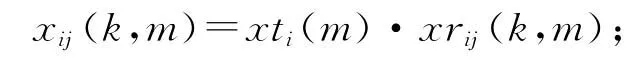
gri（m）：m年末i地区的新生儿中女孩的比例；

sij（k，m）：m年末i地区j性别k年龄段人口容量比；

πi（k）：i地区新生婴儿由k龄妇所生概率；

yi（m）：m年末i地总生育率.

4 模型建立与模型求解

4.1 基本模型

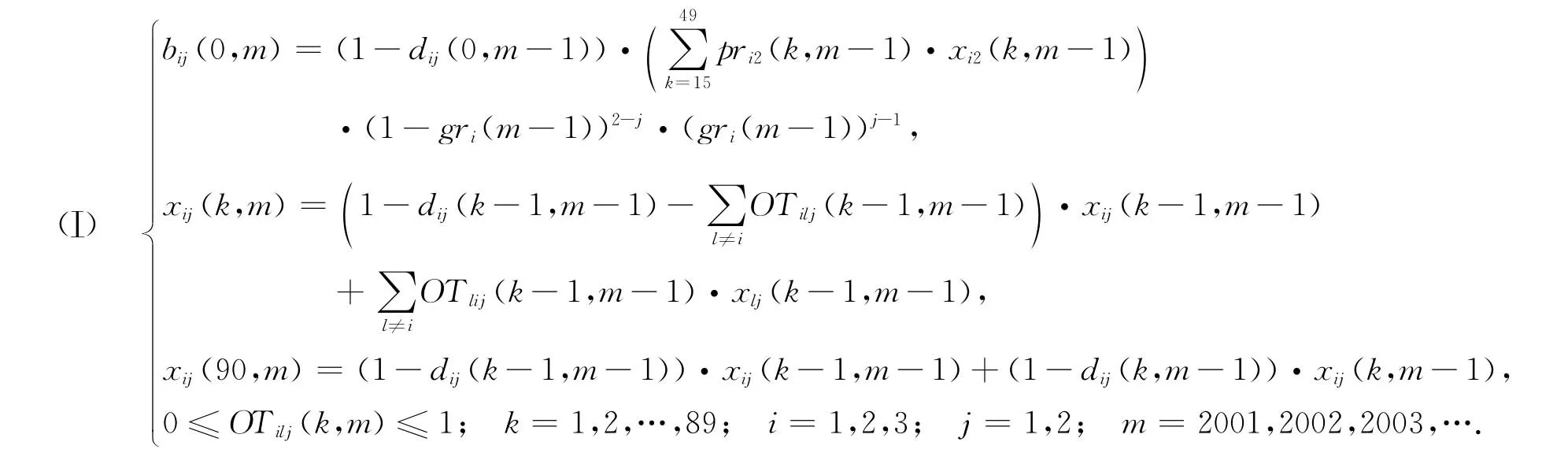
说明 上述离散模型（Ⅰ）是根据基本假设1—5建立起来的，其中bij（0，m）表示m年末i地区j性别新生婴儿人数，它与婴儿死亡率、性别比及育龄妇女生育率的年龄分布有关；xij（k，m）等于该地同性别前一年龄段人口的净剩余量加上外地人口迁入量，其中

迁出率与i地区j性别人口容量的剩余量成正比.

这个人口模型描述了我国境内人口地区间的流动规律，以及人口总量的发展规律，同时对人口性别特性也建立了动态描述.

4.2 简化模型

我们假设dij（k，m），OTilj（k，m），pri2（k，m），gri（m），sij（k，m）均不随时间m发生变化，于是离散模型（Ⅰ）简化为

4.3 参数估计方法及结果

由所给的统计量上看，目前我国新生婴儿性别比偏高，具有较严重的性别选择，根据假设6，我们按现在有性别选择倾向的生育模式进行预测，这里gri取i地区1995—2005新生婴儿性别比的平均值；死亡率dij（k）用2001—2005年所给数据的平均值作为估计值；生育率的年龄分布也用每种情况对应平均值进行估计.关于迁出率OTilj（k）的估计，由于目前我国正处在城镇化的过程之中，因而设仅有乡向市、镇的迁移，其余的迁移率均为零.应用约束最小二乘法进行估计，数学模型如下：

估计结果如图6所示，由此可见，乡村人口向城市迁移主要集中在青壮年龄段上，而向镇迁移的人口几乎每个年龄段的人都有.图7显示对于乡男子向城市迁移的估计在60岁之前拟合性较好，60岁之后拟合结果比较差.结合实际，我们假设乡里60岁以上人口（包括女子）不向城市、镇迁移，因为这部分人口即使迁向城市，也因不具备劳动能力而是受抚养的对象.

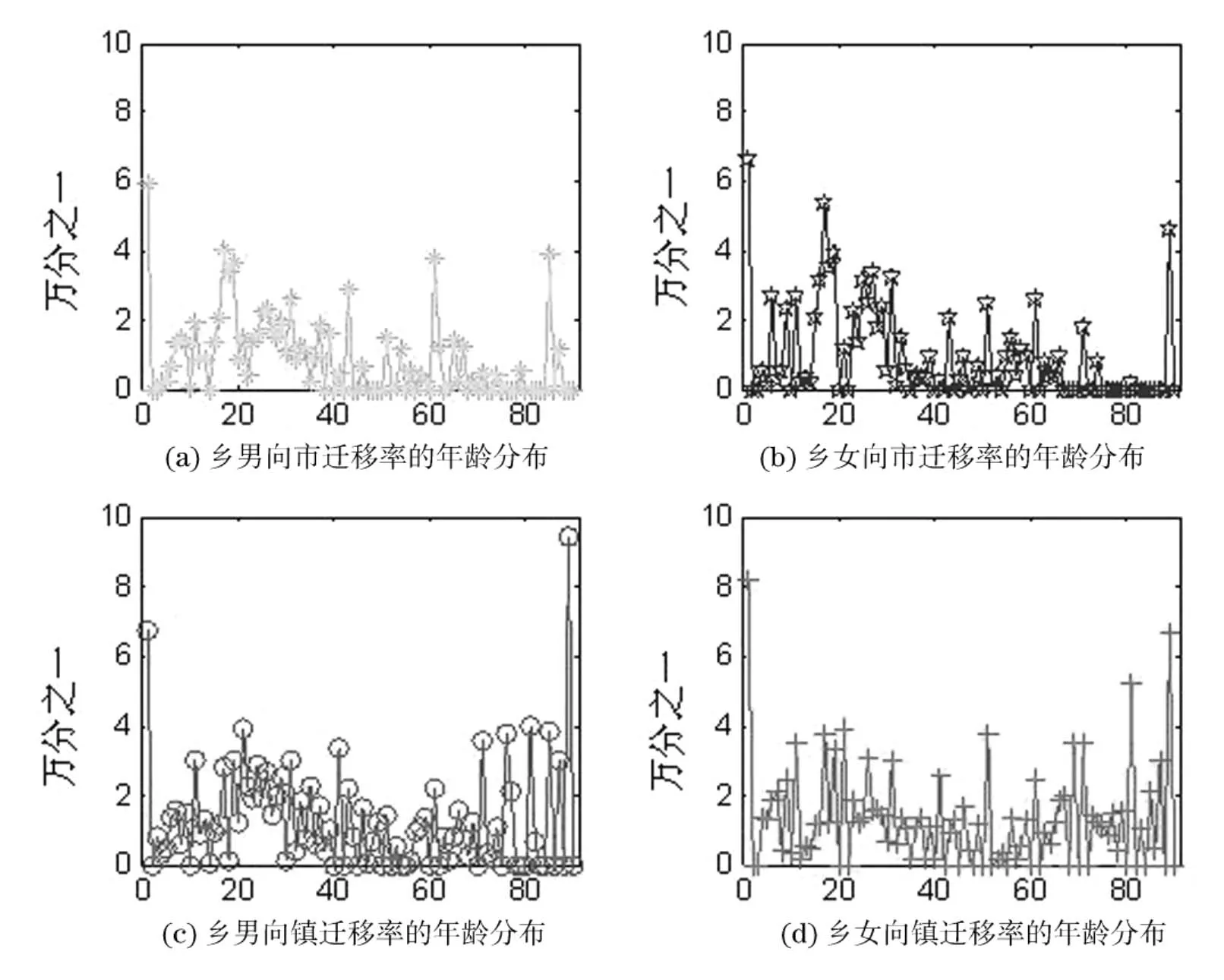
图6 乡男、女迁出率年龄分布（单位：万分之一）

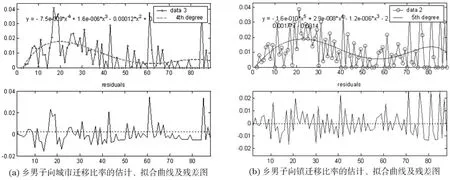
图7 乡男子向城市（a）、镇（b）迁移比率的估计、拟合曲线及拟合残差图

于是迁移率参数估计的改进模型为

4.4 模型预测及结果分析

4.4.1 误差分析

按上述方法进行参数估计后进行预测，我们以2001年的数据为初值，经计算可得人口数据的估计值（见表1），从观测值与估计值之间的对比可见本模型在人口总量的估计中预测数据值偏低，大约5年误差为600万人口，而且预测时间越长，误差越大，产生总人口误差的根源应该是妇女生育率及人口死亡率的估计误差.

表1 社会总人口的预测值与观察值的比较（单位：亿）

4.4.2 模型的预测结果

从模型（Ⅱ）的计算结果我们获得了社会总人口2001—2050年的预测结果及市、镇、乡人口分别在总人口中比例的预测结果（如图8），从我们这个预测结果上可以看到中国人口在2020年时将达到最大值13.44亿，此后人口总量具有下降的趋势.由人口地域分布的预测可见在2050年时，市、镇总人口数将达到社会总人口的80%.在2020至2030年间市、镇、乡人口比例持平.由图9（1-3）可见，中国社会未来人口老龄化趋于严重，社会抚养比加大，育龄人口中男性人口数量偏高.这些都预示着社会保障和经济建设部门要提前研究相应的制度设立，以保证整个社会的安定局面及人民生活的富庶.

图8 2001—2050年中国人口数量及状态结构预测

图9 2001—2050预测结果

此外，图10给出了若在2035年后调整生育政策为一家1.5个小孩，中国百年间人口发展的趋势预测，可以看到人口总量在2080年前压力不大，但2100年后的增长趋势也让我们深感忧虑.与此同时，2010年后社会总抚养比居高不下，这为提高社会发展水平，加快社会进步的步伐，提高人民生活水平的目标实现，提出了现实且难以逾越的障碍.不过，在这一政策下，2080年之后社会人口的年龄结构却是令人欢欣鼓舞的.

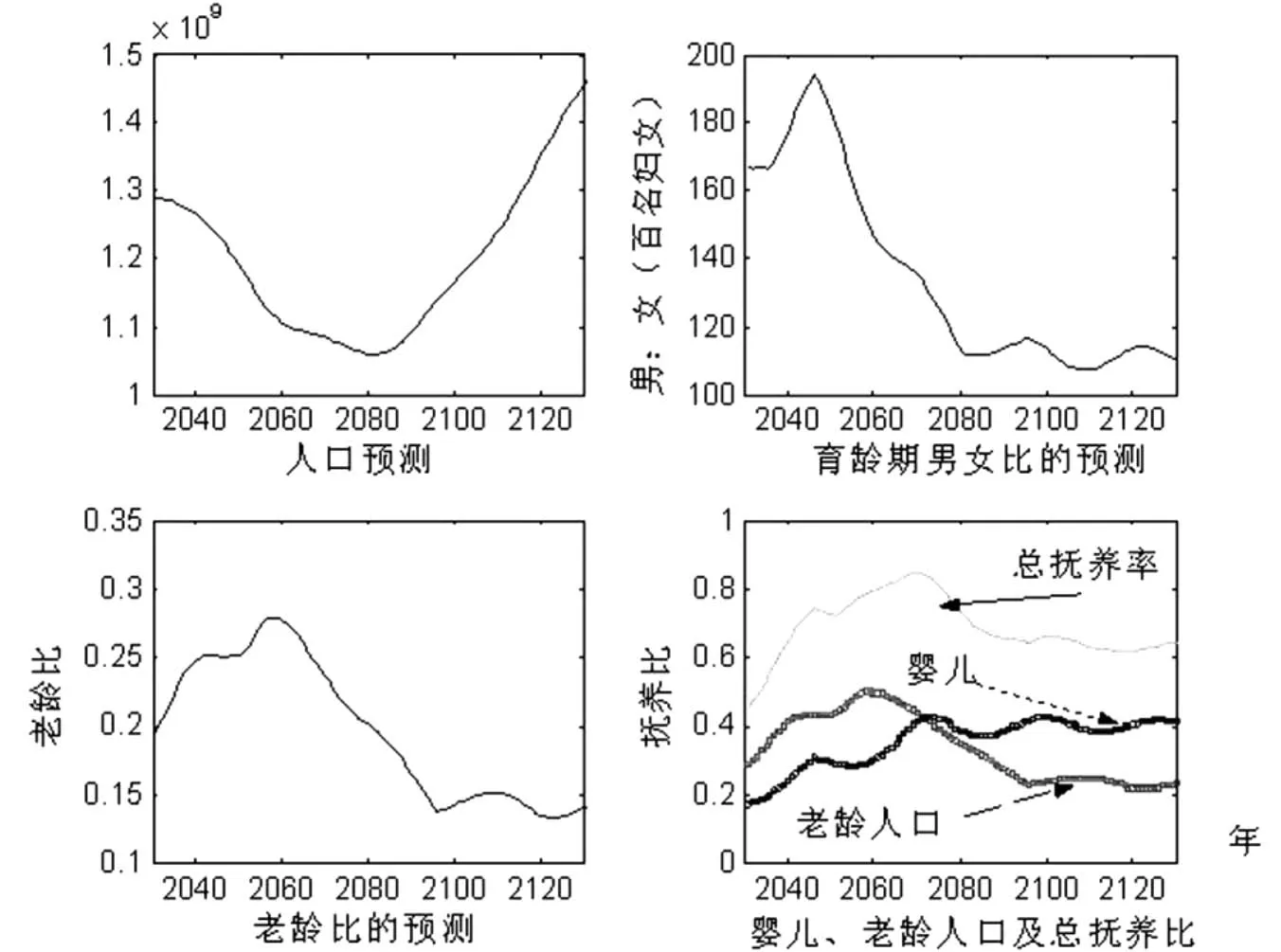
图10 中国社会人口组成的远期预测（调整生育政策后）

5 模型评价

本文通过引进人口地域状态变量，描述了改革开放以后人口流动的规律性，并在人口限制政策下预测了未来50年内中国人口总量、人口性别、社会劳动人口的总抚养率等重点问题.本模型的优点在于包含了人的生存地域特性，同时还引入社会发展后人们生育观的时变参数（育龄妇女的生育率），这保证了预测结果的可信度.虽然这个模型还无法包含随着社会人口地域结构的变迁、经济发展模式的改变，人们迁徙规律的改变、生育观念的改变等内容，但却可以为社会制度的规划、发展规划提供有益的参考.

［1］ 中华人民共和国国家统计局.中国统计年鉴［M］.北京：中国统计出版社，2003.

［2］ 门可佩，曾卫.中国未来50年人口发展预测研究［J］.数量经济技术经济研究，2004（3）：12-17.

［3］ 虞丽萍.人口年龄结构模型建模与预测［D］.北京：上海交通大学硕士学位论文，2007.

The Application of Discrete State Equation on Population Forecasting Problem

YUAN Yan-hua， SONG Zuo-zhong， YAO Jun
（Department of Math.and Mech.，Heilongjiang Institute of Science and Technology，Harbin 150027，China）

We establish a discrete model of population development by the use of geographical state variables.One of the important aims of this discrete model is to evaluate the influences of urbanization and population policy in China.These population problems include the population prediction and some discussions about population indexes，such as，the geographical distribution of population，the population age distribution，sex ratio，aging ratio，dependency ratio.Then，we discuss how to adopt appropriate policy for the future population plight in different stages.

a discrete model of population development；constrained least squares estimation；urbanization；the aging of population

C924.2

B

1672-1454（2010）05-0117-08

2008-02-27；

2008-05-28

黑龙江省教育厅科学技术研究项目（10551285）