非奇异H-矩阵的实用判定

兰 溪， 孙玉祥

（1.吉林油田第十一中学，吉林松原 138000； 2.北华大学师范学院数学系代数教研室，吉林 132013）

非奇异H-矩阵的实用判定

兰 溪1， 孙玉祥2

（1.吉林油田第十一中学，吉林松原 138000； 2.北华大学师范学院数学系代数教研室，吉林 132013）

H-矩阵在许多领域中都起着非常重要的作用，例如数学分析、矩阵理论、数学经济学、控制论等.但是在实际运用中判定H-矩阵却十分困难.本文类似于文［4］，均以α-对角占优理论为基础，给出H-矩阵的若干实用判定，改进了文［3］的相应结果.

非奇异H-矩阵；广义严格对角占优矩阵；广义严格α-对角占优矩阵

1 引言及记号

众所周知，广义严格对角占优矩阵就是非奇异H-矩阵.因非奇异H-矩阵主对角元素非零，所以本文假定所涉及矩阵主对角元非零，设A＝（aij）∈n×n为n阶复方阵，N＝｛1，2，…，n｝.设A的比较矩阵M（A）＝（mij）∈R Rn×n为n阶实方阵，其中

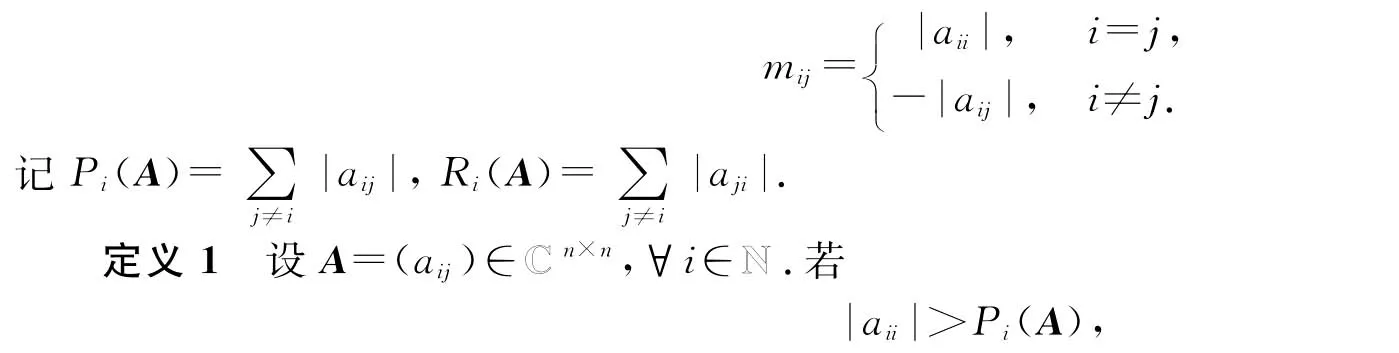
则称为严格对角占优矩阵，记为A∈D.若存在一组正数di（i＝1，2，…，n），使得

则称A为广义严格对角占优矩阵，记为A∈H.

定义2 设A＝（aij）∈n×n，若存在α∈（0，1），使∀i∈N N，有

则称A为严格α-对角占优矩阵，记A∈D（α）.若存在一组正数di（i＝1，2，…，n），使

则称A为广义严格α-对角占优矩阵，记为A∈D＊（α）.

引理1［1］设A＝（aij）∈n×n，则A是广义严格对角占优矩阵当且仅当A是广义严格α-对角占优矩阵.

引理2［2］设A＝（aij）∈n×n，B＝M（A）＋MT（A）.若B是广义严格对角占优矩阵，则A是广义严格对角占优矩阵.

2 主要结论

定理设A＝（aij）∈C Cn×n.若存在α∈（0，1），使

则B为广义严格α-对角占优矩阵，由引理1知B为广义严格对角占优矩阵，再由引理2知A∈H.

3 数值例子

有了上述定理我们就很容易判定高阶矩阵是否为非奇异H-矩阵.看下面的例子：

［1］ Sun Yu-Xiang.An improvement on a theorem by Ostrowski and its applications［J］.North-eastern Math，1991，7（4）：497-502.

［2］ Berman A and Plemmons R J.Nonnegative matrices in the mathematical sciences［M］.New York：Academic，1979.

［3］ 徐仲，陆全.判定广义严格对角占优矩阵的一组充分条件［J］.工程数学学报，2001，18（3）：11-15.

［4］ 谢清明.判定广义对角占优矩阵的几个充分条件［J］.工程数学学报，2006，23（4）：757-760.

Practical Criterion for Nonsingular H-Matrices

LAN Xi1， SUN Yu-xiang2
（1.No.11 Senior Middle School of Jilin Oil Field，Songyuan，Jilin 138000，China；
2.Department of Mathematics，Normal Science College，Beihua University，Jilin 132013，China）

H-matrices play a very important role in many fields like Numerical Analysis，Matrix theory，Mathematical Economics，Control theory，etc.But it is difficult to judge H-matrices in practice.In this paper，we give some practical criterions for nonsingular H-matrices abase on the theory ofα-diagonally dominant matrices，it is similar to［4］.And improve the results of［3］.

nonsingular H-matrices；generalized strictly diagonally dominant matrix；generalized strictlyα-diagonally dominant matrix

O151.21

A

1672-1454（2010）05-0109-03

2008-06-16