基于细胞自动机演化算法求解无约束函数优化问题

曾志峰

(湖南人文科技学院通信与控制工程系,湖南娄底 417001)

基于细胞自动机演化算法求解无约束函数优化问题

曾志峰

(湖南人文科技学院通信与控制工程系,湖南娄底 417001)

在最优化领域目前广泛应用的智能优化算法有遗传算法、模拟退火算法、神经网络算法等。但这些算法的实现模式都还是基于串行模式。利用细胞自动机来解决优化问题,也就意味着能够建立极度并行的解决最优化问题的程序。提出了一种基于细胞自动机的演化算法,以求解无约束函数优化问题,并用实验分析了此算法的性能。

细胞自动机;函数优化;演化算法

细胞自动机是当前计算机科学的一个研究热点。细胞自动机本质上是一个时间离散化、空间离散化的动力学系统。它所具有的极度并行性、基本单元的简单性、细胞相互作用的局部性等特点引起众多学科的学者们越来越多的关注。

在最优化领域,不断出现一些超大规模的非线性问题,由于这些问题的复杂性、强约束性、非线性、不确定性,使得这类问题难于解答,而且当前这类问题一般使用的很多算法的架构依然是建立在 Von Neumann结构的计算机系统上,不太适合细胞架构的机器。假如我们利用细胞自动机来解决优化问题,也就意味着能够建立极度并行的解决最优化问题的程序。另外,在函数优化方面,生活中许多问题用传统的数学计算方法来求精确解是不可能的,实际应用中只要求求出其“优化解”即可。演化计算求解无约束函数优化问题,实际上是对函数参数 (自变量)不断优化的过程。

1 无约束最优化问题

无约束最优化问题的一般模型为:

其中 Rn为 n维欧式空间,f(x):Rn→R为连续可微函数[1]。

求解无约束最优化问题的算法主要是迭代算法,常采用如下形式:

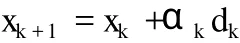
其中αk是通过某种线性搜索而获得的步长,dk为某一下降方向,对αk和 dk的不同选择就构成了不同的迭代算法。广泛采用的最优化计算方法有 N ew ton型方法、最速下降方法、共轭梯度方法、信赖域方法以及内点算法等等。N ew ton型方法和信赖域方法对中小型最优化问题具有较好的收敛特征,但它在每步迭代时需要的存贮量和计算工作量较大,不适于求解大型最优化问题;最速下降算法在每步迭代时需要的存贮量和计算工作量较小,可用于求解大型最优化问题,但该算法的收敛速度慢且容易在最优点附近产生拉锯现象。

De Jong F2函数[2]是一个典型的无约束最优化问题,由于该问题在早期下降速度最快的地方后期下降速度很慢,所以一般的算法并不容易找到最优解,标准的精英演化算法对这个问题常常很慢收敛到最优解。其函数表达式为:

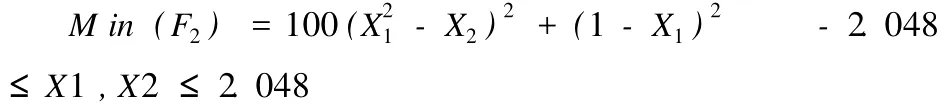
其图形如图 1所示。该函数的最小值为 0,位于 (1,1)。

图1 De Jong F2函数的图象

2 基于细胞自动机演化算法

2.1 算法有关定义

一个演化细胞自动机 (Evolutionary Cellular Automata)ECA=[3]

(1)U为状态空间集合,UEi为第 i个细胞所取的状态,其中,U={x1,x2,…,xn}∈X,即 U在向量空间 X中取值

(2)E为细胞集合,Ei为编号为 i的细胞

(3)N为邻居集合,Ni={Ej|Ej与 Ei的空间距离小于等于常数 r}

(4)T为离散时间

(5)F为转换函数集合 (也称为转换规则表),第 i细胞的转换函数 Fi满足 Fi:Uni×T→U,其中,Fi为演化算子中的交叉和变异算子若要将细胞自动机用于优化,显然需要对它改造。

构造 ECA满足如下条件:

(1)令 E0是所有细胞元的邻居

其中 r为常数,g为最小化函数,UEi为细胞 i的当前状态,U′由 UNi状态使用某一种规则 (算子)产生。如果算子选用得当,则该细胞自动机可用于优化函数 g,使 g以概率1收敛于全局极小值。

对于该算法,最主要的问题是 U’的生成,即 U’的生成规则,称之为细胞元的协同演化规则。可以选用的算子包括经典算法中的算子如最速下降,也可以选用模拟退火算子,也可以选用遗传算法中的杂交算子和变异算子,当然,也可以选用它们的组合。

若选用模拟退火算子或变异算子,则规则 3中的第三点可以略去。

2.2 算法描述

对于细胞元的协同演化规则,可以使用杂交算子和变异算子及它们的组合。如在一维细胞自动机中,对于函数优化问题,可以有:

(1)U′=t＊UE(I)+(1-t)＊UE(I+1) t为随机数

t为随机数

当然,还可以列出其他各种各样的协同演化规则。

在组合优化中,同样可以有很多种协同演化规则。如类似于 SGA的交叉算子,2-交叉法、k-交叉法、贪婪变异等。

实际上,在应用的过程中,算法没有必要一定收敛到全局最优,只需要求得满意解就可以了。在很多情况下,收敛到全局最优的代价是等同于枚举的。所以,使用下面的算法就可以达到较好的优化效果了。

也可以在其中加入随机变异算子,此时,算法为:

3 实验分析

简单遗传算法[4](SGA,simple GA)中采用的线性适应度以及恒定交叉、变异概率,容易造成算法早熟或停滞,且运行效率低。为此,国内、外诸多学者对简单遗传算法进行改进,如 Goldberg引入的线性拉伸方法 (LGA,linear GA)以及 Paul等提出的模拟退火思想,改进了 SGA中的线性适应度;针对恒定交叉、变异概率引起的不足,Srinvivas等提出自适应交叉、变异概率,马钧水等采用大变异操作代替 SGA中恒定概率的变异操作[5]。

本文也用 SGA算法求解该函数,算法采用轮盘赌选择策略,均匀杂交,随机变异,发现该算法有很多缺点:

1)评价函数的选取需要相当多的经验,若选取不当,有收敛到局部极大值的可能性大大增加。

2)精度相对于本算法比较差,一般为 10-5-10-6(本算法为 10-9-10-10)。

3)理论上是总可以收敛到全局最优解的,实际上常常不可能,因为算法常常需要在有限步内终止。

在实验中,利用 SGA计算了 10次,种群大小 100,交叉概率选为 0.9,变异概率为 0.1,终止条件为计算 1000代,计算结果的精度为 10-5。

实验的结果如表1:

表1 SGA与本算法的比较

从以上实验数据中,可以看到本算法具有较好的性能。

4 结论

最优化问题在实际工程中常见,各种最优化方法应运而生,人们也提出了各种各样的函数来检测最优化算法的性能。本文提到的算法具有较好的性能,但是,遗憾的是,所有的算法,无论你采用什么算子,如果你提升对某一类问题的性能,那么该算法针对另外的某一类问题性能必然下降。

[1]SARKAR P.A brief history of cellular automata[J].ACM Computing Surveys,2000,32(1):45-49.

[2]BERLECAMP E R,CONWAY J H,GUY R K.W inning ways[J].Houston:Academic Press,1985,2(1):22-29.

[3]BURKSA W.Essayson cellular automata[J].Paris:Universityof Illinois Press,1972:56-98.

[4]WOLFRAM S.Cellular automaton on supercomputing,high-speed computing[J].Scientific Applications and Algorithm Design,1988:33-93.

[5]WOLFRAM S.Statistical mechanics of cellular automata[J].Reviews ofModem Physics,1983:68-69.

(责任编校:光明)

Opt im ization Problems about Answering Unconstra ined Function Based on Cellular Automata Evolution

ZENG Zhi-feng

(Depar tment of Communication and Control Engineering,Hunan Institute of Humanities,Science and Technology,Loudi,417001,China)

In the field of optimization,intelligentoptimization algorithms arewidely used,including genetic algorithm,simulated annealing and neutral network and so on.But implementation patterns of these algorithms are based on serial mode.When the cellular automation is applied to solve the problem of opt imization,itmeans thatwe can establish a program which can solve those problemswith super concurrency.An evolutionary algorithm based on the cellular automaton is raised to ans wer the optimization problem of unconstrained function.We also use the experiment to analyze the function of this algorithm.

cellular automata;function optimization;evolutionary algorithm

O242.1

A

1673-0712(2010)02-0027-03

2010-02-20.

曾志峰 (1976- ),男,湖南双峰人,湖南人文科技学院通信与控制工程系讲师,研究方向:数据挖掘,计算机网络。