高校教师整体素质的多元联系数评价方法

涂晓杰

(湖南人文科技学院数学与应用数学系,湖南娄底 417001)

高校教师整体素质的多元联系数评价方法

涂晓杰

(湖南人文科技学院数学与应用数学系,湖南娄底 417001)

用多元联系数评价法对高校教师的整体素质进行综合评价,实例表明此法客观、合理,简便易操作,具有一定的推广和实用价值。

多元联系数;教师整体素质;综合评价

对高校教师的整体素质进行综合评价,是教育管理的一个重要内容。目前,采用的评价方法大致有两类[1]:一类是传统的定性评价;一类是定性与定量相结合的评价。定性评价是指用“优、良、中、差”等类似的模糊语言对教师素质作出的评价,这种评价弹性大,不能客观合理地反映教师的真实情况。定量评价则是通过量化分析,来反映教师的素质情况,这种方法比较客观,是综合评价的发展趋势之一。现在已有多种定量评价方法被引入,比如模糊数学法、秩和比法、加权 TOPSIS法、层次分析法、灰色关联分析法等等。本文引入一种新的综合评价方法——多元联系数评价法,它不仅可以客观地反映教师素质的真实情况,而且能使定性描述定量化,可操作性强。

1 多元联系数[2]

多元联系数是同异反联系数

在 B i上的一种推广,其一般形式为:

(A,B1,B2,…,Bn,C均为非负实数)。当 n=2时,为 4元联系数

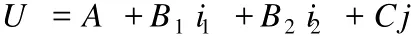
当 n=3时,为 5元联系数

……,等等。有时为了应用方便,多元联系数也写成下面的形式:

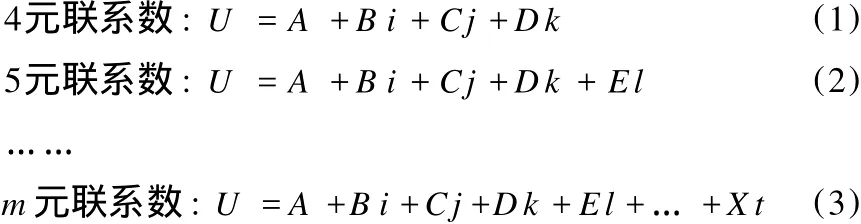
一般地,称多元联系数中的 A,B,C,D,E,…,X为联系分量,而 i,j,k,l,…,t为联系分量系数,通常 m(m=n+2)元联系数中最后一个联系分量系数恒为 -1,以与同异反联系数的 j=-1相对应,但在这之前的 m-2个联系分量系数 i,j,k,…的取值范围随着 m的增大而减小,如 4元联系数 (1)中的 k=-1,在均分取值原则下,i∈[0,1],j∈[-1,0];5元联系数 (2)中 l=-1,i∈[0.333,1],j∈[-0.333,0.333],k∈[-1,-0.333];……等等。多元联系数中,各联系分量系数在所属区间内取何值,视具体情况来定。比如,要保证最后结果更可靠,可从“最坏”角度对各联系分量系数取值[3],则在 4元联系数 (1)中,取 i=0,j=-1;在 5元联系数 (2)中,取 i=0.333,j=-0.333,k=-1。若将各联系分量系数所在区间的中位值作为该联系分量系数的值,则在 4元联系数 (1)中,i=0.5,j=-0.5;在 5元联系数 (2)中,i=0.667,j=0,k=-0.667。

如果在多元联系数 (3)中令 N=A+B+C+…+X,则得归一化后的多元联系数

2 多元联系数评价方法

2.1 确定评价人对某教师综合素质的每个指标中各指标的评价结果的联系数及多元联系数评价决策矩阵

设教师的综合素质有 m个指标 X1,X2,…,Xm,其中每个指标 Xp又分为 np个指标 xp1,xp2,…,xpnp(p=1,2,…,m),Xp中各指标的权重系数为 αp1,αp2,…,αpnp,这里

评为 Y1级的有人,评为 Y2级的有人 , … ,评为Ys级的有

则对 xpq(q=1,2,…,np)的评价结果的 s元联系数为:

归一化后的联系数为:

于是,得指标 Xp的多元联系数评价决策矩阵为:

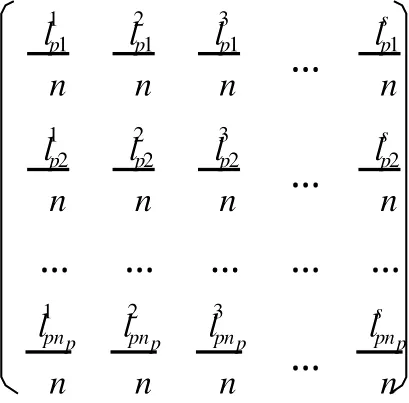
其中 p=1,2,…,m。

2.2 求出 n个评价人对指标 Xp(p=1,2,…,m)的评价结果的联系数μp(p=1,2,…,m)

2.3 计算 n个评价人对该教师综合素质的评价结果的联系数

设指标X1,X2,…,Xm的权重系数分别为,用(μ1,μ2,…,μm)T作为多元联系数评价决策矩阵,则该教师综合素质评价结果的 s元联系为:

2.4 在均分取值原则下,确定各联系分量系数 i,j,…,r的值并代入 (4)式,得联系数μ的值

2.5 由均分取值原则,确定等级 Y1,Y2,…,Ys所在取值范围,从而确定该教师综合素质所属等级

3 应用举例 (采用王娟[4]所给实例)

评价高校教师的综合素质有 4个指标:政治素质 X1,思想素质 X2,业务素质 X3,身体素质 X4。X1中又有 3个指标:政治立场 x11,政治观点 x12,政治品质 x13;X2中有 4个指标:人生观 x21,精神面貌 x22,思想方法 x23,思想品德x24;X3中有 4个指标:知识能力 x31,动手能力 x32,教学能力 x33,科研能力 x34;X4中有 3个指标:健康状况 x41,体力状况 x42,智力状况 x43。设评价结果分为五个等级:优秀(Y1)、良好 (Y2)、中等 (Y3)、及格 (Y4)、差 (Y5)。又设 12人专家评审组对各指标给出合理的权重系数,并对某教师的综合素质给予评定,其结果如下:

对某教师的专家评审

第一步:确定 x11,x12,x13的评价结果联系数 (也是归一化后的联系数)

由此得 X1的多元联系数评价决策矩阵为:

同理,X2,X3,X4的多元联系数评价决策矩阵分别为:

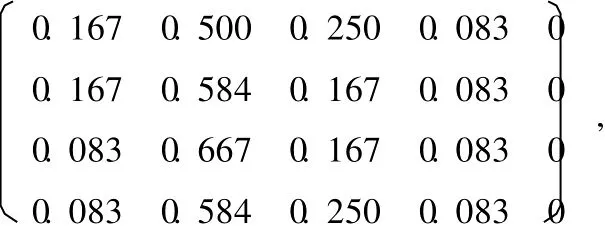
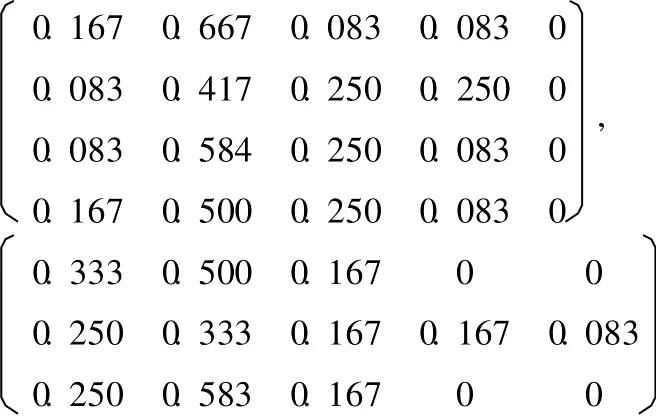
第二步:计算 12人专家评审组对 X1,X2,X3,X4的评价结果联系数

同理,

第三步:求出 12人专家组对该教师综合素质评价结果的联系数

第四步:μ为 5元联系数,l=-1,由均分取值原则,得

现约定各联系分量的系数在各自所属区间取区间中位值,则

由此得联系数μ的值:

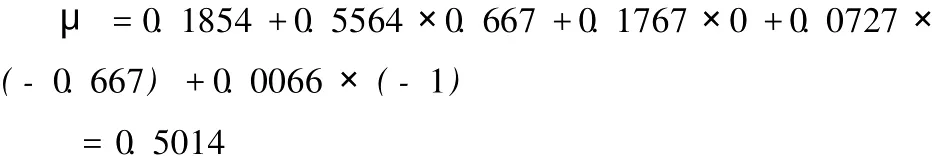
第五步:因归一化联系数μ的取值范围只能是区间 [-1,1],由均分取值原则得区间 [-1,-0.6],[-0.6,-0.2],[-0.2,0.2],[0.2,0.6],[0.6,1]分别对应于“差”、“及格 ”、“中等 ”、“良好 ”、“优秀 ”五个等级。故知 ,该教师综合素质属于“良好”,此结果与文[4]一致。

4 结语

多元联系数评价法客观、合理,简便易操作,可应用于多种领域的综合评价问题,前景比较看好。

[1]张玮,朱金福,赵成果.灰色关联分析法在教师评价模型中的应用[J].产业与科技论坛,2007,6(1):126-128.

[2]覃杰,赵克勤.多元联系数在医院医疗质量综合评价排序中的应用[J].中国医院统计,2004,11(3):195-196.

[3]吴亭.五元联系数在学生成绩发展趋势分析中的应用[J].数学的实践与认识,2009,39(5):53-59.

[4]王娟.高校教师考评的 Fuzzy方法 [J].长春师范学院学报,2003,22(1):86-88.

(责任编校:光明)

Muti-Crrelate Evaluation Methods about Colleges and Universities Teacher’sOverall Quality

TU Xiao-jie

(Depar tment ofMaths and ApplicationMaths,Hunan Institute of Humanities,Science and Teachnology,Loudi,417001,China)

Usingmulti-correlate evaluation methods,colleges and universities teachers’overall quallties are evaluated comprehesively.The method is objective,reasonable and easy to operate,which has certain popularization and pracical value.

multi-correlate;colleges and universities teacher;overall quality;evaluation

G645

A

1673-0712(2010)02-0007-03

2010-01-15.

涂晓杰 (1960-),女,湖南桃江人,湖南人文科技学院数学与应用数学系副教授,研究方向:基础数学、集对分析。