一个偶数表示为两个奇数之和的证明

陆毅

（江苏省连云港市东海县房山高级中学，江苏东海222341）

一个偶数表示为两个奇数之和的证明

陆毅

（江苏省连云港市东海县房山高级中学，江苏东海222341）

一个偶数表示为两个奇数之和有6种表达式，并且这6种表达式之间有一定的内在联系；用数学归纳法证明了这些表达式之间的联系.

奇数表达式；素数表达式；合数表达式；表达式的个数

0 引言

数论是许多学者研究的领域[1-4].我于2007年8月在美国《自然科学研究》上发表了题为《在偶数性质中发现一个有趣的问题》[5]的论文，东北师范大学的盛中平老师、苏州大学的张星晨、朱东亚老师、华东师范大学的许广龙博士、俄亥俄州大学数论博士陆三等老师都给予了高度评价，同时他们建议我有必要对该论文推导出的公式p=m+L或p=m+L+1及n=L+2m+t+2给予进一步证明［其中，p表示当偶数2n表为素数+素数与素数+合数或素数+1时的表达式个数，L表示当偶数2n表为两个素数之和时的表达式个数，n表示当偶数2n表为两个奇数之和时的表达式个数，2m表示当偶数2n表为素数+合数与合数+素数时的表达式个数，t表示当偶数2n表为两个合数之和时的表达式个数，2表示两个表达式：一个表达式是偶数2n表示为1与（2n-1）之和，另一个表达式是偶数2n表示为（2n-1）与1之和］.假如能够证出公式L＞0（即L=n-2m-t-2＞0），其意义更大.但我一直认为此公式已经推导出来了，没有必要去证明L＞0，因为证明L＞0是一件很容易的事情，只要精通数学的人都能证明.但他们一致认为，证明L＞0不是一件很容易的事情，并且建议我最好能给出证明.

经过5个月的思考，我终于找到证明L＞0的方法，并于2008年12月发表了题为《对“任何一个大于4的偶数都可以表示为两个奇数之和”的思考》[6]的论文.发表不久，南京师范大学数论专家陈永高老师、上海华东师范大学数论专家韩士安老师、首都师范大学数论专家王永辉老师均提出：证明L＞0的方法是对的，但证明过程还是存在问题，必须重新修改，否则不能说明证明L＞0是一件很容易的事情.

在众位数论专家的建议下，我经过几个月的思考，终于找到一种证明L＞0完整、简单而又详细的证明过程，但这个证明过程只是我个人认为是简单的，也许其他人还有更简单的方法.

1 说明

在推导公式之前首先补充说明一下，在文献［5-6］中提到的公式：p=m+L或p=m+L+1及n=L+2m+t+2，它们之间只是为了研究方便而进行的恒等变换.

在证明L＞0之前再简单叙述一下公式p=m+L或p=m+L+1及L=n-2m-t-2的推导过程[6].设任何一个大于4的偶数为2n（n＞2，n∈N，以下相同不再重述），显然，在偶数2n前面有n个是奇数，在这些奇数中假设有p个是素数（显然，p中不包括素数2，因为2是偶数而不是奇数），有q个是合数（显然，因为偶数8的前面没有合数，所以q可以等于0），因为1既不是素数也不是合数，于是n=p+q+1.因为任何一个大于4的偶数2n都可以用它前面的每一个奇数与它前面的一个特定的奇数之和来表示，其表达式的个数是n，即偶数2n=奇数+奇数；又因为奇数还可以分为素数、合数、1，所以按照这样的排列，偶数2n=奇数+奇数也只能有6种表达形式；当2n为小偶数时，2n表示为两个奇数之和的表达形式可能是6种表达形式中的某几种表达形式；当2n为充分大的偶数时，2n表示为两个奇数之和的表达形式中一定都含有6种表达形式.这6种表达形式为：①偶数2n可能表示为1与素数之和，即偶数2n=1+素数（或偶数2n也可能表示为1与合数之和，即偶数2n=1+合数）；②偶数2n还可能表示为素数与合数之和，即偶数2n=素数+合数；③偶数2n还可能表示为两个素数之和，即偶数2n=素数+素数；④偶数2n还可能表示为两个合数之和，即偶数2n=合数+合数；⑤偶数2n还可能表示为合数与素数之和，即偶数2n=合数+素数；⑥偶数2n还可能表示为素数与1之和，即偶数2n=素数+1（或偶数2n也可能表示为合数与1之和，即偶数2n=合数+1）.

因为偶数2n可以用它前面的每一个奇数与它前面的一个特定的奇数之和来表示，其表达式个数为n；又因为在偶数2n前面有n个是奇数，在n个奇数中含有p个是素数，所以在n个奇数表达式（偶数2n表示为两个奇数之和的表达形式称为奇数表达式）中含有p个是素数表达式（偶数2n表示为一个素数与一个特定奇数之和的表达形式称素数表达式）；在p个素数表达式中，每一个素数表达式必定有一个素数跟一个特定奇数之和，其形式也一定是下列3种表达形式中的一种：①偶数2n可能表示为素数与合数之和，即偶数2n=素数+合数；②偶数2n还可能表示为两个素数之和，即偶数2n=素数+素数；③偶数2n还可能表示为素数与1之和，即偶数2n=素数+1.现在假设在p个素数表达式中含有L个素数表达式是两个素数之和的表达形式，同时还假设在p个素数表达式中含有m个素数表达式是素数与合数之和的表达形式，如果2n-1是素数，那么在p个素数表达式中一定含有“偶数2n表示为素数与1之和”这个表达式，即2n=（2n-1）+1，因此，p=m+L+1；如果2n-1不是素数，那么在p个素数表达式中一定没有“偶数2n表示为素数与1之和”这个表达式，因此，p=m+L.

同样可以得到，在n个奇数表达式中含有q个是合数表达式（偶数2n表示为一个合数与一个特定奇数之和的表达形式称为合数表达式）.显然，n=p+q+1，在这里n表示当偶数2n表为奇数表达式时的表达式个数，p表示当偶数2n表为素数表达式时的表达式个数，q表示当偶数2n表为合数表达式时的表达式个数，1表示当偶数2n表示为1与（2n-1）之和时的表达式个数.例如，当偶数2n=24时，偶数24表示为奇数表达式时的表达式个数是12，即n=12，具体如下：24=1+23=3+21=5+19=7+17=9+15=11+13=13+11=15+9=17+7=19+5=21+3=23+1.偶数24表示为素数表达式时的表达式个数是8，即p=8，具体如下：24=3+21=5+19=7+17=11+13=13+11=17+7=19+5=23+1.偶数24表示为合数表达式时的表达式个数是3，即q=3，具体如下：24=9+15=15+9=21+3.偶数24表示为1+23时的表达式个数是1.在q个合数表达式中，每一个合数表达式必定含有一个合数与一个特定奇数之和，其表达式的形式也一定是下列3种表达式中的一种：①偶数2n可能表示为两个合数之和，即偶数2n=合数+合数；②偶数2n还可能表示为合数与素数之和，即偶数2n=合数+素数；③偶数2n还可能表示为合数与1之和，即偶数2n=合数+1.同样可以假设在q个合数表达式中含有t个合数表达式是两个合数之和的表达形式.显然，在q个合数表达式中也含有m个合数表达式是合数与素数之和的表达形式（因为素数+合数表示素数表达式与合数+素数表示合数表达式，只是顺序和名称不一样，其实质是一样的，因此有m个是素数+合数的素数表达式，同样也就有m个是合数+素数的合数表达式.例如，12=3+9=9+3，其中3+9是表示一个素数表达式，是素数与合数之和的表达形式；9+3是表示一个合数表达式，是合数与素数之和的表达形式）.如果2n-1是合数，那么在q个合数表达式中一定含有“偶数2n表示为合数与1之和”这个表达式，即2n=（2n-1）+1，因此，q=m+t+1；如果2n-1不是合数，当然在q个合数表达式中一定没有“偶数2n表示为合数与1之和”这个表达式，因此，q=m+t.

因为p=m+L或p=m+L+1，q=m+t或q=m+t+1，又因为2n-1要么是一个素数，要么是一个合数，只能是其中的一种（注意，2n-1＞1），所以，n=p+q+1=m+t+m+L+2，即n=L+2m+t+2，它又可以变形为L=n-2m-t-2，其中，n表示当偶数2n表为两个奇数之和时的表达式个数，L表示当偶数2n表为两个素数之和时的表达式个数，2m表示当偶数2n表为素数+合数与合数+素数时的表达式个数，t表示当偶数2n表为两个合数之和时的表达式个数，2表示两个表达式，一个表达式是偶数2n表示为1与（2n-1）之和，另一个表达式是偶数2n表示为（2n-1）与1之和.

我们再简单说一下证明L＞0的原因，因为在数学中经常碰到很多个偶数不仅可以表示为两个素数之和，而且它们表示为两个素数之和的表达式个数并不唯一.例如，10=3+7=5+5，14=3+11=7+7，16=3+13=5+11，18=5+13=7+11，20=3+17=7+13，22=3+19=5+17=11+11，24=5+19=7+17=11+13，26=3+23=7+19=13+13，28=5+23=11+17，30=7+23=11+19=13+17，32=3+29=13+19，34=3+31=5+29=11+23=17+17，36=5+31=7+29=13+23=17+19，38=7+31=19+19，40=3+37=11+29=17+23，…….这些例子在数学中是比较简单、常见的，却一直没有引起人们的关注和思考.往往简单的问题都隐藏着绝妙的玄机.上面的那些例子暗示我们去思考：一个大于4的偶数2n表示为两个素数之和的表达式个数到底有多少，跟什么有关？像这样的偶数有多少，又有什么规律？如何去寻找？是不是每一个大于4的偶数2n都可以表示为两个素数之和呢？我按照这个思路，先从偶数6开始寻找，一直到偶数6 002，书写了几百万个数学式子，终于发现：偶数2n表示为两个素数之和的表达式个数，随着该偶数2n的增大而成波动性增加，即L值在增加过程中有少数是相对降低的，但总的趋势是增加的.这个结论只是从一部分事例中获得，而哥德巴赫猜想只是它（L=n-2m-t-2）的一部分，想利用这个结论为哥德巴赫猜想的研究开辟新的途径，就必须从理论上证明L＞0.我们现在根据公式L=p-m或L=p-m-1（即L=n-2m-t-2），再从理论上来研究：在n个奇数表达式中含有两个素数之和的表达式个数L.

2 证明过程

根据题意，L只能是非负整数，只要证明L＞0，就可以充分说明：每一个大于4的偶数2n都可以表示为两个奇素数之和，而证明公式L=p-m或L=p-m-1，利用数学归纳法即可证出，具体证明过程如下.

当m=0时：

当偶数2n=4时，4表示为两个奇数之和的表达式有2个，即4=1+3=3+1，4不能表示为素数+合数的表达形式，则p=m+L+1（p=1，即4=3+1）、m=0，L=pm-1=1-0-1=0，L=0说明当p=1时，偶数4不能表示为两个奇素数之和，显然这个结论也符合实际；

当偶数2n=6时，6表示为两个奇数之和的表达式有3个，即6=1+5=3+3=5+1，6不能表示为素数+合数的表达形式，则p=m+L+1（p=2，即6=3+3=5+1）、m=0，L=p-m-1=2-0-1=1＞0；

当偶数2n=8时，8表示为两个奇数之和的表达式有4个，即8=1+7=3+5=5+3=7+1，8不能表示为素数+合数的表达形式，则p=m+L+1（p=3，即8=3+5=5+3=7+1）、m=0，L=p-m-1=3-0-1=2＞0；

当偶数2n=10时，10表示为两个奇数之和的表达式有5个，即10=1+9=3+7=5+5=7+3=9+1，10不能表示为素数+合数的表达形式，则p=m+L（p=3，即10=3+7=5+5=7+3）、m=0，L=p-m=3-0=3＞0.

讨论到这里有的朋友可能会问：m=0除了偶数4、6、8、10以外，是否存在更多的偶数呢？这个很可能有，但是我们不需要找出所有的偶数，并且寻找也很困难，因为随着偶数的增大，该偶数表示为素数表达式p也在增大，而m不变还等于零，所以L显然大于零.显然下文m=1也是这样.

当m=1时：

当偶数2n=12时，12表示为两个奇数之和的表达式有6个，即12=1+11=3+9=5+7=7+5=9+3=11+1，12表示为素数+合数的表达式有1个，即12=3+9，则p=m+L+1（p=4，即12=3+9=5+7=7+5=11+1）、m=1，L=p-m-1=4-1-1=2＞0；

当偶数2n=14时，14表示为两个奇数之和的表达式有7个，即14=1+13=3+11=5+9=7+7=9+5=11+3=13+1，14表示为素数+合数的表达式有1个，即14=5+9，则p=m+L+1（p=5，即1 4=3+1 1=5+9=7+7=1 1+3=1 3+1）、m=1，L=pm-1=5-1-1=3＞0；

当偶数2 n=1 6时，1 6表示为两个奇数之和的表达式有8个，即1 6=1+1 5=3+1 3=5+1 1=7+9=9+7=1 1+5=1 3+3=1 5+1，1 6表示为素数+合数的表达式有1个，即1 6=7+9，则p=m+L（p=5，即1 6=3+1 3=5+1 1=7+9=1 1+5=1 3+3）、m=1，L=p-m=5-1=4＞0；

当偶数2 n=1 8时，1 8表示为两个奇数之和的表达式有9个，即1 8=1+1 7=3+1 5=5+1 3=7+1 1=9+9=1 1+7=1 3+5=1 5+3=1 7+1，1 8表示为素数+合数的表达式有1个，即1 8=3+1 5，则p=m+L+1（p=6，即1 8=3+1 5=5+1 3=7+1 1=1 1+7=1 3+5=1 7+1）、m=1，L=p-m-1=6-1-1=4＞0；

当偶数2 n=2 4时，2 4表示为两个奇数之和的表达式有1 2个，即2 4=1+2 3=3+2 1=5+1 9=7+1 7=9+1 5=1 1+1 3=1 3+1 1=1 5+9=1 7+7=1 9+5=2 1+3=2 3+1，2 4表示为素数+合数的表达式有1个，即2 4=3+2 1，则p=m+L+1（p=8，即2 4=3+2 1=5+1 9=7+1 7=1 1+1 3=1 3+1 1=1 7+7=1 9+5=2 3+1）、m=1，L=p-m-1=8-1-1=6＞0.

在这里我们为什么不讨论偶数2 n=2 0、2 2，而直接讨论偶数2 n=2 4？因为2 0表示为两个奇数之和的表达式有1 0个，即2 0=3+1 7=5+1 5=7+1 3=1 1+9=1 3+7=1 7+3=1 9+1，2 0表示为素数+合数的表达式有2个，即2 0=5+1 5=9+1 1，所以m=2；同样可以得到，在偶数2 n=2 2中m=2，而这里专门讨论m=1，因此我们不讨论偶数2 n=2 0、2 2.

假设当m=k时，L1=p1-k＞0或L1=p1-k-1＞0（注意，通过上面讨论我们还可以发现，每一个m值可以对应多个L、p值，事实上也是这样，所以，当m=k时，L1、p1也不是对应一个L、p值，而是代表在m=k时所有L、p值.下文中L2、p2的意思也是如此）.则当m=k+1时，可设L2=p2-（k+1）或L2=p2-（k+1）-1.因为p=m+L或p=m+L+1，所以当m由k变为k+1时，p值存在3种变化情况.

1）p值增加.显然L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

2）p值减少.因为p=m+L或p=m+L+1，所以p值减少，L就减少，因为p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以p1-p2=L1-L2，或p1-p2=L1-L2-1，或p1-p2=L1-L2-2；又因为p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以p1-L1=p2-L2，或p1-L1=p2-L2-1，或p1-L1=p2-L2-2；再将式p1-p2=L1-L2、p1-p2=L1-L2-1、p1-p2=L1-L2-2的两边分别同时乘以等式p1-L1=p2-L2、p1-L1=p2-L2-1、p1-L1=p2-L2-2的两边，得到等式：①（p1-p2）（p1-L1）=（L1-L2）（p2-L2），或②（p1-p2）（p1-L1）=（L1-L2）（p2-L2-1），或③（p1-p2）（p1-L1）=（L1-L2）（p2-L2-2），或④（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2），或⑤（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2-1），或⑥（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2-2），或⑦（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2），或⑧（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2-1），或⑨（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2-2）.为了研究方便，将①化简整理得到：-L2（p2+L1）--p1p2-p1L1）=0，解之得：显然，L2＞0.同理可证，其它等式中的L2＞0.所以当m由k变为k+1、p值减少时，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

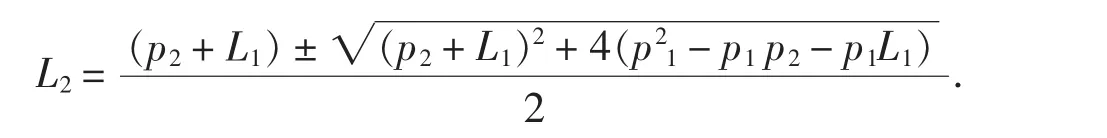
3）p值不变.因为p值不变，所以p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以，①p-L1=p-L2，或②p-L1=p-L2-1，或③p-L1=p-L2-2.再将①、②、③等式两边平方得到：④（p-L1）2=（p-L2）2，或⑤（p-L1）2=（p-L2-1）2，或⑥（p-L1）2=（p-L2-2）2.为了研究方便，将④化简整理得到：L22-2pL2+2pL1-L12=0，解之得：显然，L2＞0.同理可证，其它等式中的L2＞0.因为①、②、③等式两边均是非负数，所以通过平方后得到的④、⑤、⑥式子中L2的范围没有变化，所以当m由k变为k+1、p值不变时，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.所以当m=k+1时，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

所以当m≥0，m∈N时，公式L=p-m＞0或L=p-m-1＞0.由于L=n-2mt-2是由L=p-m或L=p-m-1推导而来，所以当n＞2，n∈N时，公式L=n-2m-t-2＞0，其中，p表示当偶数2n表为素数+素数与素数+合数或素数+1时的表达式个数（注意，在公式L=p-m中，p不包括表达式：素数+1），L表示当偶数2n表为两个素数之和时的表达式个数，n表示当偶数2n表为两个奇数之和时的表达式个数，t表示当偶数2n表为两个合数之和时的表达式个数，m表示当偶数2n表为素数+合数时的表达式个数，2m表示当偶数2n表为素数+合数及合数+素数时的表达式个数，那么公式p-m-1中最后一项1就是表示当（2n-1）是素数时，偶数2n表示为（2n-1）+1，公式L=n-2m-t-2中最后一项2就表示偶数2n表示为（2n-1）+1与1+（2n-1）.

[3] 陈景润.陈氏定理（1+2）的证明[C].北京：清华大学出版社，1973.

[5] Lu Yi.An interesting problem discovered in the properties of even numbers[J].Natural Science Research，2007，12（4）：93-95.

[6] 陆毅.对“任何一个大于4的偶数都可以表示为两个奇数之和”的思考[J].山西师范大学学报（自然科学版）研究生专刊，2008（22）：3-6.

A Proof of Representing of an Even Number as Summation of Two Odd Numbers

LU Yi

(Fangshan High school，Tonghai，Lianyungang 222341，Jiangsu，China)

An even number is represented as a summation of two odd numbers in 6 expressions.The relationship among the expressions are demonstrated and proved with mathematical induction.

odd number expression；prime number expression；summation；number of expressions

O 156.4

A

1001-4217（2010）01-0001-07

2009-10-09

陆毅（1967-），男，江苏连云港人，本科.研究方向：解析数论-哥德巴赫猜想.E-mail：luyi1967314@163.com