一个不等式约束问题的SQP方法及其收敛性

解才先，朱宁

（桂林电子科技大学数学与计算科学学院，广西桂林541004）

一个不等式约束问题的SQP方法及其收敛性

解才先，朱宁

（桂林电子科技大学数学与计算科学学院，广西桂林541004）

提出一个关于不等式约束问题的SQP算法，其效益函数为非可微精确罚函数，罚因子具有自动调节性.通过求解一辅助线性方程组，获得二阶修正步，并利用弧式搜索，建立了问题的一个可行下降算法.在一定的假设条件下，证明了算法是全局收敛的，并且具有超线性收敛速度.

SQP方法；弧式搜索；非可微精确罚函数；全局收敛性；超线性收敛性

0 引言

序列二次规划（SQP）算法是解非线性最优化问题的最有效方法之一，自上世纪70年代以来一直是非线性领域的一个研究热点[1-8].但是，如果不等式约束优化问题对应的二次子问题无可行解，或者它即使有解，但其解为无界时，则该方法失败或产生一个不收敛的点列.针对这个问题，研究者提出了一些解决方法.Zhang等[5]提出，当二次子问题无可行解或者有解但无界时，通过解一线性规划获得搜索方向，在一定假设条件下，获得了算法的全局收敛性.本文在文献［5］的基础上对算法进行了进一步的修正，通过求解一辅助线性方程组获得二阶修正步，并利用弧式搜索，在一些微弱假设条件下，证得单位步长是可以接受的，从而克服了Maratos效应，最终得出该算法还具有超线性收敛速度.

1 算法模型

本文考虑如下不等式约束优化问题：

其中f:Rn→R，g:Rn→Rm是二阶连续可微的.求解问题（1）的SQP方法是一个迭代算法，每一步迭代中其搜索方向dk是通过求解下列二次子问题所得：

这里Bk是一对称正定矩阵.迭代具有下列形式：xk+1=xk+tkdk，其中tk是通过对效益函数采取一维搜索所得的步长.令：

Φ（x）沿着d∈Rn的方向导数为：

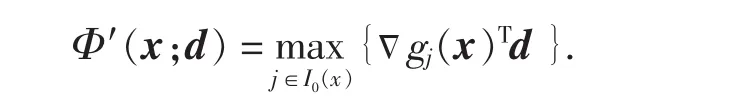
其中I0（x）=｛j:gj（x）=Φ（x），j∈M∪｛｝0｝，通常来讲，Φ′（x；d）是不连续的.文献［6］提出了Φ′（x；d）的一个连续逼近Φ*（x；d），即：

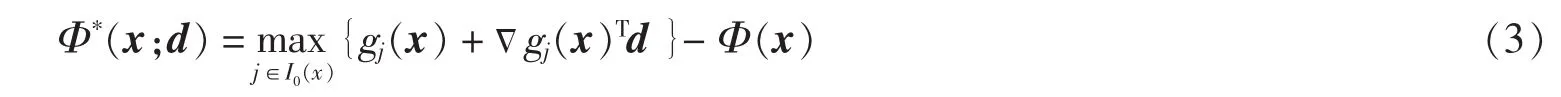
这里，称式（3）为Φ（x）沿着方向d的伪方向导数，很容易证明Φ*（x；d）在Rn×Rn上是连续的[6].

引理1[7]∀x,d∈Rn，有Φ*（x；d）≥Φ′（x；d），且Φ*（x；·）为Rn上的凸函数.令：

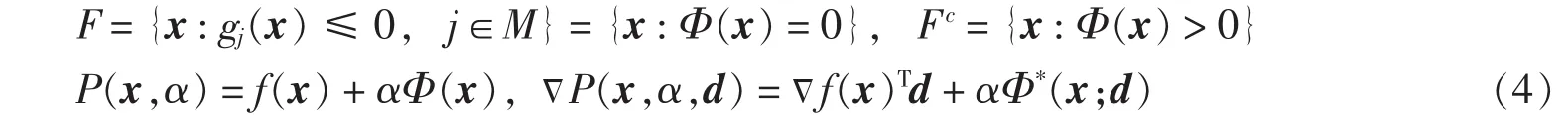
定义1 （广义MFCQ）[5]令x∈Fc，如果∃z∈Rn，‖z‖=1和δx＞0，使得：成立，则称在x处满足广义MFCQ.

当x∈Fc，求解下列线性规划：

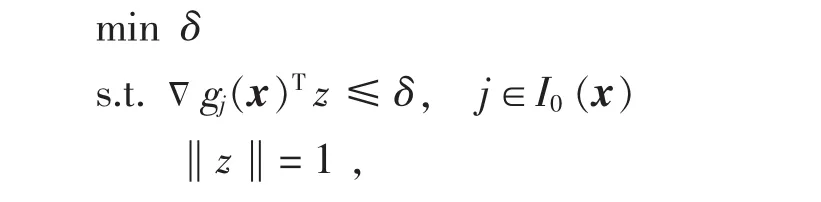
令d（x，B）为下面二次规划Q（x，B）的解：

这里B是一对称正定矩阵.

引理2i）若Q（x，B）是可行的，则式（5）有唯一解d（x，B）.

ii）若d（x，B）为Q（x，B）的解，当且仅当存在一Lagrange乘子λ∈Rn，使得：

（S0）给定数据x1∈Rn，u∈（0，），B1对称正定，α1，0为初始步长，M1为对初始搜索方向dk范数的要求，σ，σ1分别为步长αk及Mk的增长倍数，α1，0＞0，M1＞0，σ＞1，σ1＞1，令k:=1；

（S1）令i:=0和tk，0=1，解式（2）计算dk，若式（2）不可行或xk∈Fc且‖dk‖＞Mk，转（S5），若dk=0，停；

（S2）若ΔP（xk，αk，i，dk）≤转（S4）；

（S3）αk，i:=σαk，i，若P（xk，αk，i）＞P（x1，αk，i），转（S9），否则，转（S2）.

转（S8），其中ωk表示搜索方向，这里为

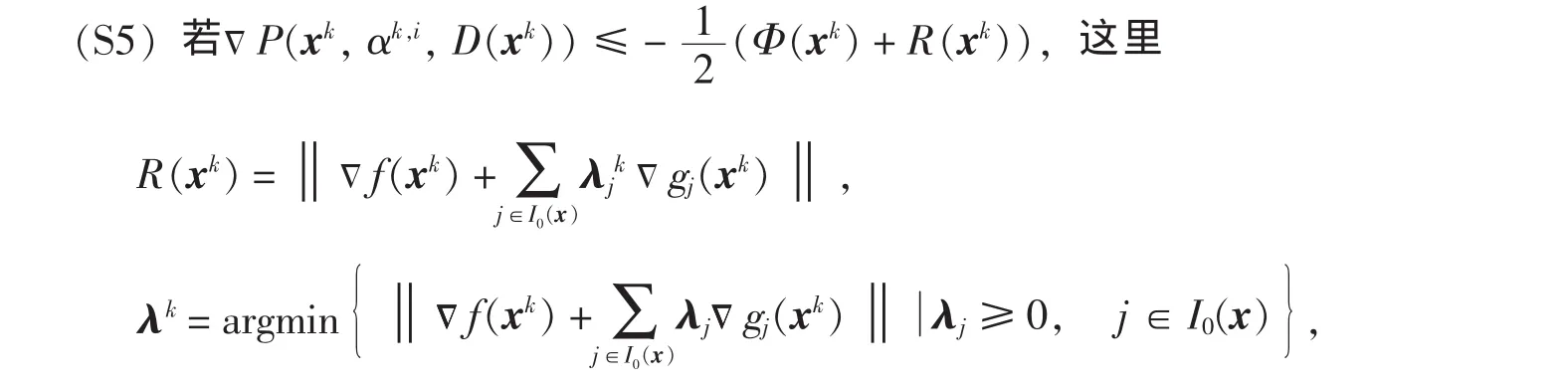
转（S7）；

转（S8），否则，i:=i+1，αk，i:=αk，i-1，选择tk，i:=转（S7）；

（S8）令αk+1，0:=αk，i（为方便起见，记ik=i，αk=αk，i，tk=tk，i），xk+1=xk+tkωk，Mk+1:=Mk，利用BFGS校正[9]公式产生Bk+1，令k:=k+1，转（S1）；

（S9）令αk，0:=αk，i，xk:=x1产生一个新的Bk，转（S1）.

2 算法可行性

在以下的分析中，假设如下条件成立.

假设Ai）{xk}是一有界序列；

ii）∀x∈F，积极约束的梯度线性无关；

iii）∀x∈Fc，广义MFCQ在x处成立；

iv）∀k，Bk为属于一对称正定矩阵的紧致集Σ中的有界序列，且存在常数0＜b1≤b2＜∞，使得b1‖dk‖2≤（dk）TBkdk≤b2‖dk‖2，∀dk∈Rn，k=1，2，…成立.

由命题1，容易得以下定理.

定理1若算法在（S1）终止于xk，则xk是问题（1）的K－T点.

命题2[8]若假设A成立，是一可行点，是一对称正定矩阵，则d（x，B）在（，）的一个领域内有定义且在（）上连续.

命题3[5]算法不会在（S2）和（S3）之间无限循环.

命题4[5]算法不会在（S5）和（S6）之间无限循环.

命题5算法不会在（S4）之间无限循环.

证明由命题3的证明，当i充分大时，有αk，i=.现假设算法在（S4）之间无限循环，则必有tk，i→0，i→∞.而且

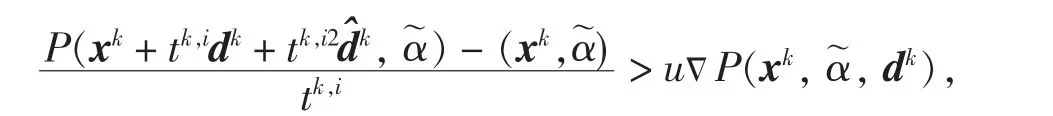
令i→∞，有：

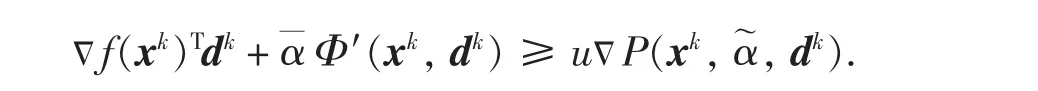
由引理1和式（4），可得

但是由（S2），可得

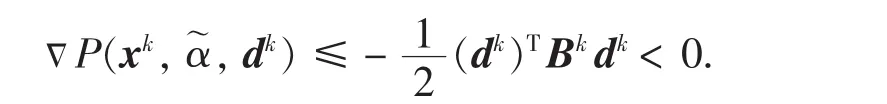
结合式（9），这与0＜u＜1矛盾，证毕.

命题6[5]算法不会在（S7）之间无限循环.

3 超线性收敛性

为证算法具有超线性收敛性质，还需作如下假设.

假设Bi）｛xk｝→；

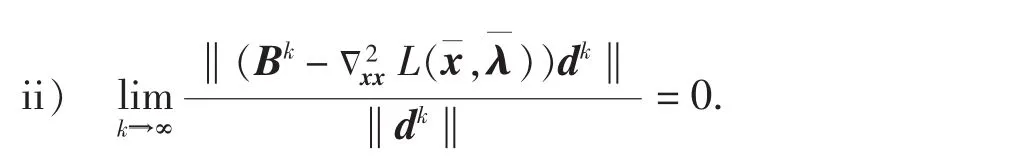
由命题1，可得以下引理.

引理3（dk，λk）→（0，），在这里，）是问题（1）的K－T对，（dk，λk）是问题Q（xk，λk）的K－T对.

证明类似文献［10］中命题4.1.

引理5假设｛xk｝为算法在弧式搜索下产生的无穷序列.若假设A和假设B成立，则当k充分大时，步长tk=1.

证明由引理4和‖dk‖→0，k→∞.当k充分大时，可得：‖‖≤‖dk‖由假设A ii）可得，当k充分大时，≠0.

结合命题3和命题5，要证明当k充分大时步长tk=1，只要证明

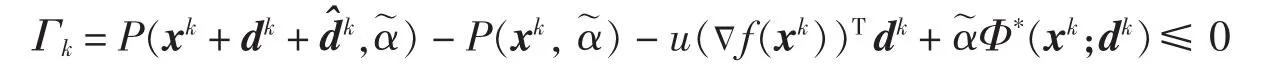
成立即可.

因为‖dk‖→0，k→∞和引理4，有：

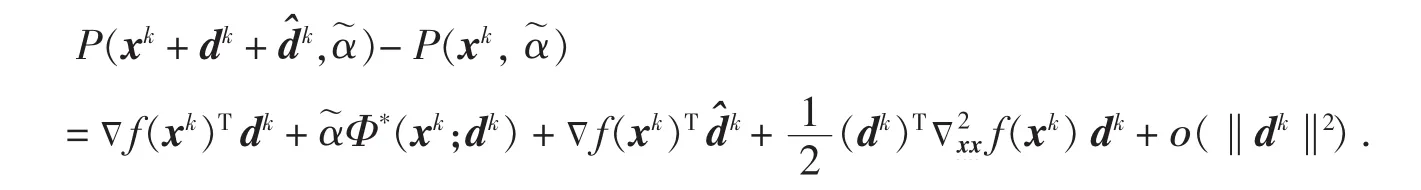
由式（6）和引理3，可得：

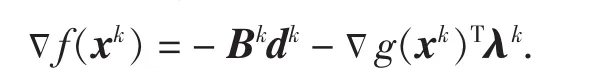
由Bk的有界性，引理4以及的定义式（8），有：

由式（4）、（7）和（S2），知：

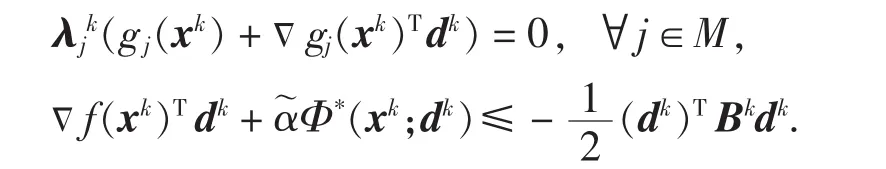
所以：

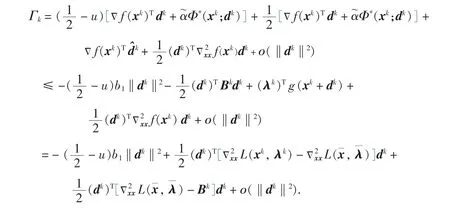
因为xk→¯，λk→和假设B（ii），可得:

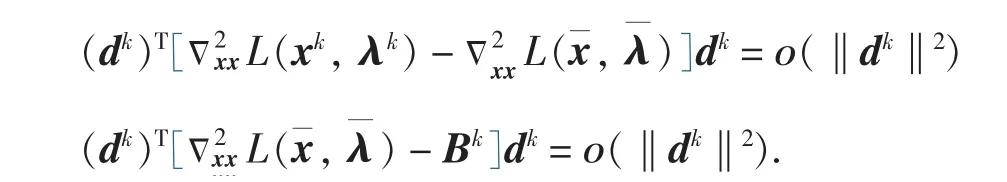
因此当k充分大时：

定理2若引理5条件成立，则｛xk｝超线性收敛于x¯，即：

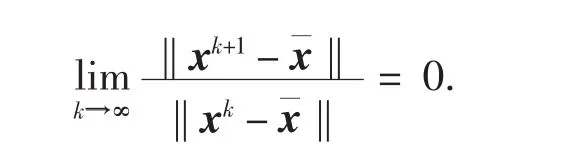
证明由文献［9］中定理12.7.5，有：

由引理5知，当k充分大时，tk=1成立.因此：

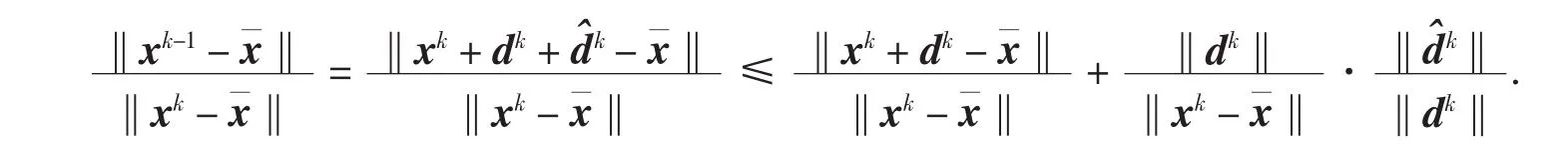
4 结语

在该算法下，类似于文献［5］可以很容易证明仅在假设A条件下，该算法具有全局收敛性.但是当x不可行时，如何构造一个更有效的线性规划来求解出搜索方向D（x），还有待于进一步研究.

[1] Che Jianren，Su Ke.A modified SQP method and its global convergence[J].Applied Mathematics and Computation，2007（186）：945-951.

[2] Xue Wenjuan,Shen Chungen，Pu Dingguo.A penalty- function- free line search SQP method for nonlinear programming[J].Journal of Computational and Applied Mathematics，2009（228）：313-325.

[3] Zhu Zhibin,Zhang Kecun，Jian Jinbao.An improved SQP algorithm for inequality constrained optimization[J].Mathematical Methods of Operations Research,2003（58）：271-282

[4] Su Ke，Yu Zhensheng.Amodified SQP method with nonmonotone technique and its global convergence[J].Computers and Mathemativs with Applications，2009（57）：240-247.

[5] Zhang Juliang，Zhang Xiangsun.A SQP method for inequality constrained optimization[J].Acta Mathematicae Applicatae Sinica，2002，18（1）：77-84.

[6] Bazaraa M S，Goode J J.An algorithm for solving linearly constraint minimax problem[J].EJOR，1982（11）：158-166.

[7] Zhou Guanglu.A modified SQP method and its global convergence[J].Journal of Global Optimization，1997（11）:193-205.

[8] Facchinei F.Robust recursive quadratic programming algorithm model with global and superlinear convergence properties[J].JOTA，1997（92）:543-579.

[9] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，1997.

[10] DE Q Pantoja J F A.Mayne D Q.Exact penalty function algorithm with simple updating of the penalty parameter[J].JOTA，1991，69（3）:441-467.

A SQP Method for Inequality Constrained Optimization and Its Convergence

XIE Cai-xian，ZHU Ning

(School of Mathematics and Computing Science,Guilin University of Electronic Technology,Guilin 541004,Guangxi，China)

In this paper，a SQP method,in which the merit function is nondifferentiable exactpenaltyfunction，ispresentedtosolveinequalityconstraint.Thepenaltyis adjusted automatically.The arc- search and the second- order correction，which is obtained by solving an auxiliary linear equation system，are used to obtain a feasible descent algorithm.Under some suitable assumptions，it is proved that the convergence of the algorithm is global as well as superlinear.

SQP method；arc- search；nondifferentiable exact penalty function；global convergence；superlinear convergence

O221.2

A

1001-4217（2010）01-0017-07

2009-11-05

解才先（1985-），男，山东临沂人，硕士研究生.研究方向：优化及应用.E-mail:xiecaixian1@163.com