基于Baker映射迭路的图像加密算法

叶瑞松，庄乐仪

(汕头大学数学系,广东汕头515063)

基于Baker映射迭路的图像加密算法

叶瑞松，庄乐仪

(汕头大学数学系,广东汕头515063)

提出一种基于Baker映射迭路的数字图像空间域的编码新方法，利用Baker映射迭路所得的有限符号串对图像像素位置编码，从而对数字图像进行置乱，并计算置乱周期和置乱度.在此基础上，利用Logistic映射的混沌性质对置乱图像作了进一步的加密.

Baker映射；迭路；置乱；加密

0 引言

数字图像置乱在信息隐藏的前处理或者后处理当中是一种常见的处理方法，许多学者提出了有效的置乱方法，如Chen等人[1]用3D混沌映射做图像加密的置乱处理，丁玮等人[2]利用Arnold变换置乱图像，王笋等人[3]则利用FASS曲线扫描的方法置乱.Baker映射是一种混沌映射[4]，因此也被广泛应用到图像的置乱加密.茅耀斌等人[4]提出了将离散的二维Baker映射用于图像置乱，并推广到三维的情形用于图像加密[5].赵学峰[6]则结合帐篷映射的折叠方式提出了一种新的离散型Baker变换图像置乱.

本文以符号动力学为工具，提出了将构造的Baker映射迭路应用于图像像素位置的编码，并对图像进行置乱的方法.与邹建成等人[7]的置乱方法做比较，结果显示本文的方法效果明显较佳.在此基础上，利用Logistic映射的混沌性质对置乱图像做进一步的加密，扩散图像的灰度值以抵抗统计分析的攻击.

1 相关知识

1.1 迭路

符号动力学指出，如果动力系统的某轨道一定通过一列不同的区间，将每个区间用一个符号对应表示，那么就得到这条轨道的迭路[8].

定义设映射F是从集合X到其自身的函数，Λ为X的子集，如果：

i）若x∈Λ，则F（x）∈Λ；

ii）对于任一点b∈Λ，都存在一点a∈Λ，使得F（a）=b.则称子集Λ为F的不变集，即F（Λ）=Λ.

设函数F的不变集Λ=H0∪H1∪…∪HN，满足int（Hi）∩int（Hj）=ø，对任意的i≠j成立，其中，i，j=0，1…，N，N∈Z+.由定义，任一点x∈Λ必对所有的j∈Z满足Fj（x）∈Ht， 其中t=0，1，…，N.由此可得任一点x∈Λ对应的符号串如下:即对于所有的j∈Z，Fsj（x）∈Hsj，故x∈F-j（Hsj），且称无限双边符号串s=…s-2s-1·s0s1s2…为点x的迭路.定义迭标映射h:Λ→Σ为s=h（x）.

1.2 Baker映射

Baker映射是一个综合压缩、拉伸、翻转和折叠的映射，具有混沌的性质，受到数学家、物理学家和其他从事非线性研究的科研工作者广泛关注[7].下面构造的两个Baker映射将用于产生有限的符号串作为图像空间位置的编码.

1.2.1 二进制Baker映射

首先考虑如式（2）、（3）所示的二进制Baker映射及其逆映射.

显然，区域Λ=［0，1］×［0，1］为式（2）、（3）的不变集.将该区域划分为两个互不相交的区域H0：，从而得到任一点x∈Λ相应的迭标映射:

其中sj由式（1）决定，j∈Z，式（1）中取N=1.式（2）在y轴上像帐篷映射一样分段扩张，在x轴上压缩；而式（3）刚好相反，在x轴上分段扩张，在y轴上压缩，故与文献［8］中介绍的几何马蹄映射F是相似的，不同之处在于映射F的不变集ΛF是Cantor集,而式（2）、（3）的不变集Λ=［0，1］×［0，1］.Robinson[8]指出，迭标映射hF:ΛF→Σ2是一一对应的.故任一区域，都有唯一的有限符号串s-n…s-1·s0…sn-1与之对应，即对应的二进制编码（s0…sn-1，s-n…s-1）唯一，其中，sj=0，1（j=-n，…0，1，…，n-1）.这就保证用此方法对图像像素点编码是一一对应的.1.2.2三进制Baker映射

可将二进制Baker映射推广到三进制，甚至是K进制的情况，并利用其迭路产生的有限符号串作为图像像素点的K进制编码.若对区域Λ=［0，1］×［0，1］从上至下划分为3等分，即和H2：，仍然将压缩、拉伸、翻转和折叠应用于这3个子区域，则可得到三进制Baker映射式（5）及其逆映射式（6）:

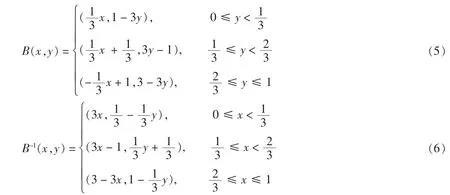
不变集仍为区域［0，1］×［0，1］，式（1）中取N=2.同样用式（5）、（6）的迭路对图像像素点编码也是一一对应的.Baker映射还可有其他形式，只是式（2）和式（5）的迭路较为复杂，置乱效果较好.如何构造简单的K进制Baker映射的具体形式见文献［9-10］.

2 编码过程

由于二维数字图像的像素总数总是有限的，取有限符号串即可为各像素位置编码,而编码的长度是由图像的大小所决定的.采用K进制Baker映射的迭路进行编码时,可得到KM×KM个不相交的区域int（Vs-M…s-1·s0…sM-1），其中M∈Z+，sj=0，1，…，K-1.图像大小的选取也应该是KM×KM，以保证编码是一对一的.

下面以2M×2M图像为例（M∈Z+），叙述采用二进制Baker映射的迭路编码的步骤.其中Ht的选取（t=0，1）如前面第1节所述.

步骤1令迭代次数k=0.对于每一像素位置（i，j），读取行、列数均为n=2M的图像，取相应迭代初始点若点（x0，y0)令s0=t，其中t=0，1.

步骤2令k=k+1，将点（xk-1，yk-1）代入式（2）得到点（xk，yk）.若点（xk，yk）∈Ht，则令sk=t，其中t=0，1.

步骤3重复步骤2，直到k=M-1.得到有限符号串s0s1s2…sM-1.令k=0.

步骤4令k=k+1，将点（x-（k-1），y-（k-1））代入式（3）得到点（x-k，y-k）.如果点（x-k，y-k）∈Ht，则令s-k=t，其中t=0，1.

步骤5重复步骤4，直到k=M.得到有限符号串s-M…s-2s-1.

由上述步骤可得到所有像素位置的二进制编码（s0s1…sM-1，s-M…s-1），将其转换为十进制，即为（i，j）上像素的新位置.因为Vs-M…s-1·s0…sM-1，而用于迭代的初始点满足（x0，y0）∈int（），其中i，j=1，2，…，n，所以编码是唯一的.这就保证了图像置乱的可逆性.

三进制Baker映射（或K进制Baker映射）进行编码的步骤与上面类似，为保证编码的唯一性，选取的迭代初始点应该在in t（）中，否则若选在边界上可能会出现迭路不唯一的情况[8].

3 仿真实验

3.1 二进制编码置乱

选用256×256的灰度LENA图像，见图1（a），作为实验对象，将其像素矩阵记为I（大小为28×28）.记置乱后的图像矩阵为I′.用第2节中编码方法为I中各像素位置（i，j）编码，并将编码转化为十进制数对（Rij，Cij），令I′（Rij，Cij）＝I（i，j），即可得到置乱的图像.图1（b）～（d）为所得的置乱结果.

图1 二进制Baker映射迭路编码的置乱结果

由图1可看出,置乱2次可达到较好的效果.表1为本算法（记为算法1）与邹建成等人[7]的二进制Baker映射置乱算法（记为算法2）应用于不同大小图像置乱的周期比较.

表1 置乱算法周期

由表1可看出，算法1对于2N×2N大小的图像（N＝2，3，…，10）置乱周期较算法2好.下面对256×256的LENA灰度图（图1（a））采用卢振泰等[11]给出的置乱度求法进行数值实验，绘制一个周期内两种算法置乱度的变化曲线，如图2所示.数值结果表明，算法1在一个周期内对图1（a）的置乱度较算法2稳定，迭代较少的次数即可达到较好的置乱效果,置乱周期也较长.

3.2 三进制编码置乱

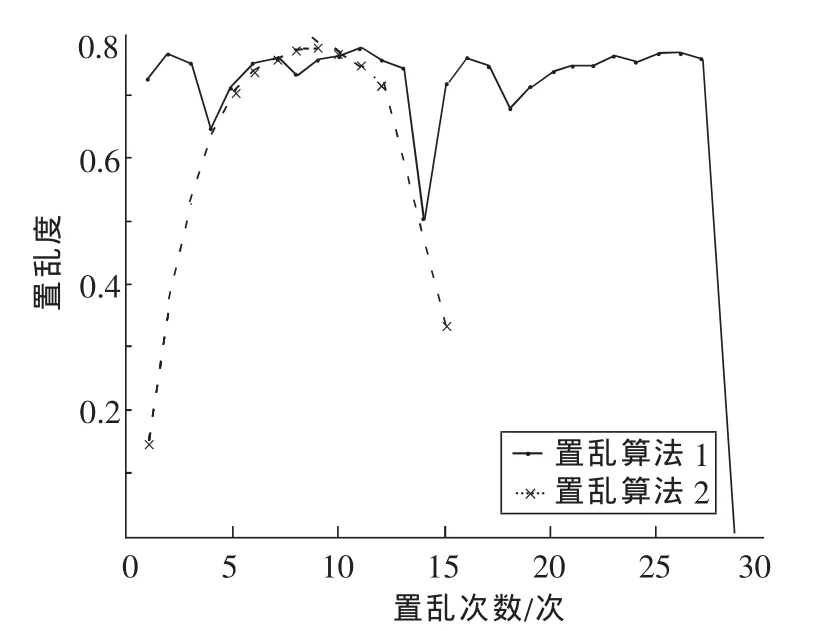
图2 两种置乱方法置乱度比较

如图3（a）选用243×243的灰度LENA图像（即大小为35×35）.结合式（5）、（6），以第2节中提出的方法为I中各像素位置（i，j）编码，并将三进制编码转化为十进制数对（Rij，Cij），令I′（Rij，Cij）＝I（i，j），即可得到置乱的图像I′.图3（b）～（d）为置乱结果，置乱周期达到2 604.

图3 三进制Baker映射迭路编码的置乱结果

3.3 灰度值扩散

为了抵抗统计分析等攻击，这里利用Logistic映射式（7）在μ取（3.569 9…，4］时产生的数列处于混沌状态的特点[8，12]，生成一个伪随机矩阵C，用于扩散置乱后图像的灰度值，达到加密的目的.灰度值的扩散采用按位异或，加法和取模的算法[1].

由式（7）的特点，选择参数μ、初始值x0和加密次数n作为密钥对图像进行加密，图像加密的具体过程如下.

步骤1采用3.1节提出的二进制编码置乱方法将原图像I置乱一次得到图像I′.

步骤2由式（7），取初始值x0∈（0，1），μ＝4，产生一个与原图像等大的随机矩阵C（记其行数为r，列数为c），令C＝floor（L·C），其中，L为该图像的灰度级.

步骤3用式（8）、（9）扩散I′的灰度值.

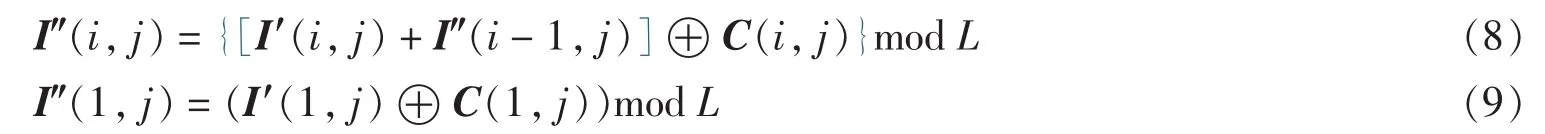
其中2≤i≤r，1≤j≤c，L为图像的灰度级，⊕表示按位异或运算.重复上述步骤k次可得到加密k次的图像I″.式（8）、（9）的逆变换为:

解密为上述过程的逆过程.图4（b）～（d）为对256×256大小的NA灰度图加密解密结果，加密次数为3次，密钥x0=0.712 345 678 901 234 5，错误解密的密钥为x0′=0.712 345 678 901 234 6，可见10-16的差别就不能正确解密，密钥空间为10-16.图4（e）～（h）为加密前后对应的灰度值直方图.

图4的实验结果显示，加密后图像的灰度直方图能够较均匀地分布，正确解密结果与原图信息一致.随机选取图像中1 000对相邻的像素，计算原图和密图的相关系数如表2所示.由表2可看出，该算法能够有效地削弱图像相邻点之间的相关性.

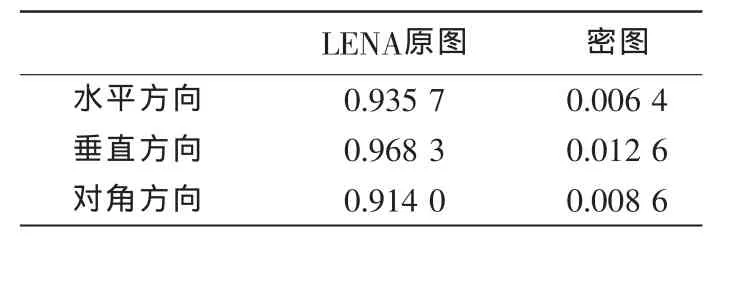
表2 LENA原图和密图的相关系数

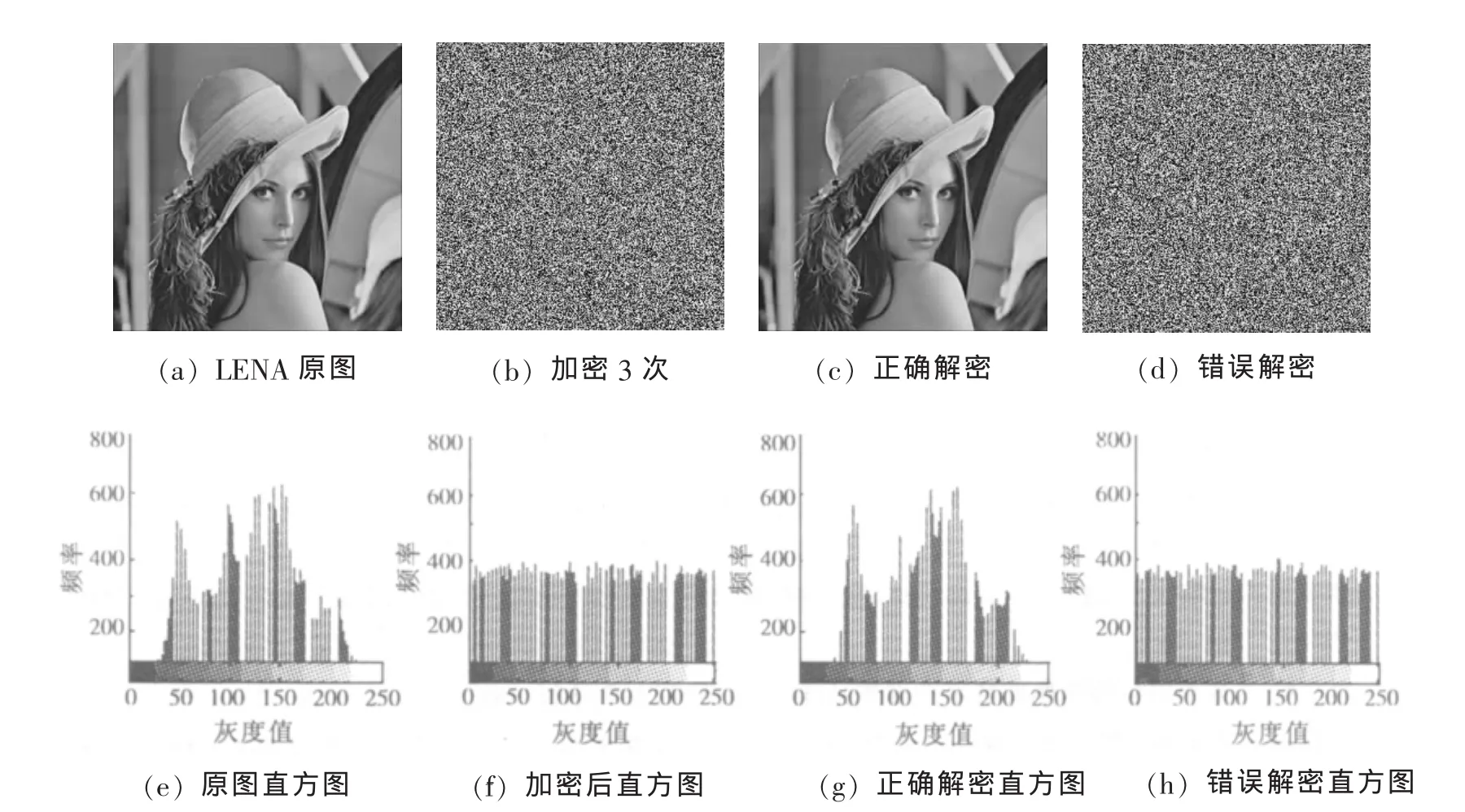
图4 LENA图三次加密、解密图像及对应直方图

最后我们测试了明文一个像素的改变对密文的影响，图5为像素变化率NPCR[1]和归一化平均变化强度UACI[1]随加密次数增加的变化图.总体来看,随着加密次数增加，一个像素的改变对密文图像的影响加大.

图5 NPCR和UACI变化图

4 结语

与常用的利用离散Baker映射或者其截断变换进行置乱不同，本文利用Baker映射产生的迭路对图像各像素位置进行编码，得到编码矩阵用于将数字图像置乱，避免了由计算机精度问题导致多次变换后图像像素值丢失的情况.数值实验表明，与邹建成等[7]的二进制Baker映射置乱方法比较，本文利用二进制Baker映射的迭路编码的方法在稳定性和置乱周期都有优势.最后利用Logistic映射混沌性质对置乱后图像灰度值进行扩散，得到进一步加密的图像.

[1] Chen Guangrong,Mao Yaobin,Chui Charles K.A symmetric image encryption scheme based on 3D chaotic cat maps [J].Chaos,Solitons and Fractals,2004（21）：749-761.

[2] 丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学报，2001，13（4）：338-344.

[3] 王笋,徐小双.Hilbert曲线扫描矩阵的生成算法及其MATLAB程序代码[J].中国图象图形学报,2006,11（1）：119-122.

[4] 茅耀斌，戴跃伟,王执铨.一种基于Baker映射的图像信息隐藏方法[J].南京理工大学学报，2002，26（2）：152-156.

[5] 廉士国,茅耀斌,王执铨.Baker映射三维扩展及其在多媒体加密中的应用[J].控制与决策,2004,19（6）：714-717.

[6] 赵学峰.基于面包师变换的数字图像置乱[J].西北师范大学学报,2003，2（39）：26-29.

[7] 邹建成，齐东旭,熊昌镇.基于面包师变换的数字图像加密[J].北方工业大学学报，2003，15（1）：6-10，61.

[8] Clark R R.动力系统导论[M].北京：机械工业出版社，2007.

[9] 熊昌镇，邹建成.K进制面包师变换及其在数字图像加密中的应用[J].北方工业大学学报，2004，16（1）:6-11.

[10] Fidrich J.Symmetric ciphersbasedon two- dimensional chaotic maps[J].International Journal of Bifurcation and Chaos，1998，8（6）：1 259-1 284.

[11] 卢振泰，黎罗罗.一种新的衡量图像置乱程度的方法[J].中山大学学报（自然科学版）,2005（44）:126-129.

[12] 叶瑞松，郗坤洪.一种基于混沌序列控制的3D cat映射加密算法[J].汕头大学学报（自然科学版），2007，22（2）:65-70.

Encryption Algorithm Based on the Itinerary of Baker Map

YE Rui-song，ZHUANG Le-yi
(Department of Mathematics，Shantou University，Shantou 515063，Guangdong，China)

A novel digital image encoding approach based on the itinerary of Baker map in spatial domain is proposed.It uses the finite character strings generated by the itinerary of Baker map to encode the pixels’positions so as to scramble the image.The periods and scrambling degrees of the algorithm are calculated as well.Furthermore，the chaotic characteristics of the Logistic map are applied to encrypt the scrambled image.

Baker map；itinerary；scrambling；encryption

TP 391.41

A

1001-4217（2010）01-0054-07

2009-06-09

叶瑞松（1968-），男，福建漳州人，教授.研究方向：分歧理论及其数值计算，分形混沌及其计算机应用.E-mail：rsye@stu.edu.cn