一类二阶变系数线性微分方程的算子解法

方书盛

（汕头市达濠第二中学，广东汕头515071）

一类二阶变系数线性微分方程的算子解法

方书盛

（汕头市达濠第二中学，广东汕头515071）

运用微分算子的理论和方法研究了二阶变系数线性微分方程的解法；在一定的条件下利用算子解法求出一类二阶变系数线性微分方程的通解；应用所得结果推导出已知类型方程可用算子解法求出通解的一些可积类型；举例说明使用算子解法求出已知类型方程通解的步骤和方法.

二阶；变系数；算子解法；可积类型

0 引言

二阶变系数线性微分方程在自然科学与工程技术中有着广泛的应用[1].因此，研究二阶变系数线性微分方程的求解方法，具有重要的应用价值和理论意义.

由于一个二阶变系数线性微分方程的可积与对应的一个Riccati方程的可积是等价的（参见本文引理1及引理2），然而Riccati方程在一般情况下是不可积的[1-2]，因此，二阶变系数线性微分方程在一般情形下是不可积的，即在一般情形下，方程的解不可能用有限形式的初等积分来表示.但某些特殊形式的变系数线性方程还是可积的，例如著名的Euler方程.为了适应理论研究和工程应用的需要，近30年来，人们用不同的方法不断探索二阶变系数线性方程的各种特殊的可积类型，至今已取得了一系列成果[3-10].本文作者在文献［3］中给出了任意阶的变系数线性方程的算子解法，这种解法是求出某些特殊形式的变系数线性方程的一种简便实用的方法.本文运用文献［3］的结果，研究了一类重要的二阶变系数线性方程的解法，得到了已知类型方程的一些可积类型.

1 预备知识

文献[3-4]中已给出了二阶线性微分算子的分解及二阶变系数线性微分方程算子解法的一些结果，下面引用其中的一些结果.

引理1[3]二阶变系数线性微分方程

可积的充分必要条件是，已知方程左端微分算子可分解为两个有限形式的一阶微分算子因式的乘积：

引理2[4]二阶变系数线性微分算子

可分解成有限形式分解式（1）的充分必要条件是Riccati方程

是可积的，这时b（x）=y（x），a（x）=p（x）-y（x）.

定义1[3]一个已知函数f（x）除以一阶微分算子D+p（x）所得结果为：

其中c表示任意一个常数.

2 主要结果

考虑如下形式的二阶变系数线性齐次方程：

以下先证明本文主要结果的一个定理.

定理1如果多项式p（x）及q（x）满足条件：

其中a（x），b（x）分别是x的特定函数，那么方程（4）是可积的，其通解是：

其中c1，c2分别是任意的常数.

证明对于不等于零的x值，方程（4）的两边同时除以x2并且用算子形式表示为：

当p（x）及q（x）满足已知条件时，由式（5）得到：

将所得式子代入式（6）得到：

于是Riccati方程（2）是可积的，由引理2可知，方程（4）变形后所得方程（7）的左端微分算子可分解为有限形式的因式的乘积，由式（1）得到：

因此，方程（7）可表示为：

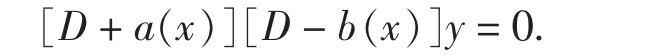
利用定义1 ，所得方程两边同除以一阶微分算子D+a（x），由式（3）得到：

再次利用定义1 ，所得方程两边同除以一阶微分算子D+b（x），由式（3）得到已知方程（4）的通解：

定理1证毕.

作为定理1的推论，可得到以下一些结果.

推论1[11]如果已知多项式p（x）及q（x）满足条件：

那么方程（4）是可积的，其通解是：

证明取函数a（x），b（x）分别为a（x）=0，b（x）=则有：

于是定理1的条件满足，从而由定理的结论可得，方程（4）是可积的，其通解是：

推论1证毕.

推论2[11]如果已知多项式p（x）及q（x）满足条件

其中k为不等于零的常数，那么方程（4）是可积的，其通解为：

证明取函数a（x），b（x）分别为：

则有：

从而定理1的条件满足，所以由定理的结论可得，已知方程（4）是可积的，其通解为：

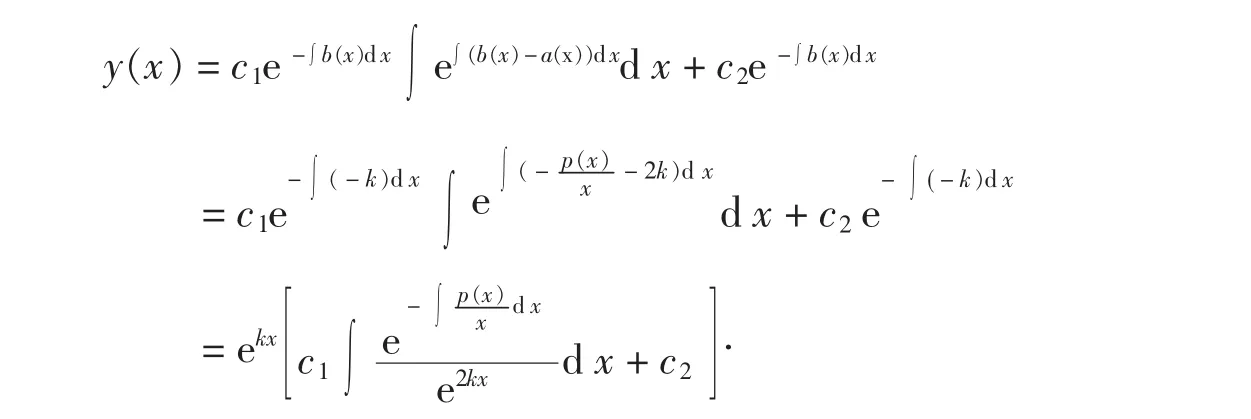
推论2证毕.

3 实例

例1用算子解法求出以下微分方程的通解：

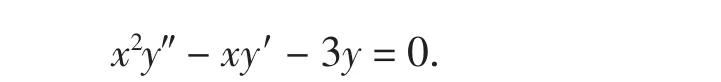
解已知方程对应于方程（4）的函数p（x）及q（x）分别是：p（x）=－1，q（x）=-3，取则有；

这时满足定理1的条件，所以由定理的结论可得，已知方程是可积的，其通解为：

例2用算子解法求出以下微分方程的通解：

解已知方程对应于方程（4）的函数p（x）及q（x）分别是：

所以可得：

这时满足推论1的条件，所以由推论1的结论可知，已知方程是可积的，其通解为：

4 结语

本文给出的算子解法不仅可用于求解特殊形式的一类二阶变系数线性方程，同时也适用于求解一般形式的二阶变系数线性方程，对于在科学技术中常遇到的二阶变系数线性方程求解有很大的帮助.另外，必须说明的是，本文所得到的已知类型方程的可积类型，只是这类方程的几种较重要的可积类型，不可能包括各种不同的可积类型.在实际应用中，用同样的方法可推导出其它更多的可积类型，限于篇幅，这里不再一一列出.

[1] 李文荣，张全信.函数方程与微分方程的解析解[M].北京：科学出版社，2008.

[2] Krasnov M L，Kiselyov A I，MakarenKo G I.A book of problems in ordinary differential equations[M].Moscow：Mir Publishers，1983.

[3] 方书盛.变系数线性微分方程的算子解法[J].数学的实践与认识，2004，34（7）：159-165.

[4] 黎耀善.二阶线性微分算子的分解及其应用[J].数学的实践与认识，1989（2）：56-62.

[5] Ramankutty P.The complementary funtion and the general solution[J].Mathematics Magazine，1991，64（2）：124-130.

[6] 李鸿祥.常微分方程的一些新的可积类型[J].数学的实践与认识，1980，10（1）：46-51.

[7] 章联生.高阶变系数线性微分方程的一些新的可积类型[J].数学的实践与认识，2009，39（15）：229-234.

[8] 宁荣健，唐烁，朱士信.一类二阶变系数线性微分方程的积分因子解法[J].大学数学，2006，22（2）：123-126.

[9] 王黎辉.一类二阶变系数线性微分方程及其解的构造方法[J].大学数学，2006，22（5）：146-149.

[10] 何众琦.两类可积的二阶线性方程[J].高等数学研究，2008，11（3）：5，28.

[11]冯录祥.一类Riccati方程的推广[J].数学的实践与认识，2003，33（5）：115—119.

The Operator Method to Solve a Type of Linear Differential Equations of the Second Order with Variable Coefficients

FANG Shu-sheng

（Dahao Second Middle School of Shantou，Shantou 515071，Guangdong，China）

A technique of the operator to solve a type of linear differential equations of the second order with variable coefficients is given.The integrable type is discussed which is enabled to use the operator method to find the general solution of given differential equation.

second order；variable coefficients；operator method；integrable type.

O 175.1

A

1001-4217（2010）01-0012-06

2009-05-19

方书盛（1945-），男，广东普宁人，大学本科，高级教师.研究方向：微分方程的解析解.E-mail：sh_fang1212@163.com