蛋白质序列混沌游戏表示模拟效果的优化

肖前军，周金玉，邓总纲

(湖南理工职业技术学院，湖南湘潭411104)

蛋白质序列混沌游戏表示模拟效果的优化

肖前军，周金玉，邓总纲

(湖南理工职业技术学院，湖南湘潭411104)

蛋白质序列的可视化表示——混沌游戏表示呈现出明显的分形特征.根据分形的产生机理，可以用递归迭代函数系统很好地模拟蛋白质序列的混沌游戏表示.在实验中发现，其模拟效果可以进一步优化，可能有助于更准确地进行物种亲缘关系的分析.

递归迭代函数系统；混沌游戏表示；模拟；蛋白质序列；优化

0 引言

蛋白质序列是由20种不同的氨基酸组成的一维字符序列，但要直接从中得出更多隐含的生物特性是非常困难的.为此人们设计出很多方法来进行序列分析，例如，统计分析、人工神经网络技术和动态规划等方法已经成功地应用到蛋白质序列分析的某些领域，但这些方法不够直观且其中很多方法都需要进行繁琐的序列比对.因此，人们探索将蛋白质序列转化为数字信号、曲线或者可视化模型，再利用数学方法（如分形理论）进行相关分析，以期从中发现更多的生物特性.Jeffrey[1]介绍了一种表征蛋白质序列的可视化方法——混沌游戏表示，通过在蛋白质序列的混沌游戏表示图中发现明显的分形特征[2-5]，而实际的分形是随机迭代产生的，因此可以运用递归迭代函数系统[2，5-10]来模拟蛋白质序列的混沌游戏表示.实验发现模拟效果很好[2，7]，而且其结果可以进行物种进化等相关分析[6]，实验过程中还发现其模拟结果可以进一步优化.

1 理论模型

1.1 蛋白质序列混沌游戏表示（CGR）[1-5]

蛋白质序列由20种不同的氨基酸组成[11]，即甘氨酸（G）、丙氨酸（A）、缬氨酸（V）、异亮氨酸（I）、亮氨酸（L）、苯丙氨酸（F）、脯氨酸（P）、甲硫氨酸（M）、色氨酸（W）、半胱氨酸（C）、丝氨酸（S）、苏氨酸（T）、天冬酰胺（N）、谷氨酸（E）、酪氨酸（Y）、组氨酸（H）、天冬氨酸（D）、谷酰胺（Q）、赖氨酸（K）和精氨酸（R）.根据detailed-HP模型[5，7，12-13]，可以把以上20种氨基酸分成4类：无极性氨基酸（A、I、L、M、F、P、W和V），负极性氨基酸（D和E），正极性氨基酸（R、H和K）和不带电氨基酸（N、C、Q、G、S、T和Y）.对一条长度为l的蛋白质序列s=s1s2…sl，其中si是20种氨基酸中的某一种，i=1，2，…，l，定义：这样就把蛋白质的氨基酸序列转换成了一条字符序列X（s）=a1a2…al，其中ai∈{0，1，2，3}.根据Jeffrey[1]的定义，一条蛋白质序列s的混沌游戏表示规则如下：先在平面上作一正方形[0，1]×[0，1]，以其4个顶点分别代表4个字符0、1、2和3，然后进行打点，第一点打在正方形中心与序列X（s）第一个字符对应顶点的中点，第i（i≥2）点打在第i-1点与序列X（s）第i个字符对应顶点的中点，直到在正方形中作出序列X（s）最后一个字符对应的点，这样得到的图像称为蛋白质序列s的混沌游戏表示CGR.

1.2 混沌游戏表示测度[5，8，10，12]

根据蛋白质序列混沌游戏表示的作法可知，序列X（s）与其CGR之间具有一一对应关系，即不同的蛋白质序列对应着不同的混沌游戏表示.为了进一步讨论的需要，引入蛋白质序列的混沌游戏表示的测度这一概念，对给定的蛋白质序列，以如下方式来定义其CGR测度：μ（B）＝＃（B）/N，其中＃（B）表示该蛋白质序列CGR子集B中点的数目，N表示蛋白质序列的长度.为了便于讨论，将正方形[0，1]×[0，1]分割成2k×2k个小正方形网格，对每一种分割，取B为该分割中每一网格与蛋白质序列CGR的交集，则＃（B）就是该网格上CGR点的数目，这样我们得到2k×2k的测度矩阵.

1.3 递归迭代函数系统（RIFS）[2，5-10]

在完备距离空间X上，一个由压缩映射集S＝{S1，…，SN}和与其对应的概率集P＝（pij）（其中构成的系统（S，P），任取起始点A0，按如下的迭代过程产生随机点列：An+1=Sσn（An）（n＝0，1，2，…），其中σn在集合{1，2，…，N}中取值且P（σn+1＝i）=pσni，i=1，…，N，则称（S，P）为递归迭代函数系统.

在本文中，我们取X=[0，1]×[0,1]，N=4，压缩映射为：1，2，3，4，即：

递归迭代函数系统的一个主要结论是：存在唯一不变测度且其支撑集为递归迭代函数系统的吸引子.由于需要用递归迭代函数系统的吸引子来逼近蛋白质序列的混沌游戏表示，所以为了得到给定的蛋白质序列对应的RIFS的吸引子，我们根据已知蛋白质序列混沌游戏表示的测度，用矩方法来估计递归迭代函数系统中的未知参数pij.如果μ′与A分别是RIFS的不变测度与吸引子，则μ′的矩为：

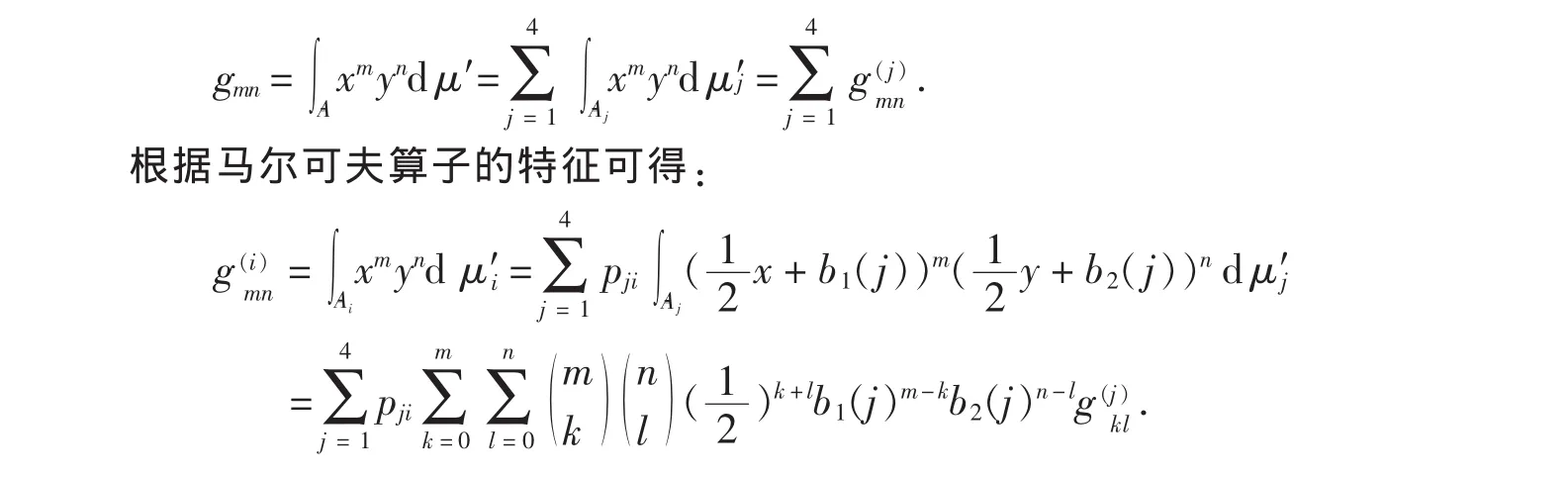
记Gmn为蛋白质序列的混沌游戏表示测度μ的各阶矩，通过解优化问题Gmn）2可得参数pij的估计值，根据其估计值可以产生上述RIFS吸引子A，记χB为吸引子A的子集B的特征函数，根据RIFS遍历理论可知其不变测度为：μ′（B）＝这样就可以计算出与上述蛋白质序列混沌游戏表示的测度矩阵同样大小的不变测度矩阵，然后根据它们的差异程度来判别RIFS的吸引子逼近蛋白质序列CGR的好坏.

1.4 CGR模拟效果判断[2，5-6，10]

1.4.1 相对标准误差

为了说明不变测度对原始测度的模拟效果，引入相对标准误差：e=e1/e2，其中e1=为原始测度矩阵的元素，yij为模拟测度矩阵的元素，若e＜1，则说明拟合得比较好，如果e＜0.1，则拟合的效果更好[2].

1.4.2 测度累积行走

测度累积行走定义如下：其中fi是将测度矩阵的k×k网格所有行扩展为一行后第i个网格的密度值，是网格上所有密度值的平均值.

2 结果与分析

数据库Genebank（ftp://ncbi.nlm.nih.gov/genbank/genomes）中有大量的蛋白质序列，从中随机下载了20种细菌（见表1）的蛋白质序列.以细菌Thevo（Thermoplasma volcanium，火山热原体，广古生菌（Euryarchaeota））为例，根据1.1节中的方法，图1是Thevo蛋白质序列的混沌游戏表示，该图呈现出明显的分形特征.根据1.2节中的方法，图2是k=7时Thevo蛋白质序列混沌游戏表示的测度图.基于1.3节中的理论，通过计算得到参数pij的估计为:

根据概率矩阵P4×4得到了对应的k=7时递归迭代函数系统的吸引子图3及不变测度图4.对于Thevo而言，根据1.4.1节的方法，计算得到e=0.130 8，根据1.4.2节的方法，图5给出了k=7时Thevo的CGR测度行走表示及其模拟的比较图，表明用递归迭代函数系统能很好地模拟Thevo的蛋白质序列CGR.为了对模拟结果进一步优化，我们考虑两个问题：第一，迭代次数是否影响迭代结果？第二，k的不同取值是否影响迭代效果？在文献［2，5］中，都是选用k=7来进行研究.实验证实迭代次数并不影响迭代结果，而k的不同取值可以影响迭代效果.以Thevo为例，图6～8分别是k=8时Thero的CGR测度，RIFS吸引子及RIFS模拟CGR的不变测度，由图1和图3、图2和图4的对比结果与图1和图7、图6和图8的对比结果可以直观地看出，k=8时的模拟效果明显优于k=7时的模拟效果，图5和图9分别表示k=7和8时，Thevo的CGR测度行走表示及其模拟的比较图，也很好地证实了上述结论.此时，参数pij的估计为：

而且从表1可以看出，对Thevo而言，k=8时有最好的模拟效果.之后随机选取了20种不同细菌进行实验发现，当k取不同的值时，其模拟效果是不同的，可以选取不同的k值使其模拟效果达到最优（见表1）.其缺点就是过程相对麻烦，需要进行反复的实验去寻找适合的k值.

图1 Thevo的CGR

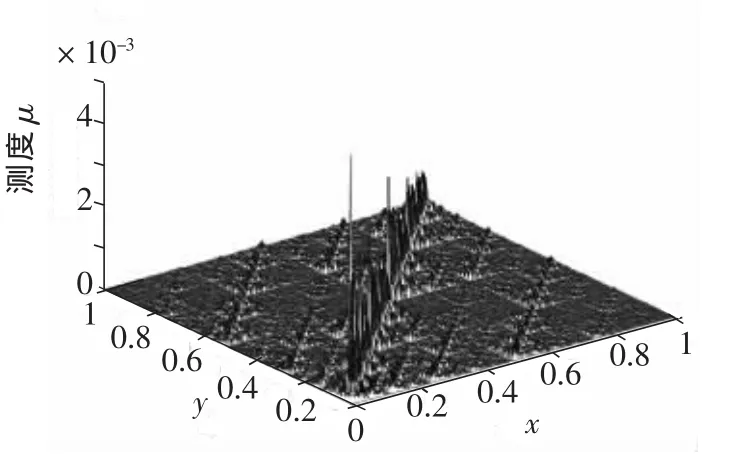
图2 k=7时Thevo的CGR测度

图3 k=7时Thevo的RIFS吸引子

图4 k=7时Thevo的RIFS模拟CGR不变测度

表1 不同k值时RIFS对20种细菌的CGR模拟结果

细菌名称（简写）蛋白质序列长度相对标准误差k=7k=8k=9k=10k=11k=12Cloab1 123 6040.189 50.180 50.092 30.099 20.099 60.099 8 lo640 5460.052 70.037 70.039 10.041 10.043 50.044 8Borbu283 5960.200 80.167 80.152 70.101 40.108 10.115 3Brume950 1280.038 20.036 00.027 30.025 90.026 90.027 8Camje508 8370.080 20.083 80.025 70.026 00.026 70.027 2Caucr1 209 2280.025 90.024 20.015 80.016 20.017 20.018 1Chlmu321 0650.118 30.113 80.092 40.098 10.098 70.113 2ChlpnAYerpek1 273 9040.068 90.058 00.055 10.057 50.058 60.060 5Wigbr201 6721.103 51.116 90.867 70.932 00.961 20.964 0Thevo450 1070.130 80.050 30.053 60.055 20.057 20.063 5Mycpe400 8000.325 30.221 70.230 20.235 20.241 20.251 1Urepa228 2390.405 80.330 30.248 10.262 80.268 90.271 3Bachd1 188 4480.048 70.046 60.034 60.036 70.037 20.038 2Bacsu1 218 6160.068 60.041 80.042 30.043 30.045 10.048 1Bif 364 0780.104 40.098 20.061 90.064 60.074 50.086 7

3 结语

用分形方法中的递归迭代函数系统对基于detailed-HP模型的蛋白质序列可视化方法——混沌游戏表示作了逼近，分析发现用递归迭代函数系统来逼近蛋白质序列的混沌游戏表示时有好的效果，且其模拟结果可以进一步优化，为更准确地进行物种亲缘关系的分析提供一种新的方法.

[1] Jeffrey H J.Chaos game representation of gene structure[J].Nucleic Acids Res，1990（18）：2 163-2 170.

[2] 肖前军.递归迭代函数系统对基于detailed-HP模型的蛋白质序列的混沌游戏表示的模拟[J].湘潭师范学院学报（自然科学版），2008，30（1）：14-17.

[3] 肯尼思·法尔科内.分形几何中的技巧[M].曾文曲，王向阳，陆夷，等，译.沈阳：东北大学出版社，1999.

[4] 肯尼思·法尔科内.分形几何——数学基础及其应用[M].曾文曲，王向阳，陆夷，等，译.沈阳：东北大学出版社，2001.

[5] 肖前军.功能蛋白质序列的混沌游戏表示及其递归迭代函数系统模拟[D].湘潭：湘潭大学数学与计算科学学院，2008.

[6] Lau K S，Anh V V，Yu Z G.Recognition of an organism from fragments of its complete genomes[J].Physical Review E，2002（66）：0319101-9.

[7] 喻祖国，Vo Anh，刘家成.迭代函数系统模型在生物序列分析中的应用[J].湘潭大学（自然科学学报），2003（9）：131-139.

[8] Yu Z G,Anh V V,Wanliss J A，et al.Chaos game representation of the dst index and prediction of geomagnetic storm events[J].Chaos,Solitons and Fractals,2007（31）：736-746.

[9] Vrscay E R.Fractal geometry and analysis,chapter iterated function systems：theory，applicationsand the inverse problem[M].Dorsrecht：Kluwer，1991:405-468.

[10] Yu Z G,Shi L，Xiao Q J，et al.Simulation for chaos game representation of genomes by recurrent iterated function systems[J].J Biomedical Science and Engineering,2008（1）:44-51.

[11] 孙啸，陆祖宏，谢建明，等.生物信息学基础[M].北京：清华大学出版社,2005.

[12] Yu Z G,Anh V V,Lau K S.Chaos game representation of protein sequences based on the detailed HP model and their multifractal and correlation analyses[J].Journal of Theoretical Biology,2004（226）：341-348.

[13] Yu Z G,Anh V V,Lau K S.Fractal analysis of measure representation of large proteins based on the detailed HP model[J].Physica A:Statistical and Theoretical Physics,2004（337）:171-184.

Optimization of Simulation for Chaos Game Representation of Protein Sequence

XIAO Qian-jun，ZHOU Jin-yu，DENG Zong-gang

（Hunan Vocational College of Science and Technology,Xiangtan 411104,Hunan,China）

A fractal pattern is apparent in visual representation of a protein sequence：Chaos Game Representation（CGR）.According to the mechanism of fractal forming，Chaos Game Representation（CGR）of protein sequences can be simulated by Recurrent Iterated Function System（RIFS）.In experiments，a close approximation of CGR is obtained by the method.The results of simulation can be further optimized and the phylogenetic tree can be correctly worked out.

iterated function system；chaos game representation；simulation；protein sequence；optimization

O 29；O 811.4；Q 516

A

1001-4217（2010）01-0035-07

2009-06-24

肖前军（1978-），男，湖南湘潭人，讲师.研究方向：分形几何与生物信息学.E-mail：xqjxt@126.com

2008年湖南省教育厅项目（08C882）