中子衍射应力分析谱仪的模拟和优化

陈 华 黄朝强 孙光爱 陈 波

(中国工程物理研究院核物理与化学研究所 绵阳 621900)

在加工制造和/或载荷服役过程中，材料或部件会产生残余应力，影响它们的稳定性、抗疲劳强度、静强度等使用性能[1]。中子衍射法是在附加外场(温度、压力等)下测量工件内部应力场的唯一非破坏性方法。国外众多中子散射实验室纷纷建立中子衍射应力分析谱仪，开展残余应力测量工作，如澳大利亚核科学技术组织(ANSTO)的KOWARI[2]、法国劳厄-郎之万研究所(ILL)的 SALSA[3]等。随着谱仪性能的提高，其结构越来越复杂，多用蒙特卡罗模拟方法进行此类谱仪的设计优化。McStas[4,5]是丹麦RISΦ国家实验室研制的中子散射装置蒙特卡罗射线追踪模拟的软件平台，本文选用McStas1.12作模拟计算工具。郭立平等[6,7]对中子应力谱仪不同 Ge单色器进行模拟，获得最佳组合Ge(311)或Ge(511)。我院中子应力谱仪概念设计选择 Cu作垂直聚焦单色器，为验证其合理性，本文对Cu和Ge常用晶体单色器进行模拟与比较。此外还对导管、准直器等中子部件参数进行了优化设计，为谱仪设计方案及实验提供必要的参考数据。

1 中子衍射应力分析谱仪的总体布局

中子衍射应力分析谱仪布局如图1所示。由于安放空间限制，谱仪距离水平孔道出口较远。为屏蔽及减小中子强度损失，在水平孔道后设置一段中子直导管。中子束从水平孔道引出后，经导管、第一准直器入射到单色器上，单色器将满足布喇格条件的单色中子束反射出来，经第二准直器和限束孔入射到样品上，样品产生的衍射束经限束孔、第三准直器后被探测器记录。准直器水平发散度可调。单色器起飞角2θM在60°–120°间连续变化，以选择合适的中子波长和谱仪分辨。下文用 McStas 1.12确定中子导管长度l、单色器单晶条数N、单色器聚焦曲率半径R、第一、二、三准直器水平发散度ai，研究不同光路下谱仪的强度和分辨。

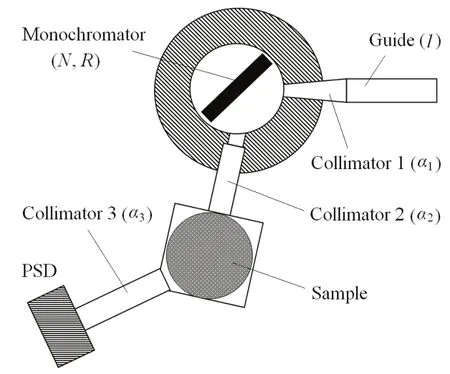
图1 中子衍射应力分析谱仪布局示意图Fig.1 Schematic illustration of residual stress neutron diffractometer.

2 中子导管

假定热中子孔道入口处中子能谱服从麦克斯韦分布，使用Source_Maxwell_3模块模拟中子源。热中子温度 T1=320 K，积分注量率 I1=9.87×1012cm–2·s–1·ster–1，则模拟能谱如图 2。

McStas组件库未直接提供热中子孔道模型。简化为两个开口110 mm(H)×60 mm(W)、间距4.05 m的限束孔，即用两个 slit模块替代。使用straight_guide模块模拟直导管。根据谱仪安放空间，直导管长度l优化范围设4–7 m，扫描点步距为0.5 m；导管横截面尺寸同水平孔道；超镜临界角增大因子m为2；抽样中子数为108。导管出口中子强度随导管长度l增加而减小，l=7 m的强度是l=4 m的 75.4%(图 3)。

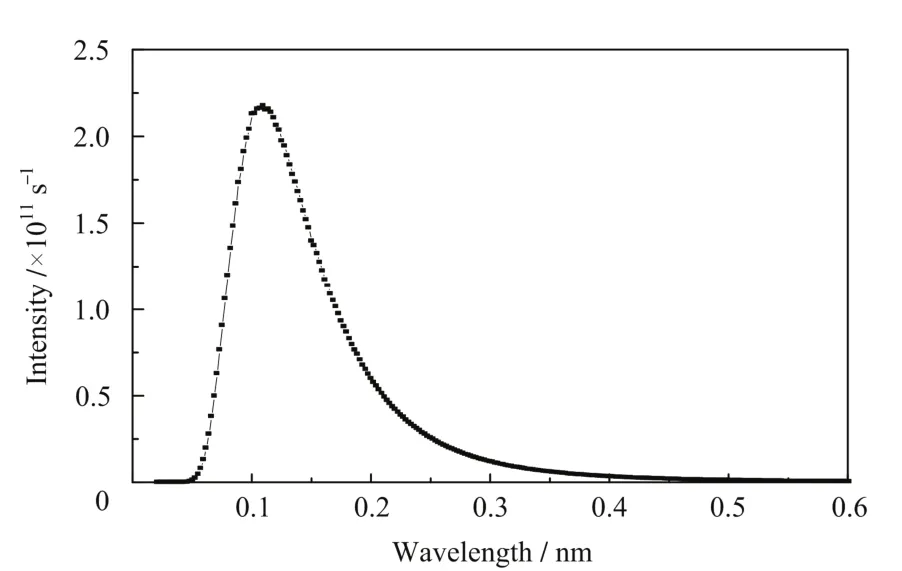
图2 热中子孔道入口中子能谱图Fig.2 Neutron spectrum at thermal channel exit.

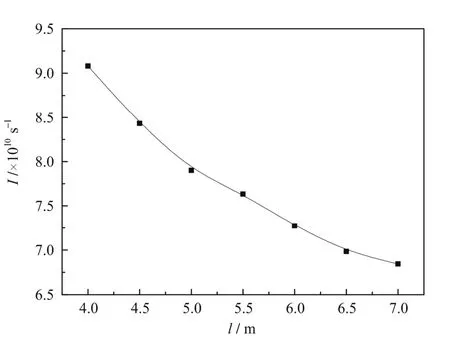
图3 不同导管长度对应导管出口中子束强度Fig.3 Neutron intensity at guide exit for different l.

3 单色器

单色器是中子衍射应力分析谱仪的核心部件之一，对谱仪的分辨率和注量率有重要影响。相对平板单色器，垂直聚焦单色器可提高样品处的中子注量率 2–5 倍[1]。

本文单色器由 15条单晶片纵向排列形成圆柱面。相邻单晶片间留0.5 mm间隙以便转动。通过调节相邻单晶片倾角ω来调节单色器曲率半径R，使入射中子束刚好汇聚于取样体积处(见图4)。

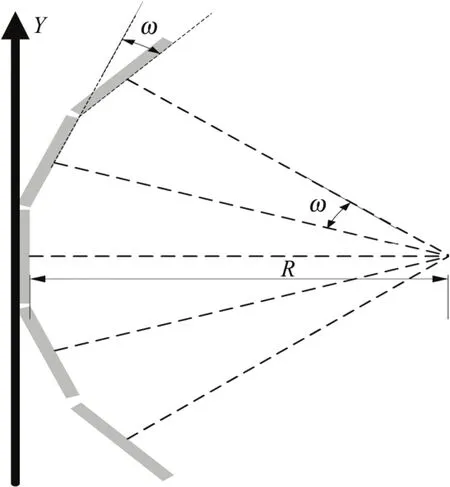
图4 垂直聚焦单色器侧视示意图Fig.4 Side view of the vertical bent monochromator.

单色器高 150 mm，所需宽度随起飞角变化，镶嵌度 30′且各向同性。整个单色器可绕垂直轴转动，以获得一定波长范围内的单色中子。单色器可在多种单晶片间切换，满足不同的注量率和分辨率要求。

使用弯曲单色器(curved monochromator)模块模拟垂直聚焦单色器。通过NOP程序计算得到单色器的峰反射率R0[8]。为使峰反射率达到最大值，厚度均设为1 cm[9]。

3.1 单晶条数对谱仪性能的影响

单色器高度和聚焦曲率半径确定后，纵向单晶条数会影响单色器的聚焦效果。条数越少，形成的凹面越粗糙，汇聚效果越差；条数越多，通过单晶条间隙漏出的中子越多，对单色器组装工艺和机械装置精度的要求越高。为合理设计单晶条数，以Cu(220)为反射面模拟计算了不同单晶条数对应的注量率，结果如图5所示，样品处中子注量率随单晶条数增加而提高，单晶条13块时比5块的中子注量率增加约 16%，当单晶条数超过13块后注量率有略微下降，变化趋势与分析符合。

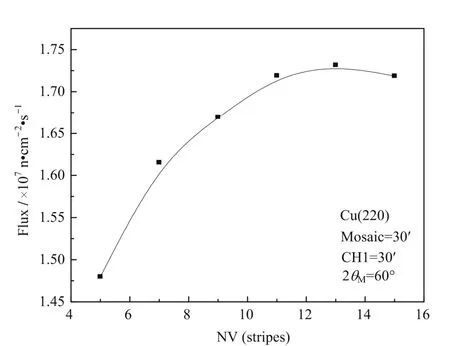
图5 单色器单晶条数对样品处中子注量率的影响Fig.5 Influence of number of monochromator stripes on neutron flux at the sample position.

3.2 聚焦曲率半径对中子注量率的影响

当垂直方向产生聚焦效果时，探测器计数达到最大，倾角即为聚焦倾角ω，对应的曲率半径为聚焦曲率半径R。相邻单晶条间的倾角ω与单色器的曲率半径R、单晶条高度h的关系如下：

聚焦曲率半径R通过式(2)[10]计算得到：

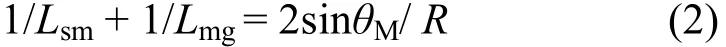
式中，Lsm为中子源到单色器距离，Lmg为单色器到聚焦点距离，θM为单色器布喇格角。

表1是单色器为Cu(110)、样品距离单色器1.5 m和1.9 m时聚焦倾角模拟值ωs和理论计算值ωt的比较。模拟时在样品位置放置截面尺寸为 8 mm(W)×8 mm(H)的虚拟探测器来记录中子积分强度。

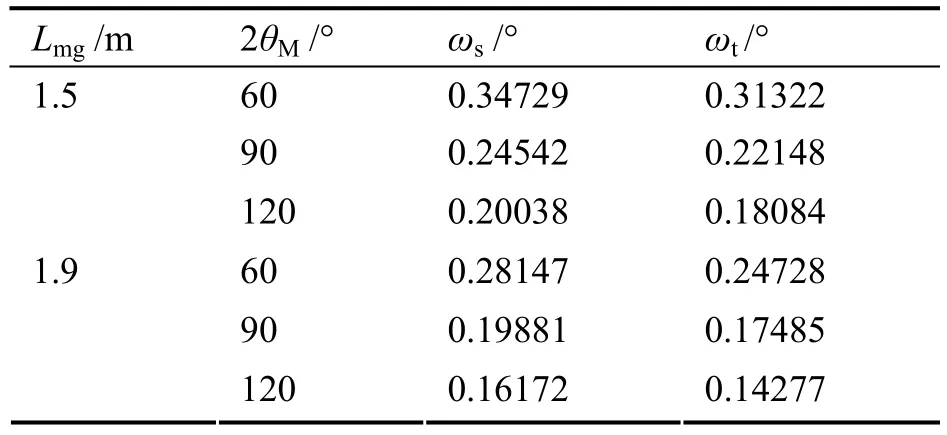
表1 聚焦倾角模拟值ωs和理论计算值ωt的比较Table 1 Comparison between ωs and ωt.

表1结果显示，ωs略大于ωt。文献[4]认为导致偏差是因为式(2)假定中子源为点源、将单色器视为凹面镜的前提下做的近似处理；解析计算忽略了第一准直器的限制作用，Lsm比实际源距大，认为聚焦成像为理想的点，而模拟计算考虑了聚焦束的实际高度，因此模拟计算值ωs更可信。

为实现垂直聚焦，单晶条倾角调整必须满足一定精度。由图6计算可知，为使中子注量率达到最大值60%以上，单晶条倾角精度必须控制在0.1°范围内。

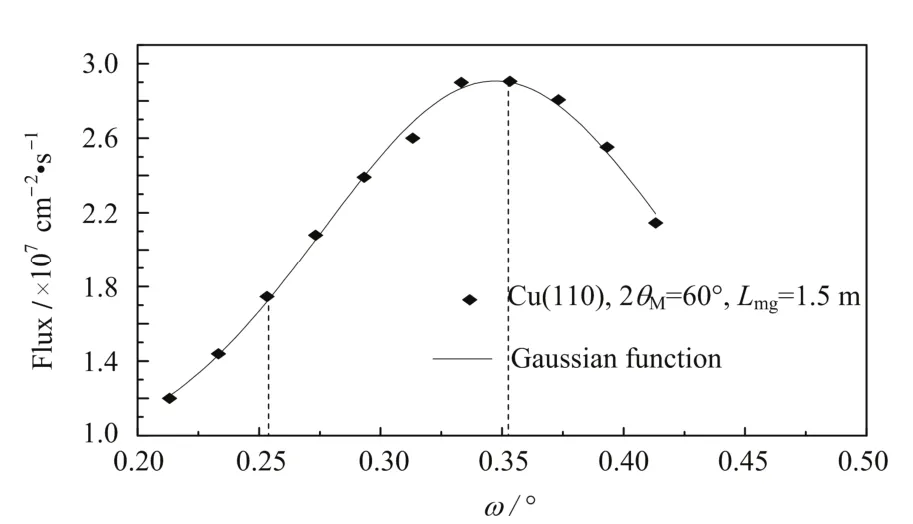
图6 样品处中子注量率随单晶条倾角变化情况Fig.6 Neutron fluxes at the sample position for different tilting angles of the crystal stripes.

3.3 几种单色器计算结果比较

模拟计算Cu和Ge各晶面在样品处获得单色中子注量率和波长分辨率。设第一准直器水平发散为30′，单色器镶嵌度为20′，起飞角60°，表2是各晶面在0.1–0.2 nm间获得的单色中子束，其中Cu(220)获得最大中子注量率，约是Ge(511)的3.6倍；Cu(222)获得最佳波长分辨率，半高宽约是 Cu(002)的36.2%。

表2 单色器采用不同晶面时样品处中子注量率和波长分辨率Table 2 Neutron fluxes and resolutions at the sample position with different monochromators.

4 准直器

样品衍射峰的半高宽 FWHM 和强度与谱仪准直系统角度发散及晶体镶嵌度有关。但分辨率的有限提高是以中子束强度的显著损失为代价的。高分辨和高强度是中子衍射应力分析谱仪必须同时具备的指标，因此需要根据具体光路对准直系统作优化选取。

添加标准α-Fe多晶样品，获得样品在无应变下的(211)模拟衍射峰，取样体积为 8 mm×8 mm×8 mm。单色器反射面为 Cu(220)，镶嵌度 20′，起飞角81.36°，中子波长为0.166623 nm，样品距离单色器1.9 m，探测器距离样品1 m。采用高斯峰形对衍射峰拟合。文献[11]定义品质因子FoM来表征强度和分辨率的均衡性。

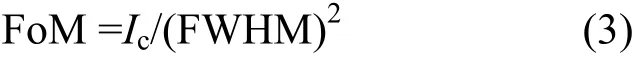
式中，Ic为衍射峰积分强度，FWHM为衍射峰半高宽。

图7a–7c分别是第一准直器水平发散α1、第二准直器水平发散α2、第三准直器水平发散α3对FoM的影响。由图7a，随α1递增FoM有起伏的变化。第一准直器为自然发散时，FoM约为5.6；α1为20′时，FoM=18.4。设置第一准直器水平发散度明显能够平衡强度和分辨率。由图7b，FoM 随α2单调上升。无第二准直器组的FoM最大值18.4约为有第二准直器组的FoM最小值4.0的4.9倍。由图7c，FoM随α3单调上升。无第三准直器组的FoM最大值18.4为有第三准直器组的FoM最小值8.7的2.1倍。另外α1较小时，第三准直器改善分辨率的作用不明显，例如当 α1=10′、α3=10′时，相对于无第三准直器FWHM仅减小了1.4874′；而α1较大时，第三准直器改善效果显著，例如当α1=30′、α3=10′时，相对于无第三准直器FWHM减小了10.7448′。

表3是最小FoM、最佳分辨、最大强度、最大FoM对应的准直系统配置。

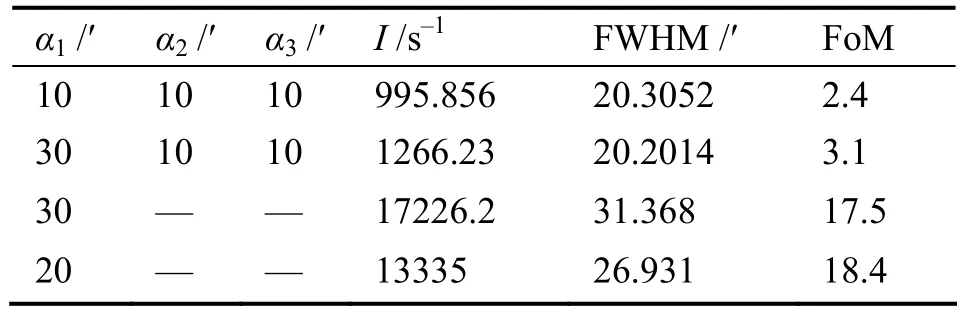
表3 四种准直器方案Table 3 Four collimation schemes.

5 结论

本文用蒙特卡罗程序 McStas对中子衍射应力分析谱仪的导管、单色器和准直系统进行模拟计算，为谱仪的设计提供参考数据。导管出口中子强度随导管长度l增加而减小，l取7 m时的强度是4 m时的75.4%。垂直聚焦条件下，当单色器总高度为150 mm、相邻晶条间隙取0.5 mm时，单晶数设置13条为最优。单晶条倾角精度会影响垂直聚焦效果，要使样品处注量率达到最大值60%以上，精度应好于0.1°。谱仪其它参数相同条件下，Cu和Ge常用晶面中Cu(220)获得的中子注量率最大，Cu(222)获得的波长分辨率最佳。最后考察了准直器水平发散度对品质因子的影响，得到最小FoM、最佳分辨、最大强度、最大FoM对应的准直系统配置。

1 丁大钊, 叶春堂, 赵志祥, 等. 中子物理学-原理、方法与应用. 原子能出版社, 2001. 753 DING Dazhao, YE Chuntang, ZHAO Zhixiang, et al.Neutron physics-principal, methods and application.Atomic Energy Press, 2001. 753

2 Kirstein O, Brule A, Nguyen H, et al. Kowari-The residual stress diffractometer for engineering applications at OPAL. International Conference on Stress Evaluation Using Neutrons and Synchrotron Radiation. 2007, 09:24–26

3 Pirling T, Bruno G, Withers P. Mater Sci Eng A, 2006,437(1): 139–144

4 Lefmann K, Nielsen K. Neutron News, 1999, 10(3): 20

5 Willendrup P, Farhi E, Lefmann K. Physica B, 2004, 350:735

6 郭立平, 李际周, 孙 凯, 等. 原子能科学技术, 2008,42(1): 74–75 GUO Liping, LI Jizhou, SUN Kai, et al. At Energy Sci Technol, 2008, 42(1): 74–75

7 郭立平, 李际周. 核技术, 2005, 28(3): 231–235 GUO Liping, LI Jizhou. Nucl Tech, 2005, 28(3): 231–235

8 Alianelli L, Sanchez M, Felici R. Physica B, 2004, 350:e730–e741

9 Freund A K. Nucl Instrum Methods in Phys Res, 1985,A238: 570–571

10 Riste T. Nucl Instrum Methods, 1970, 86(1): 1–4

11 Cser L, Rosta L, Grosz T. Residual Stress Diffractometer Introductory, 2007, 21