pk元域上的二次方程根的判定

孙宗明

(泰山学院数学与系统科学学院,山东泰安 271021)

pk元域上的二次方程根的判定

孙宗明

(泰山学院数学与系统科学学院,山东泰安 271021)

本文中,F是一个pk元域,0表示F的零元,e表示F的单位元.设方程ax2+bx+c=0(a≠0)是F上的一个二次方程.利用扩域的理论,讨论它的根,完整地给出了它在F中的根的状况:两个不同的根、两个相同的根、没有根,确定了有根的必要充分条件,定义了根的判别式.同时,研究了另外两类相关的方程.

pk元域;二次方程;根的判定;根的判别式

本文中,F是pk元域,0表示F的零元,e表示F的单位元.笔者于1980年写成的[1]于1983年发表;此后,上海交通大学沈灏先生来信给笔者,讨论[1]中所遗留的p=2的有关问题,至1984年,沈灏先生来信告诉笔者,他的学生完整地解决了p=2的情况,就是于1986年发表的[2];笔者利用[1]与[2]的有关结果,于1984年完成[3],并于1987年发表.[1]与[2]所得的结论与实数域上的二次方程的结论极其相似,但是,在pk元域上解决问题,却有相当的困难.本文利用扩域的理论,统一且自然地讨论F上的二次方程,并给出根的判别式的概念.同时,研究了F的单超越扩域E上的二次方程,提出了有关的问题.

1 若干引理

引理1.1 设域K的特征数为p,而w为非负整数,则对于任意的a1,a2,…,an∈K,有

证明 参见[4]的4.2,此处从略.

引理1.2 设w为非负整数,

证明 参见[4]的4.9,此处从略.

引理1.4 对于任意的d∈F成立

因此,结论成立.证完.

定义1.5 F上的pk-1次多项式

称为F的迹多项式.

引理1.6 对于∀d∈F,成立

证明 由定义1.5,得

从而,由引理1.1及引理1.4,得

因此,引理得证.证完.

2 p≥3的情况

引理2.1 设有F上的二次方程

则有F上的二次方程

其中

并且,(1)与(2)同解.

证明 记4a=(4e)a,则有

并且,(1)在F中有根x=x0当且仅当(2)在F中有根y=y0=2ax0+b,从而,引理得证.证完.

这样,(1)的研究就转化为x2=d的研究,而d=0时x2=d有二重根0,下面研究d≠0的情况.

定理2.2 F上的方程x2=d(d≠0)在F中有根⇔dm=e,其中m=(pk-1)/2.

上面的△=b2-4ac,与实系数二次方程根的判别式相同.但是,它还不能作为(1)的根的判别式,因为△还不能直接区分出根的状况.当△≠0时,由引理1.3可知△pk-1=e,而m=(pk-1)/2,即2m=pk-1,则有

从而得到

此外,△m=0当且仅当△=0.这就得出了下面的定义.

定义2.3 △m称为(1)的根的判别式.

总结上面的讨论,得到下面的定理.

定理2.4 设△=b2-4ac,m=(pk-1)/2,则(1)在F中的根的状况是:

在F中有两个不同的根⇔△m=e;

在F中有两个相同的根⇔△m=0;

在F中没有根⇔△m=-e.

证明 这是一个分断式命题,只须证明一方即可,现在证明⇐.

当△m=e时,由定理2.2,有x0使x20=△.从而就有

当△m=0时,必有△=0,从而(2ax+b)2=0,于是得到

当△m=-e时,由定理2.2,在F上没有根.证完.

当△m=-e时,ax2+bx+c是F上的二次不可约多项式,取其一根α,则F(α)是一个p2k元域.此时

从而,(1)在F(α)中有两个不同的根.这样,就得到下面的结论.

结论2.5 当△m=-e时,(1)在F的某个单扩域F(α)中有两个不同的根.

关于定理2.2中的方程x2=d,可以类似地推广到xn=d(d≠0),其中,n为正整数,有下面的结论.

结论2.6 F中的方程xn=d(d≠0)在F中有根当且仅当du=e,其中

3 p=2的情况

当b=0时,方程(1)的根,在[1]中已解决,实际上,有下面的

结论3.1 2k元域上的方程(1)有两个相同的根⇔b=0.

证明 ⇒设(1)有两个相同的根x1=x2,则

⇐当b=0时,(1)可以写为x2=a-1c.由引理1.2得,有x0∈F,使=a-1c.从而,(1)有两个相同的根x1=x2=x0.实际上,x0=(a-1c)2k-1.证完.

下面讨论b≠0的情况.

引理3.2 设有2k元域F上的二次方程

且b≠0,则有F上的方程

使(1)与(3)同解.

证明 对于(1),设x=a-1by,则

从而,(1)有根x=x0当且仅当(3)有根y=y0=ab-1x0,因此,(1)与(3)同解.证完.

这样,(1)的研究就转化为(3)的研究,而对于(3)可得,(3)在F中有根当且仅当有元素y∈F,使得y2+y=ab-2c.于是,就需要研究F中形状为y2+y的元素.

引理3.3 集合

是迹多项式Tk(x)的所有根的集合.

证明 因为

即y-z为u2+u=0的一个根0或e,从而两个元素y与y+e对应同一个元素y2+y,从而,{y2+y|y∈F}是2k-1元集合.

又因为

所以,y2+y是Tk(x)的根.而Tk(x)是2k-1次的,因此,结论成立.证完.

定理3.4 方程(3)在F中有根⇔Tk(Ω)=0,其中Ω=acb-2,并且,此时有两个不同的根.

证明 ⇒设y=y0是(3)的一个根,则

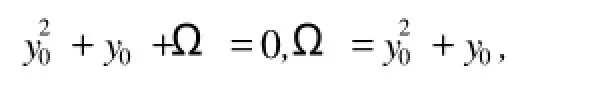
由引理3.3得,Tk(Ω)=0.

⇐若Tk(Ω)=0,则Ω为Tk(x)的根.由引理3.3得,必有y0∈F,使得

所以,(3)在F中有根.此时,(3)有两个不同的根y1=y0,y2=y0+e.因此,定理得证.证完.

根据上面的讨论,很自然地引出下面的

定义3.5 称Tk(Ω)为2k元域F上的方程(1)的根的判别式.

容易证明下面的

结论3.6 Tk(Ω)=e或0.

综合上面的结论3.1与定理3.4及结论3.6,得到下面的定理.

定理3.7 2k元域F上的方程(1)在F中的状况是:

有两个相同的根⇔b=0;

有两个不同的根⇔Tk(Ω)=0;

没有根⇔Tk(Ω)=e.

定理3.7与定理2.4一样,也是一个分断式命题.

当Tk(Ω)=e时,y2+y+Ω是F上的不可约多项式.取其一根α,则F(α)为22k元域,并且

从而,(3)在F(α)中有两个不同的根.这就得到下面的结论.

结论3.8 当Tk(Ω)=e时,(3)在F的某个单扩域F(α)中有两个不同的根.

4 一类2ps次方程

[3]中研究了F上的一类2ps次方程,利用第2款与第3款中的结论,完整地给出了其根的状况,就是下面的两个定理.

定理4.1 设有F上的一类2ps次方程

其中p≥3,s为非负整数,记

则(4)在F中的根的状况是:

在F中有两组不同的ps重根⇔△m=e;

在F中有2ps重根⇔△m=0;

在F中没有根⇔△m=-e.

很自然地,称△=b2-4psac是(4)在p≥3时的根的判别式.

定理4.2 设有F上的一类2ps次方程(4),其中p=2,s为非负整数,则(4)在F中的根的状况是:

在F中有两组不同的ps重根⇔Tk(Ω)=0;

在F中有2ps重根⇔b=0;

在F中没有根⇔Tk(Ω)=e.

很自然地,称Tk(Ω)是(4)在p=2时根的判别式.

上面的两个定理的证明参见[3],此处均从略.

类似地,可以讨论F上的方程

5 F的单超越扩域上的二次方程

设E是F的单超越扩域,由[4]知,F上的未定元的有理函数域F(x)与E同构,从而就记E= F(x).

本款中,F的元素用a,b,c,…表示,E的元素用A,B,C,…表示;为方便,将单位元e记为1.

本款研究E上的二次方程

本款中,仅列出结论,相应的证明参见[5],此处均从略.

定义5.1 设A∈E,n为正整数,若存在B∈E,使得Bn=A,则称A是E的一个n方元素.

引理5.2 E中的任一个非零元素A均可以写为A=f(x)/g(x),其中f(x),g(x)∈F[x],且(f(x),g(x))=1,f(x)或g(x)的首相系数为1.

定理5.3 设A∈E,A≠0,则A是n方元⇔存在f1(x),g1(x)∈F[x],并且(f1(x),g1(x))=1,f1(x)的首项系数为1,满足A=(x)/(x).

推论5.4 设A≠0,A∈F[x],则A是E的p方元素⇔A是F[x]中xp的多项式.

定理5.5 设n为正整数,A≠0,A∈E,则E上的方程yn=A在E中有根⇔存在f1(x),g1(x)∈F[x], (f1(x),g1(x))=1,f1(x)的首项系数为1,使得A=(x)/(x).

定理5.6 设域E的特征数p≥3,Ay2+B y+C=0(A≠0)是E上的二次方程,△=B2-4AC,则(6)在E中的根的状况是:

在E中有两个相同的根⇔△=0;

在E中有两个不同的根⇔△≠0且△是平方元素;

在E中没有根⇔△≠0且△不是平方元素.

引理5.7 设E特征数p=2,而

是E上的方程,其中f(x),g(x)∈F[x],(f(x),g(x))=1,g(x)的首项系数为1,则(7)在E上有两个不同的根⇔存在f1(x),g1(x)∈f[x],(f1(x),g1(x))=1,g1(x)的首项系数为1,并且

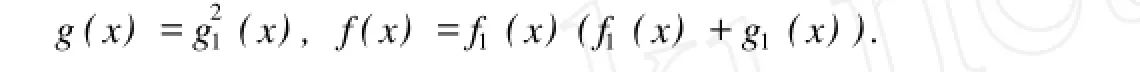
定理5.8 设域E的特征数p=2,Ay2+B y+C=0(A≠0)是E上的二次方程,则(6)在E中的根的状况是:

在E中有两个相同的根⇔B=0且A-1C为平方元素;

在E中有两个不同的根⇔B≠0且存在f1(x),g1(x)∈f[x],(f1(x),g1(x))=1,g1(x)的首项系数为1,使得

在E中没有根⇔B=0且A-1C不为平方元素,或者,B≠0且对于任意f1(x),g1(x)∈F[x], (f1(x),g1(x))=1,g1(x)的首项系数为1,均有

6 结束语

上面讨论了pk元域上的二次方程的根的判别问题,并且列出了一类2ps次方程的根的结论,还列出了pk元域F的单超越扩域E上的二次方程的根的结论.

实际上,下列两方面的问题应该是本文的继续,准备另外撰文给以阐述.

问题6.1 三项方程.

作为方程(4)的自然的推广,有F上的如下的方程

其中q为任意素数,以及方程

其中n为任意正整数.笔者在[6]与[7]给出了方程(8)与(9)的根的状况.自然地,利用方程(6)的结论,可以讨论E上的方程

其中n为任意正整数,笔者也曾考虑了方程(10)的根的状况.

问题6.2 根的公式.

笔者在[8]中给出了2k元域上的一类二次方程的根的公式,随后,有同行继续研究了[8]中的遗留问题.这是对二次方程的更为精细的讨论.

不难看出,pk元域F及其有关的域上的二次方程的问题,其内容是相当丰富的,并且,可以从不同的角度进行不断的扩展,全面地总结这方面的相关资料,也将会得到科研思维的基本训练.

[1]孙宗明.pk(p≧3)元域上的二次方程的根的状况[J].数学的实践与认识,1983,(4):29-31(美国,M ath.Reviw s,1985(i): 11104).

[2]唐俊杰.有限域GF(2m)上的二次方程根的判定[J].数学的实践与认识,1986,(2):57-59.

[3]孙宗明.pk元域上的2pS次方程的根的状况[J].数学的实践与认识,1987,(1):43-45(美国,M ath.Reviw s,1988年索引, P1094).

[4]熊全淹.近世代数[M].上海:上海科学技术出版社,1978.

[5]孙宗明.pk元域F的单超越扩域E上的二次方程[J].河北师范大学学报,1992,(3):14-16.

[6]孙宗明.pk元域上的方程ax2q+bxq+c=0[J].内蒙古师范大学学报,1990,(1):22-26(美国,M ath.Reviw s,1992(h):11110).

[7]孙宗明.pk元域上的二项方程和三项方程根的状况[J].内蒙古师范大学学报,1991,(3):20-24(美国,M ath.Reviw s,1996(f): 12001).

[8]孙宗明.2k元域上的二次方程的根的公式[J].数学的实践与认识,2001,31(6):732-733(美国,M ath.Reviw s,2002年索引, P1924).

The Judgem en t of Rootsof Quadratic Equa tionsover a Field w ith pkElem en ts

SUN Zong-m ing
(Schoo lofM athem atics and System s Science,Taishan Universiy,Tai’an,271021,China)

In this paper,let F be a field w ith pkelem en ts,0 be the zero elem en tof F and e be the unit elem entof F.Let ax2+bx+c=0(a≠0)be an equation over F.U sing theory of extension field,the author discusses thisequation,comp letely gives its roots,that is,it has two distinct rootsor two sam e roots,and it has no roots.The autho r setsnecessary and sufficientconditions that the equation has roots,and defines judgem en t exp ression of roo ts.A t the sam e tim e,the au tho r stud ieso ther two c lassesof equations,too.

fie ld w ith pkelem ents;quad ratic equation;judgem ent of roots;judgem ent exp ression of roots

O153.4

A

1672-2590(2010)03-0008-07

2010-04-06

孙宗明(1945-),男,山东嘉祥人,泰山学院数学与系统科学学院教授.