(SiO2)n－(n≤7)团簇的密度泛函研究*

张岩陈雪风齐凯天李兵杨传路盛勇†

1)(四川大学材料科学与工程学院，成都610065)

2)(鲁东大学物理与电子工程学院，烟台264025)

(2009年9月16日收到;2009年10月12日收到修改稿)

(SiO2)n－(n≤7)团簇的密度泛函研究*

张岩1)†陈雪风1)齐凯天1)李兵1)杨传路2)盛勇1)††

1)(四川大学材料科学与工程学院，成都610065)

2)(鲁东大学物理与电子工程学院，烟台264025)

(2009年9月16日收到;2009年10月12日收到修改稿)

采用密度泛函理论中的广义梯度近似对(SiO2)n－(n≤7)负离子团簇的几何构型进行了优化，并对能量和频率进行了计算.通过对计算结果的分析发现，与近邻尺寸的团簇比较，(SiO2)4－团簇最低能量结构更加稳定; (SiO2)n－(n≥4)团簇的最低能量结构是以(SiO2)4－为基础结构，具有一定的生长规律.

二氧化硅，负离子团簇，密度泛函

PACC:3640，3640B，3120A

1. 引言

SiO2是科学技术领域的重要材料［1—3］，因此人们对SiO2的研究相对比较深入.近年来，团簇是实验和理论研究的热门课题［4—6］，研究者已对中性(SiO2)n团簇做过许多实验及理论方面的研究［7—17］.对SiO2分子层次的理论研究可以有助于对块体SiO2材料的进一步了解.Harkless等［7］用分子动力学模拟和经验相互作用势找出了(SiO2)n(n= 1—8)可能的稳定结构.Nayak等［8］在广义梯度近似(GGA)基础上用密度泛函理论(DFT)的Becke交换函数和Perdew-Wang的关联函数计算了(SiO2)n(n=1—6).Flikkema和Bromley［9，10］在B3LYP/6-31G(d)的计算水平上，对纳米尺寸的SiO2使用BH (basin hopping)全局优化［18］和新的拟合原子间作用势得到了(SiO2)n(n=6—12)的最低能量结构.理论和实验上得到的有关硅氧团簇结构和性质的数据表明，对于(SiO2)n，当n<7时，链状结构最稳定;当n≥7时，文献结论还未达到一致.(SiO2)n当分子团簇在得到一个电子时的能量及几何结构以及最稳定的基态结构也是该团簇结构研究的重要方面，而(SiO2)－n负离子团簇的研究目前国内外鲜有报道，Wang等［19，20］只是对直链状的(SiO2)－n(n≤ 4)的结构进行了一般性的研究.本文拟通过对(SiO2)n－(n≤7)负离子团簇的结构和稳定性的研究，以期更全面地了解SiO2小分子团簇的理论特性.

2. 计算方法

采用DFT下的GGA，用DMoL3软件包［21］对(SiO2)n－(n≤7)构型进行结构优化和电子性质计算.在GGA中，选择Perdew2Wang(PW91)交换关联泛函［22］，所有的计算均是在Fine网格下完成的，采用带极化的双数值原子基组(DNP)进行全电子计算，自洽过程以体系的能量和电荷密度分布是否收敛为依据，精度均优于10－6a.u.，梯度和位移的收敛精度优于2×10－3a.u./nm和5×10－4nm，能量的收敛精度优于10－5a.u..计算了几何构型、能量及频率.为了对所用计算方法进行标定，分别用PW91，B3LYP优化计算了(SiO2)n(n≤7)的结构和能量.以前许多研究已经表明B3LYP/6-31G对SiO2团簇的计算具有较高精度［8，11，12］.计算结果表明，对于(SiO2)n(n≤6)两种算法得出的基态结构相同，都是直链结构;当n=7时，由PW91/DNP得出的最低能量结构与Flikkema等［10］使用BH全局优化和新的拟合原子间势的计算结果相同，与B3LYP/6-31G计算得出的亚稳态结构相同.由图1可以看出，两种算法得出的结合能比较相近.综上可得PW91适用于中性(SiO2)n(n≤7)团簇的研究，于是我们认为PW91也适用于计算(SiO2)－n(n≤7)负离子团簇.

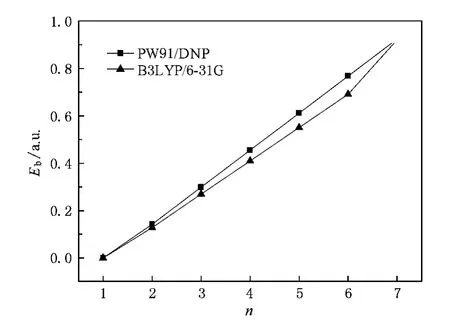
图1 两种计算方法得到的(SiO2)n(n≤7)中性团簇结合能的对比

3. 结果及讨论

3.1. 几何结构

在几何优化的基础上对频率进行了计算，把能量最低且振动频率为正值的结构确定为最低能量结构.图2给出了(SiO2)－n(n≤7)负离子团簇的最低能量结构.(SiO2)－相对于中性SiO2的D∞h结构，产生了一定的弯曲，构成键角为137°的线形结构，与Wang等［20］得出的键角140°的结构相近. (SiO2)2－同样也是尾端一个O原子弯曲，与中性(SiO2)2相比构型由D2h结构转变成了Cs结构. Wang等［20］认为这是由于多余的一个电子吸附到一个Si原子上，使它的杂化轨道由sp2转化成sp3，从而导致与它相连的终端O原子变形.(SiO2)－n(n≥3)负离子团簇的最低能量结构不再与中性SiO2团簇的基态结构相关.(SiO2)3－为Cs结构，相对于中性同样构型，其两个终端O原子所连接的键键长由0.1672nm下降到0.1537nm，其他键键长也都有相近程度的下降.(SiO2)4－是对称性为Cs的双六元环结构，左右两环呈镜面对称.(SiO2)5－为C1结构，不再具备对称性，其结构可认为是在(SiO2)4－的基础之上加上一个单位的SiO2得出.(SiO2)5－加上一个单位的SiO2则得出(SiO2)6－的最低能量结构，再加上一个单位的SiO2则得出(SiO2)7－的最低能量结构.综上可以看出，(SiO2)n－(n≤3)没有具体的生长规律;而(SiO2)n－(n≥4)的负离子团簇，则是以(SiO2)4－为基础结构，然后每增加一个单位的SiO2，得出一种新的最低能量结构，具有一定的生长规律.

图2 (SiO2)－n(n≤7)负离子团簇的最低能量结构

3.2. (SiO2)n－(n≤7)负离子团簇的相对稳定性和化学活性

为了研究团簇的相对稳定性，图3给出了(SiO2)n－(n≤7)负离子团簇的平均结合能Eb随团簇尺寸变化的规律.(SiO2)n－团簇平均结合能Eb由下式给出:

从图3可以看出，随着团簇尺寸的增加，团簇最稳定结构的平均结合能是增大的，因此团簇在生长过程中能继续释放能量.

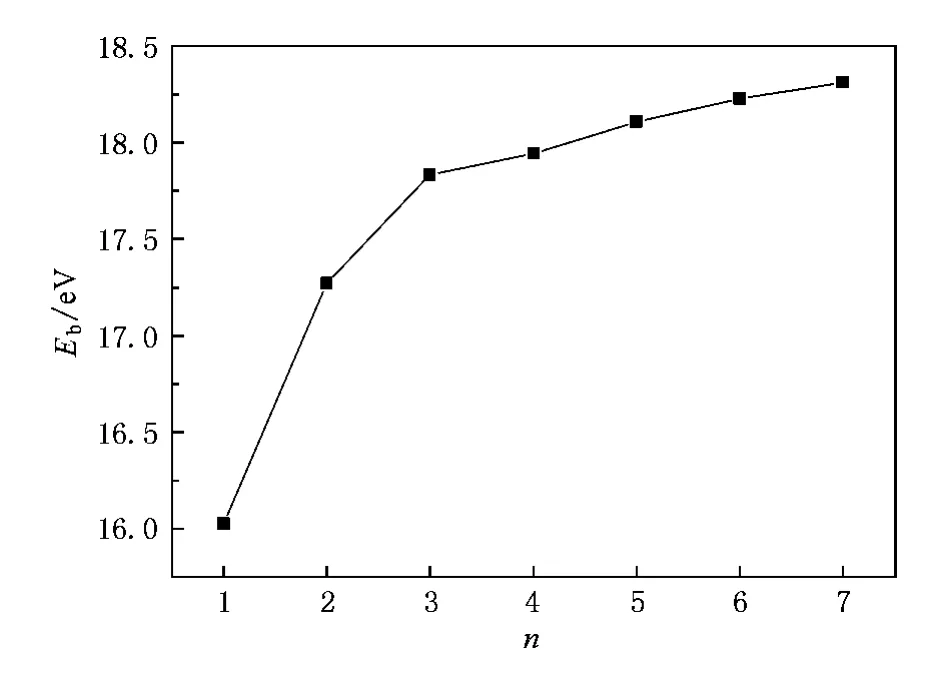
图3 (SiO2)－n(n≤7)负离子团簇最低能量结构的平均结合能

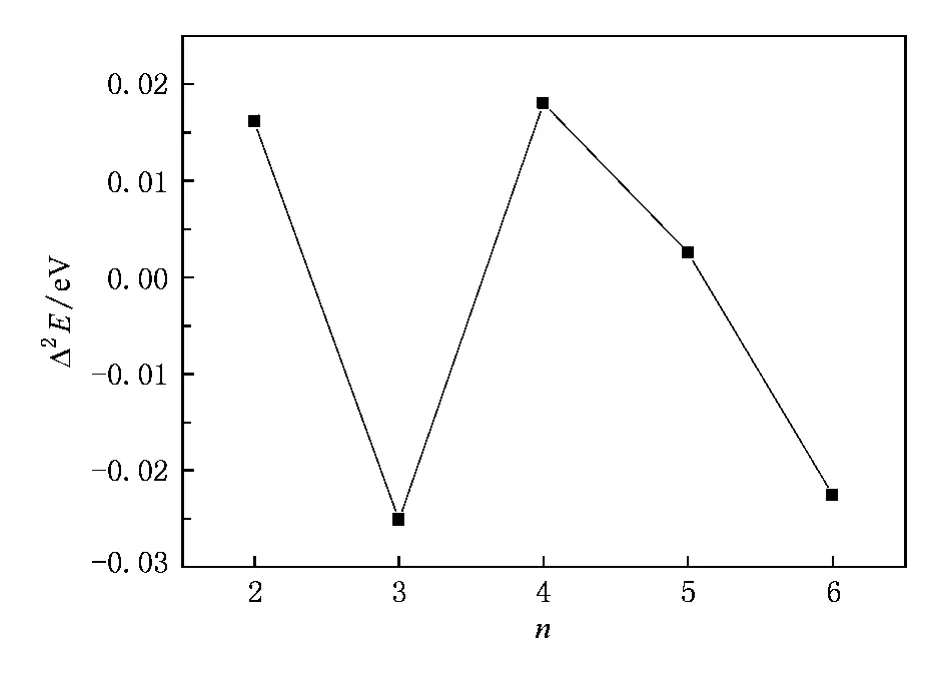
图4 (SiO2)－n(n≤7)负离子团簇能量二次差分Δ2E与分子数n的关系

能量的二阶差分Δ2E也可以用来讨论团簇的稳定性，Δ2E的表达式为

图4给出了(SiO2)n－(n≤7)负离子团簇能量二次差分随尺寸变化的关系.当n=4时，能量二次差分出现了峰值，与近邻团簇相比(SiO2)4－是比较稳定的，再结合图2中团簇结构增长趋势，表明相对于与近邻尺寸的团簇，(SiO2)4－团簇结构更加稳定.值得一提的是，徐灿等［14］用激光烧蚀法得到团簇系列［(SiO2)nO2H3］－，在其质谱中发现了n=4是团簇幻数.

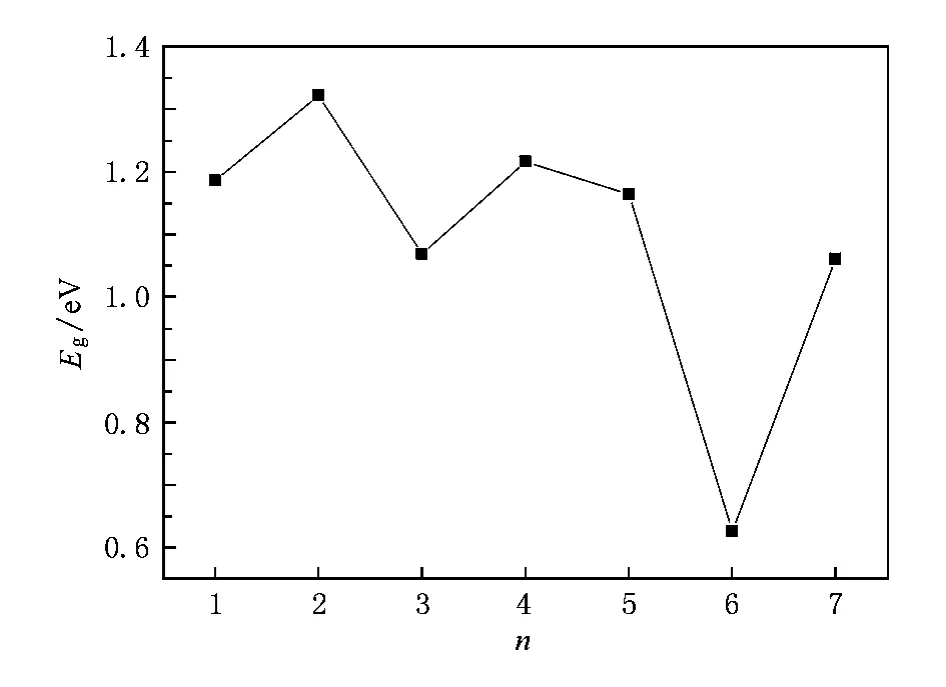
图5 (SiO2)－n(n≤7)负离子团簇最低能量结构的能隙

图5给出了团簇的最高已占据轨道与最低未占据轨道的能隙Eg随团簇尺寸的变化规律.能隙反映了电子从占据轨道向未占据轨道发生跃迁的能力，在一定的程度上代表分子参与化学反应的能力.从图5可以看出，n≤5时，曲线呈现奇-偶震荡，n=6时出现一个谷值，n=7时，曲线又有所回升.特别是n=4时，出现一个峰，与近邻尺寸的团簇相比，(SiO2)4－团簇的能隙较大，说明(SiO2)4－团簇的化学活性比较弱且比较稳定.这与前面能量二次差分的分析结果是一致的.

4. 结论

采用DFT中的GGA对(SiO2)n－(n≤7)负离子团簇的几何构型进行了优化，并对能量和频率进行了计算.结果表明，对于(SiO2)n－负离子团簇，n= 1，2时的结构是由中性(SiO2)n的结构畸变而成的，而当n≥4时，团簇的增长呈现一定的规律性.通过对结构增长、团簇能量二次差分、团簇能隙的分析，结果表明图2中的(SiO2)4－是最稳定的结构.

［1］Holmes D L 1969 Elements of Physical Geology(New York: Ronald Press)Chapt.3

［2］Jena P，Khanna S N，Rao B K 1992 Physics and Chemistry of Finite System:FromClusterstoCrystals(Boston:Kluwer Academic Pulishers)Vols.I and II

［3］Wu D L，Cheng X L，Yang X D，Xie A D，Yu X G，Deng X H 2007 Acta Phys.Sin.56 147(in Chinese)［伍冬兰、程新路、杨向东、谢安东、余晓光、邓小辉2007物理学报56 147］

［4］Li B，Yang C L，Qi K T，Zhang Y，Sheng Y 2009 Acta Phys. Sin.58 3104(in Chinese)［李兵、杨传路、齐凯天、张岩、盛勇2009物理学报58 3104］

［5］Sheng Y，Mao H P，Tu M J 2008 Acta Phys.Sin.57 4153(in Chinese)［盛勇、毛华平、涂铭旌2008物理学报57 4153］

［6］Wang H Y，Li X B，Tang Y J，Chen X H，Wang C Y，Zhu Z H 2005 Acta Phys.Sin.54 3565(in Chinese)［王红艳、李喜波、唐永建、谌晓洪、王朝阳、朱正和2005物理学报54 3565］

［7］Harkless J A W，Stillinger D K，Stillinger F H 1996 J.Phys. Chem.100 1098

［8］Nayak S K，Rao B K，Khanna S N，Jena P 1998 J.Chem. Phys.109 1245

［9］Flikkema E，Bromley S T 2003 Chem.Phys.Lett.378 622

［10］Flikkema E，Bromley S T 2004 J.Phys.Chem.B 108 9638

［11］Chu T S，Zhang R Q，Cheung H F 2001 J.Phys.Chem.B 105 1705

［12］Lu W C，Wang C Z，Nguyen V，Schmid M W，Gordon M S，Ho K M 2003 J.Phys.Chem.A 107 6936

［13］Chelikowsky J R 1998 Phys.Rev.B 57 3333

［14］Xu C，Wang W，Zhang W，Zhuang J，Liu L，Kong Q，Zhao L，Long Y，Fan K，Qian S，Li Y 2000 J.Phys.Chem.A 104 9518

［15］Nedelec J M，Hench L L 2000 J.Non-Cryst.Solids 277 106

［16］Zhang R Q，Chu T S，Cheung H F，Wang N，Lee S T 2001 Phys.Rev.B 64 113304

［17］Zhang D J，Zhang R Q 2006 J.Phys.Chem.B 110 1338

［18］Wales D J，Doye J P K 1997 J.Phys.Chem.A 101 5111

［19］Wang L S，Wu H，Desai S R，Fan J，Colson S D 1996 J.Phys. Chem.100 8697

［20］Wang L S，Desai S R，Wu H，Nicholas 1997 Z.F.Phys.D 40 36

［21］Delley B 2000 J.Chem.Phys.113 7756

［22］Perdew J P，Wang Y 1992 Phys.Rev.B 45 13244

PACC:3640，3640B，3120A

*Project supported by the National Natural Science Foundation of China(Grant No.10674114).

†E-mail:yjiazhang@foxmail.com

††Corresponding author.E-mail:shengyong69@163.com

Density functional theory study of silica clusters(SiO2)n－(n≤7)*

Zhang Yan1)†Chen Xue-Feng1)Qi Kai-Tian1)Li Bing1)Yang Chuan-Lu2)Sheng Yong1)††
1)(College of Material Science and Engineering，Sichuan University，Chengdu610065，China)
2)(College of Physics and Electronics，Ludong University，Yantai264025，China)
(Received 16 September 2009;revised manuscript received 12 October 2009)

Geometric structures of(SiO2)n－(n≤7)anion clusters are optimized by using the generalized gradient approximation density functional theory.The energy and vibrational frequency have been calculated.The lowest energy(SiO2)4－cluster is found to be more thermodynamically favored compared with other neighboring sized cluster isomers.Additionally，the lowest energy(SiO2)n－(n≥4)clusters grow up regularly based on the lowest energy(SiO2)4－cluster.

silica，anion clusters，density functional theory

book=374,ebook=374

*国家自然科学基金(批准号:10674114)资助的课题.

†E-mail:yjiazhang@foxmail.com

††通讯联系人.E-mail:shengyong69@163.com