H2+He 流体混合物在部分离解区的物态方程*

顾云军 郑君 陈志云 陈其峰蔡灵仓

(中国工程物理研究院流体物理研究所冲击波物理与爆轰波物理实验室，绵阳621900)

(2009年7月7日收到;2009年11月25日收到修改稿)

H2+He 流体混合物在部分离解区的物态方程*

顾云军 郑君 陈志云 陈其峰†蔡灵仓

(中国工程物理研究院流体物理研究所冲击波物理与爆轰波物理实验室，绵阳621900)

(2009年7月7日收到;2009年11月25日收到修改稿)

H2+He流体混合物在高温高压下由于氢的离解化学反应形成由H2，H，He三种粒子构成的混合体系，此时粒子间的相互作用较为复杂，离解能也会由于粒子间的这种复杂相互作用而降低.本文利用自洽流体变分理论来研究部分离解区H2+He流体混合物的高温高压物态方程，模型考虑了各种粒子间的相互作用及由温致和压致效应引起的离解能降低的自洽变分修正，并通过自洽流体变分过程对非理想的离解平衡方程求解得到粒子数密度分布，进而对自由能求导获得体系的热力学状态参量.计算结果与已有的冲击波实验数据、蒙特卡罗模拟及其他理论计算进行了比较.

H2+He流体混合物，物态方程，部分离解，自洽流体变分理论

PACC:0570C，6400

1. 引言

氢、氦是宇宙中丰度最高的两种元素，也是某些星体如土星、木星等内部的主要物质组成.尽管其电子结构较为简单，但是其高压下的行为却十分复杂，对其混合物尤其如此.近代自然科学的许多领域如天体演化、激光聚变等均要涉及氢、氦及其流体混合物在高温高压下的状态特性及过程.因此，对高温高密度流体氢、氦及其混合物物态方程的研究将有助于对某些天体物理问题的理解［1—4］，对新的能源工程如惯性约束核聚变(ICF)也具有重要意义.高压实验技术的不断发展，使得人们在单质液态氢、氘、氦高温高压物态方程研究方面已经取得了巨大进展［5—10］，但是关于其混合物的理论和实验研究工作比较有限［11—15］.为了描述混合分子流体，Ree［13］引入了范德瓦耳斯等效单组分流体模型(vdw1f)，该模型将多组分粒子体系间的相互作用等效为单组分粒子间的相互作用处理，从而大大简化了对混合体系统计热力学的计算.陈其峰等［12］利用该模型加量子力学一级修正研究了0—60 GPa压力和50—7000K温度范围内不同摩尔比H2+He流体混合物的高压物态方程，理论计算结果与蒙特卡罗(MC)模拟基本一致.但vdw1f模型没有考虑高压下氢分子的离解及其对混合物体系状态方程的贡献.Saumon和Chabrier等［4］提出了基于纯氢和纯氦物态方程的组分平均模型，尽管该模型引入了氢的离解，但却不能考虑混合物中异组粒子如H2-He和H-He间的相互作用对混合体系的影响.为了解决高密度下分子原子流体的离解和电离，陈其峰等［16—20］建立了自洽流体变分理论模型(SFVT)，并应用到对高密度流体氮、氧、氦、氙等物态方程的计算，得到了与冲击波实验和其他理论方法相一致的结果.本文将SFVT模型推广应用到对H2+He流体混合物部分离解区物态方程的计算，预测了较宽密度(0.1—2.0 g/cm3)和温度(1000—7000K)范围内的物态方程，模型计算结果与已有的实验和其他理论结果进行了比较.

2. 理论计算方法

由于氢分子的离解能(4.478 eV)较氢原子的电离能(13.6 eV)以及氦原子的一次、二次电离能(24.6 eV，54.4 eV)都要低得多，因此在研究H2+ He流体混合物的高温高压物态方程时，首先需要考虑氢分子的离解化学反应对混合体系热力学性质的影响.当氢分子发生离解化学反应时，原来的二元流体混合物(H2和He组成)将形成

由氢分子(H2)、氢原子(H)和氦原子(He)构成的三元混合体系，粒子间相互作用也由原来的三种(He-He，H2-H2和H2-He)增加到7种(He-He，H2-H2，H2-He，H-H，H-He，H-H2和H2-H-He)，粒子间的相互作用更加复杂.在这些相互作用中，两体相互作用占主导，而H2-H-He之间的三体相互作用对整个系统而言贡献不大.因此为了简化计算，在这里暂时忽略三体效应.

设在某一温度T和体积V时，H2+He流体混合物经历分子离解，流体混合物由H2，H和He组成，其粒子数分别记为N0，N1和N2，未离解前H2总数记为N00，He的初始摩尔分数为xHe=N2/(N00+ N2)，体系的亥姆霍兹(Helmholtz)自由能为

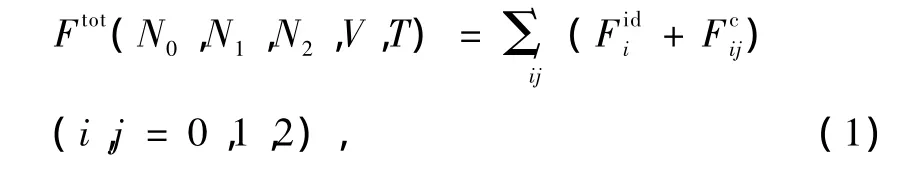
这里，i，j=0，1，2(0=H2，1=H，2=He);Fid和Fc分别为粒子的理想自由能和位形作用自由能.

理想自由能可写为

其中，D=4.478 eV是氢分子的离解能［21］，上标tr，r，v，el分别代表平动、转动、振动、内部电子运动对理想自由能的贡献.

位形作用自由能可以表示为［16］

其中，Fhs和Fpert分别表示硬球混合超额自由能［22］和微扰自由能［16］.

式中，

这里，di是粒子的硬球直径，在这里作为变分参数，通过(5)式对自由能求极小值得到;gHS(r，η)为硬球径向分布函数，Φ(r)为粒子间的相互作用势，选用exp-6形式.H2-H，H-H，H2-H，H2-He，He-He势参数分别取自文献［21］和［11］，He-H势参数采用Lorentz-Berthelot混合法则得到［23］.

式中，

这里，K是离解平衡常数，ΔD是粒子间相互作用对离解能的修正，Tv=6338.2 K和Tr=87.58 K分别是H2的振动和转动特征温度［21］.在给定温度T和体积V下，方程(10)含有两个未知数，对其求解还需要加上氢的粒子数守恒关系

这样，粒子数N0和N1可以根据方程(5)，(10)和(11)通过自洽迭代求解得到.计算出粒子数分布后，根据方程(1)可以求出自由能，进而运用热力学公式得到混合物体系的压强P和内能E

雨贡纽曲线(Hugoniot)还必须满足兰金-雨贡纽(Rankine-Hugoniot)关系

这里，E0，P0，V0分别为初始比内能、压强和比容，EH，PH，VH分别为冲击压缩后对应的状态参数.

3. 计算结果与讨论

利用上述方法，计算了温度1000—7000K不同组分摩尔比(［H2］∶［He］=3∶1，1∶1，1∶3，对应xHe=0.25，0.5，0.75)H2+He流体混合物的等温状态方程，计算结果见表1及图1所示.作为比较，表1还给出了MC模拟［13］和其他模型计算结果［11，12］.在这些计算中均没有考虑H2的离解效应，可以看出本文计算结果在温度为1000和4000K时与MC模拟和其他模型计算结果基本一致，在温度为7000K时本文计算的压力值稍偏低.在温度较低时(1000和4000K)，H2离解份额较少，因此几种计算结果基本趋于一致;随着温度升高到7000K，H2的离解份额逐渐增加，分子离解使系统能量降低，同时增加了粒子数密度，系统能量降低使系统压力降低，但粒子数密度增加却使压力增加，这两个相反的过程有一部分抵消.因此本文计算压力值只是稍偏低，只有当前一个过程占主导地位时才会出现明显的压力变化.为了进一步分析分子离解对混合物体系热力学性质的影响，图1还给出了没有考虑H2离解时双组分流体变分理论FVT计算结果(图中用短划线表示).可以发现，在一定的压力密度范围离解模型SFVT和非离解模型FVT计算结果基本一致，在此区间分子离解对体系等温压缩线的影响可以忽略;随着压力和密度的增加，两种计算结果逐渐偏离，分子离解对体系热力学性质的影响开始逐渐显现出来，导致等温压缩线出现明显的软化(即同样的压力下，SFVT模型计算结果具有更大的压缩度).此外还可以看出，随着温度升高分子离解对体系热力学性质的影响逐渐向低密度区域扩展，表明温致离解效应在低密度情况下较为显著，而压致离解主要出现在较高压力密度条件下.此外，从图1还可以发现，H2离解对体系热力学性质的影响是渐进的，没有出现跃变，表明氢的离解是一个连续的过程.

表1 本文计算的不同组分H2+He流体混合物压力与MC及其他计算结果的比较

图1 不同组分H2+He流体混合物等温压缩线(a)T=1000K，(b)T=4000K，(c)T=7000K

冲击压缩尤其是冲击温度测量实验为各种理论模型的检验提供了良好的机遇，强冲击波作用下分子离解所导致的“冲击致冷现象”可以为分子离解提供直接的证据［10，14，24］，因为分子离解将会吸收能量从而降低温度.与前面所说对压力的影响不一样，分子离解对冲击温度的影响是单方面的，只能是降低的，与压力相比冲击温度对分子离解更加敏感，因此对冲击温度的预测精度直接关系到理论模型的合理与否与适用范围.为了同已有的实验数据进行比较分析，计算了混合摩尔比［H2］∶［He］=1∶1.21，6.21∶1两种不同初始条件下H2+He流体混合物的Hugoniot曲线和冲击温度(初始条件分别对应于文献［14］和［15］)，结果如图2和图3所示，可以看出本文计算结果在P-V和T-V平面上均能够较好地再现文献［14］和［15］报道的实验数据.图3还给出了没有考虑H2离解时双组分流体变分理论FVT计算结果.可以看出，两种计算(SFVT和FVT)对于文献［14］和［15］的一次冲击温度均能够给予合理解释，此时氢的离解度小于5%，体系仍然是主要由H2和He组成的二元混合物，只有少量的H存在，因此分子离解对冲击温度影响不大.随着冲击温度的进一步升高，分子离解份额逐步增加，表现为H2+He流体混合物具有更大的压缩性;对于文献［14］的二次冲击过程，氢的离解度上升到～30%，此时SFVT模型预测的二次冲击温度与实验值基本一致，而FVT给出的冲击温度明显偏高(比实验值高约40%)，很明显，这是因为分子离解吸收了大量冲击能量所致.另外，在图3中还给出了用同样的SFVT和FVT模型计算的液体H2的冲击温度和实验数据的比较，可以看出SFVT对单组分H2的描述也是成功的.

图2 不同组分H2+He流体混合物计算Hugoniot曲线与实验数据的比较

图3 不同组分H2+He流体混合物及液体H2计算冲击温度与实验数据的比较

4. 结论

本文利用自洽流体变分理论(SFVT)研究了具有范德瓦耳斯粒子间相互作用和分子离解化学反应的H2+He流体混合物的高压状态方程，研究了温致和压致离解现象对流体混合物热力学性质的影响，并从等温线和冲击Hugoniot线两个方面考核了SFVT模型的适用性，研究表明H2的离解是一个连续的过程，SFVT模型对于构建H2+He流体混合物在部分离解区的高温高压状态方程是可行的.

［1］Kowalski P M，Mazevet S，Saumon D，Challacombe M 2007 Phys.Rev.B 76 075112

［2］Redmer R，Holst B，Juranek H，Nettelmann N，Schwarz V 2006 J.Phys.A 39 4479

［3］Chabrier G，Saumon D，Potekhin A Y 2006 J.Phys.A 39 4411

［4］Saumon D，Chabrier G，van Horn H M 1995 Astrophys.J. Suppl.Ser.99 713

［5］Eggert J，Brygoo S，Loubeyre P，McWilliams R S，Celliers P M，Hicks D G，Boehly T R，Jeanloz R，Collins G W 2008 Phys.Rev.Lett.100 124503

［6］Boriskov G V，Bykov A I，II′kaev R I，Selemir V D，Simakov G V，Trunin R F，Urlin V D，Shuikin A N 2005 Phys.Rev.B 71 092104

［7］Boehly T R，Hicks D G，Celliers P M，Collins T J B，Earley R，Eggert JH，Jacobs-PerkinsD，MoonSJ，VianelloE，Meyerhofer D D，Collins G W 2004 Phys.Plasmas 11 L49

［8］Knudson M D，Hanson D L，Bailey J E，Hall C A，Asay J R，Deeney C 2004 Phys.Rev.B 69 144209

［9］Nellis W J，Weir S T，Mitchell A C 1999 Phys.Rev.B 59 3434

［10］Holmes N C，Ross M，Nellis W J 1995 Phys.Rev.B 52 15835

［11］Xue X Y，Sun J X 2007 Chem.Phys.337 39

［12］Chen Q F，Cai L C，Chen D Q，Jing F Q，Zhao X G 2003 Chin. J.High Pressure Phys.17 173(in Chinese)［陈其峰、蔡灵仓、陈栋泉、经福谦、赵宪庚2003高压物理学报17 173］

［13］Ree F H 1983 J.Chem.Phys.78 409

［14］Gu Y J，Chen Q F，Cai L C，Chen Z Y，Zheng J，Jing F Q 2009 J.Chem.Phys.130 184506

［15］Ternovoi V Y，Kvitov S V，Pyalling A A，Filimonov A S，Fortov V E 2004 JETP Lett.79 6

［16］Chen Q F，Cai L C，Zhang Y，Gu Y J，Jing F Q 2006 J. Chem.Phys.124 074510

［17］Chen Q F，Cai L C，Zhang Y，Gu Y J 2008 J.Chem.Phys. 128 104512

［18］Chen Q F，Zhang Y，Cai L C，Gu Y J，Jing F Q 2007 Phys. Plasmas 14 012703

［19］Zhang Y，Chen Q F，Gu Y J，Cai L C，Lu T C 2007 Acta Phys. Sin.56 1318(in Chinese)［张颖、陈其峰、顾云军、蔡灵仓、卢铁城2007物理学报56 1318］

［20］Chen Q F，Cai L C，Gu Y J，Gu Y 2009 Phys.Rev.E 79 016409

［21］Juranek H，Redmer R 2000 J.Chem.Phys.112 3780

［23］van Thiel M，Ree F H 1996 J.Chem.Phys.104 5019

［24］Ross M 1987 J.Chem.Phys.86 7110

PACC:0570C，6400

*Project supported by the National Natural Science Foundation of China(Grant No.10674120)and the Science and Technology Development Foundation of China Academy of Engineering Physics(Grant Nos.2007A01002，2009B01006).

†Corresponding author.E-mail:chen_qifeng@iapcm.ac.cn

The equation of state of H2+He fluid mixture in the region of partial dissociation*

Gu Yun-Jun Zheng Jun Chen Zhi-Yun Chen Qi-Feng†Cai Ling-Cang
(National Key Laboratory of Shock Wave and Detonation Physics Research，Institute of Fluid Physics，China Academy of Engineering Physics，Mianyang621900，China)
(Received 7 July 2009;revised manuscript received 25 November 2009)

The H2+He fluid mixture will be dissociated into a three-component mixture composed of H2molecules，H and He atoms at high temperatures and high pressures.The dissociation energy of H2molecule will be lowered due to the interactions between all these particles.In this paper，the self-consistent fluid variational theory is used to calculate the equation of state of H2+He fluid mixture in the region of partial dissociation，in which the various interactions between particles and the correlation contributions to the dissociation energy caused by both the temperature and pressure effects are taken into account.The dissociation degree and thermodynamic parameters are obtained from nonideal dissociation equilibrium，which is determined self-consistently by the free energy function.Comparison was made with the available shock-wave experiments，other theoretical calculations and Monte Carlo simulations.

H2+He fluid mixture，equation of state，partial dissociation，self-consistent fluid variational theory

book=360,ebook=360

*国家自然科学基金(批准号:10674120)和中国工程物理研究院科学技术发展基金(批准号:2007A01002，2009B01006)资助的课题.

†通讯联系人.E-mail:chen_qifeng@iapcm.ac.cn