包含伺服约束非完整系统的Noether-Mei对称性

王小明,李元成,张佩玲,荆宏星

(1.中国石油大学物理科学与技术学院,山东东营 257061;2.北京国电清新环保技术股份有限公司,北京 100036)

包含伺服约束非完整系统的Noether-Mei对称性

王小明1,李元成1,张佩玲2,荆宏星1

(1.中国石油大学物理科学与技术学院,山东东营 257061;2.北京国电清新环保技术股份有限公司,北京 100036)

根据系统的运动微分方程,给出伺服约束非完整系统的新对称性的定义和判据,得到了系统的 Noether-Mei对称性导出的Noether守恒量和Mei守恒量。举例说明结果的应用。

伺服约束;非完整系统;Noether-Mei对称性;守恒量

力学系统的对称性与守恒量的研究在数学、力学和物理学上都具有重要的意义。近代寻求守恒量的对称性方法主要有 Noether对称性[1-3],Lie对称性[2-4]和Mei对称性[5-10]。相应的守恒量有 Noether守恒量[1-3],Hojman守恒量[11,12]和Mei守恒量[13]。近几年对力学系统对称性与守恒量的研究取得了很大进展。Mei研究了包含伺服约束非完整系统的Lie对称性与守恒量[14,21]以及 Lagrange系统的统一对称性[15],最近,梅凤翔、吴惠彬等研究了各种力学系统的联合对称性和统一对称性[16-20]。笔者研究包含伺服约束非完整系统的Noether-Mei对称性,给出系统的Noether-Mei对称性的定义和判据,并由此找到系统的Noether守恒量和Mei守恒量。

1 系统的运动微分方程

设力学系统的位形由 n个广义坐标 qs(s=1,…,n)确定,并受到通常的理想双面 Chetaev型非完整约束

以及 r个伺服约束:n1个完整约束及 n2(n2=r-n1)个非完整约束

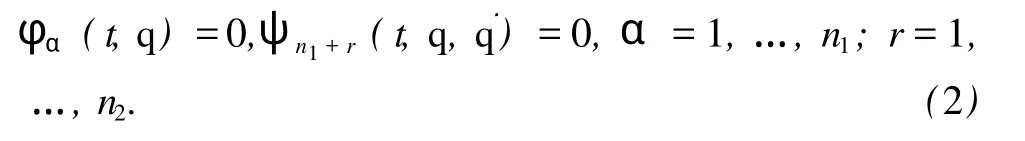
称方程(1)为第一类约束,方程 (2)为第二类约束。对第一类约束,由Appell-Chetaev定义,有

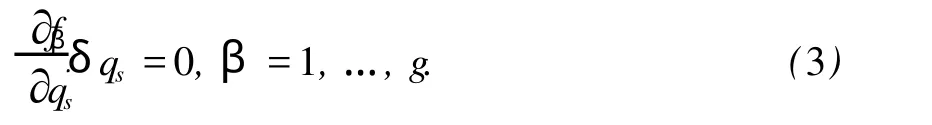
第一类约束反力的虚功之和为零,但第二类约束反力的虚功一般异于零。在为第一类约束所允许的虚位移中间,存在一些使第二类约束反力在其上作功为零的虚位移,设这些虚位移满足 j个关系

系统的运动微分方程为

其中

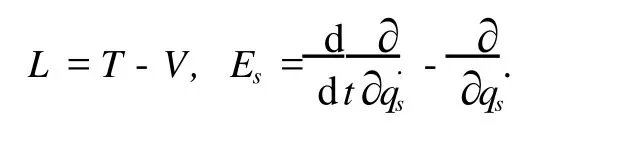
式中,L为 Lagrange函数;Qs为非势广义力;λβ,uk为不定乘子;Es为 Euler算子。

当 r=j时,方程 (5)联同方程 (1),(2)组成为确定 n+g+r个变量 q1,…,qn,λ1,…,λg,u1,…,ur的 n+g+r个方程。在非奇异的假设下,展开方程(5),可求得所有广义加速度,记作

将方程(1)和方程(2)中的第二式对 t求一阶导数,并将方程(2)中的第一式对 t求二阶导数,可得到包含对为线性的 g+r个方程,再将式 (6)代入这 g +r个方程,并消去 ¨qs,可得 g+r个乘子λβ和 uk的一组代数方程,解此代数方程,可得

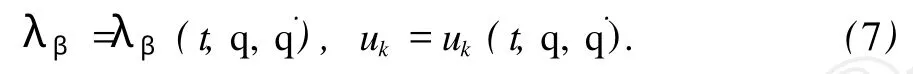
将式(7)代入方程 (6),可求得所有广义加速度,记作

方程 (7)为非完整系统 (1),(2),(5)相应的完整系统的运动方程。

2 系统的 Noether-M ei对称性的定义和判据

定义 如果包含伺服约束的非完整系统的对称性既是Noether对称性又是Mei对称性,则称该对称性为系统的Noether-Mei对称性。

引入时间和广义坐标的无限小变换

式中,ε为无限小参数;ξ0和ξs均为无限小生成元。

约束方程(1),(2)在无限小变换下的不变性为

对包含伺服约束的非完整系统,Noether等式为

其中

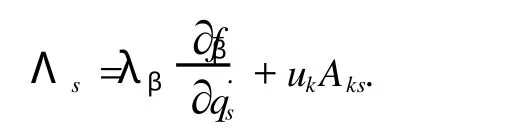
Mei对称性的判据方程为

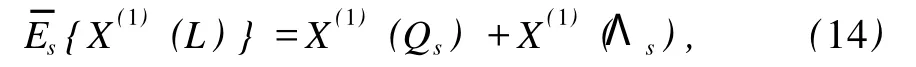
其中

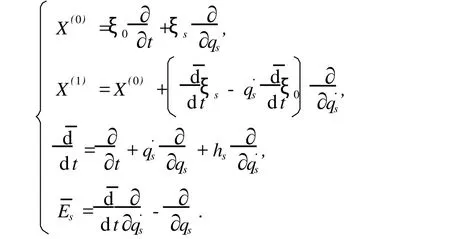
判据 对于伺服约束非完整系统,如果存在规范函数 GN=GN(t,q,˙q),无限小生成元ξ0,ξs满足等式 (10)～(12)和

则相应对称性为伺服约束非完整系统的 Noether-Mei对称性。

3 系统的 Noether-M ei对称性导致的守恒量

伺服约束非完整系统的Noether-Mei对称性在一定条件下可导出Noether守恒量和Mei守恒量。

命题 1 对于伺服约束非完整系统,Noether-Mei对称性可导致Noether守恒量

证明 因为伺服约束非完整系统的 Noether-Mei对称性一定是Noether对称性,则存在一个规范函数 GN=GN(t,q,˙q)满足 Noether等式 (13),根据判据系统存在守恒量(16)。

命题 2 对于伺服约束非完整系统,如果存在规范函数 GM=GM(t,q,˙q),满足方程

则系统Noether-Mei对称性可导致Mei守恒量

证明 因为伺服约束非完整系统的 Noether-Mei对称性一定是Mei对称性,则系统的Mei对称性判据方程(14)成立,利用式 (14),(17)能够证明系统存在Mei守恒量(18)。

4 说明性例子

一质量平面 P可在一水平固定面 oxy上平动地滑动。在平面 P上有一半径为 R,质量为M的均质圆球可无滑动地滚动。平面 P的运动用伺服装置自动地调节,以使球心以角速度ω相对固定轴 oz匀速转动,研究此伺服约束系统的 Noether-Mei对称性与守恒量。

首先写出系统的运动微分方程。设 u,v为平面P上的一点A相对轴 ox,oy的坐标。平面的位置由这两个参数确定。设ξ,η为球心 G的前两个坐标, p,q,r为球的瞬时角速度在轴 ox,oy,oz上的投影, ψ,θ,φ为 Euler角,有

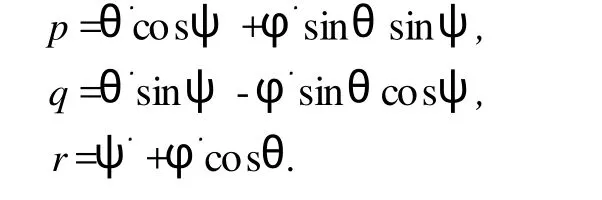
球沿平面 P无滑动地滚动的非完整约束条件为

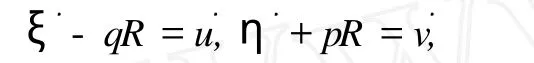
伺服约束为

使第二类约束反力所做的功为零的虚位移为

进而有

球的动能表示为

令 q1=ξ,q2=η,q3=ψ,q4=θ,q5=φ,取无限小生成元:

生成元(19)满足式(15),可知生成元(19)是包含伺服约束非完整系统的Noether-Mei对称性。将式 (19)代入式(13)有规范函数

由命题 1得由系统 Noether-Mei对称性导致的Noether守恒量为

将式 (19)代入式(17),有

由命题2得

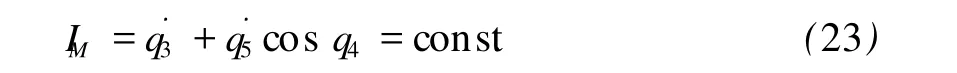
IM即为由系统的 Noether-Mei对称性得到的Mei守恒量。

[1] 李子平.经典和量子约束系统及其对称性质 [M].北京:北京工业大学出版社,1993.

[2] 赵跃宇,梅凤翔.力学系统的对称性与不变量[M].北京:科学出版社,1999.

[3] 梅凤翔.李群和李代数对约束力学系统的应用 [M].北京:科学出版社,1999.

[4] 梅凤翔.具有可积微分约束的力学系统的 Lie对称性[J].力学学报,2000,32(4):466-472.

MEI Feng-xiang.Lie symmetries of mechanical system with integral differential constraints[J].Acta Mechanica Sinica,2000,32(4):466-472.

[5] MEI F X,ZHU H P.Lie symmetries and conserved quantities for the singular Lagrange system[J].Journal

ofBeijing Institute of Technology,2000,9(1):11-14.

[6] 梅凤翔.关于 Noether对称性、Lie对称性和形式不变性[J].北京理工大学学报,2001,21(4):535-536.

MEI Feng-xiang.On Noether symmetry.Lie symmetry and form invariance[J].Journal of Beijing Institute of Technology,2001,21(4):535-536.

[7] MEI F X.Form invarlance ofAppell equations[J].Chinese Physics,2001,10(3):177-180.

[8] WANG S Y,MEI F X.On the form invariance ofNielsen equations[J].Chinese Physics,2001,10(5):373-375.

[9] WANG S Y,MEI F X.Form invariance and Lie symmetry of equations of non-holonomic systems[J].Chinese Physics,2002,11(1):5-8.

[10] ZHANG Y,MEI F X.For m invariance for systemsof generalized classicalmechanics[J].Chinese Physics,2003,12 (10):1058-1061.

[11] HOJMAN SA.A new conservation law constructed without using either Lagrangians or Hamiltonians[J].J Phys A:Math Gen,1992,25:L291-L295.

[12] 张宏彬,陈立群,刘荣万,等.广义 Hojman定理[J].物理学报,2005,54(6):2489-2493.

ZHANG Hong-bin,CHEN Li-qun,L I U Rong-wan, et al. The generalized Hojman´s theorem[J].Acta Physica Sinica,2005,54(6):2489-2493.

[13] 王树勇,尚玫,梅凤翔.完整力学系统的形式不变性与非 Noether守恒量 [J].北京理工大学学报,2003, 23(3):271-273.

WANG Shu-yong,SHANG Mei,MEI Feng-xiang. Form invariance and non-Noether conserved quantity of holonomic mechanical system[J].Journal ofBeijing Institute of Technology,2003,23(3):271-273.

[14] 梅凤翔.包含伺服约束的非完整系统的 Lie对称性与守恒量[J].物理学报,2000,49(7):1207-1210.

MEI Feng-xiang.Lie symmetries and conserved quantities of Nonholonomic systems with Servoconstr Aints [J].Acta Physica Sinica,2000,49(7):1207-1210.

[15] MEI F X,XU X J,ZHANG Y F.A unified symmetryof Lagrangian systems[J].Acta Mechanica Sinica,2004, 20(6):668-671.

[16] WU H B.Lie-form invariance of the Lagrange system [J].Chinese Physics,2005,14(3):452-454.

[17] XU X J,Q I N M C,MEI F X.Unified symmetry of holonomic mechanical systems[J]. Chinese Physics, 2005,14(7):1287-1289.

[18] 梅凤翔.Lagrange系统的 Noether-Lie对称性[J].北京理工大学学报,2005,25(4):283-285.

MEI Feng-xiang.Noether-Lei symmetry of Lagrange system[J].Journal of Beijing Institute of Technology, 2005,25(4):283-285.

[19] 李元成,夏丽莉,赵伟,等.机电系统的统一对称性[J].物理学报,2007,56(9):5037-5040.

L I Yuan-cheng,XI A Li-li,ZHAO Wei,et al.Unified symmetry of mechanico-electrical systems[J]. Acta Physica Sinica,2007,56(9):5037-5040.

[20] XI A L L,L I Y C,HOU Q B,et al.Unified symmetry of nonholonomic mechanical systemswith variable mass [J].Chinese Physics,2006,15(5):903-906.

[21] 董文山.非完整力学系统的高阶 Routh方程及其正则形式[J].中国石油大学学报:自然科学版,2008, 32(3):165-168.

DONGWen-shan.Higher order Routh equations of a non-holonomic mechanical system and its canonical for m[J].Journal of China University of Petroleum(Edition ofNatural Science),2008,32(3):165-168.

(编辑 修荣荣)

Noether-M ei symmetry of nonholonom ic system s with servoconstra ints

WANG Xiao-ming1,L I Yuan-cheng1,ZHANG Pei-ling2,J ING Hong-xing1
(1.Collage of Physics Science and Technology in China University of Petroleum,Dongying257061,China; 2.Beijing SPC Enviroment Protection Tech Co.,LTD,Beijing100036,China)

The definition and the criterion of a Noether-Mei symmetry for the nonholonomic systems with servoconstraints, aswell as the Noether conserved quantity and theMei conserved quantity deduced from the Noether-Mei symmetry for the system were given.An example was given to illustrate the application of the results.

servoconstraints;nonholonomic systems;Noether-Mei symmetry;conserved quantity

O 313

A

10.3969/j.issn.1673-5005.2010.02.033

1673-5005(2010)02-0163-03

2009-05-13

王小明(1979-),女(蒙古族),内蒙古人,讲师,硕士,主要从事理论力学方面的研究。