基于疲劳可靠性优化设计的深水导管架平台多级模糊选型

杨秀娟,修宗祥,闫相祯,冯永训

(1.中国石油大学储运与建筑工程学院山东东营 257061;2.胜利工程设计咨询公司山东东营 257026)

基于疲劳可靠性优化设计的深水导管架平台多级模糊选型

杨秀娟1,修宗祥1,闫相祯1,冯永训2

(1.中国石油大学储运与建筑工程学院山东东营 257061;2.胜利工程设计咨询公司山东东营 257026)

分析深水导管架平台方案优选的系统决策问题,给出四种初始设计方案,将基于谱分析方法求得平台的系统名义疲劳可靠性指标作为一项关键约束对平台方案进行优化。根据优化后各方案的最优结构性能参数,综合考虑影响深水导管架平台选型的各种因素,由二元对比方法确定影响因素的权重以及相对隶属度,最终采用三级模糊优选方法对优化后的方案进行模糊优选,并以 200 m水深导管架海洋平台作为实例进行分析。结果表明,与传统分析方法相比,先由优化分析得到各初始方案的最优结构性能参数,可以为模糊选型提供准确的定量化指标,减少了模糊因素,更有利于对深水导管架平台设计方案做出合理的评价。

深水导管架平台;优化设计;谱分析;三级模糊优选;疲劳可靠性指标

深水导管架平台由于工作水深较大,施工方便等优点,很快得到推广和发展。通常深水导管架平台结构非常复杂,体积庞大,造价昂贵,其所处海洋环境极其复杂和恶劣,因此如何选择合理的结构型式方案及设计参数,是深水导管架平台设计的首要问题。随着水深的增加,随机波浪引起的平台动力响应更加明显,疲劳可靠性也成为影响深水导管架平台设计与选型的一项重要因素。传统的设计方法首先是结构型式方案的优选,然后才是特定型式下设计参数的优化[1-2]。由于初始方案并非一定是该平台型式下的最优方案,因此基于初始方案技术指标的平台模糊选型容易造成误判。针对此问题,笔者以 200 m水深导管架为例,由工程实际给出几种初始方案,根据结构优化设计理论,将由基于谱分析法求得的平台结构系统名义疲劳可靠性指标作为一项重要约束条件进行优化,得到各方案的最优设计参数,再采用三级模糊决策理论进行模糊优选,得到最佳方案。

1 深水导管架海洋平台的优化

将平台的优化分为静力性能优化和动力性能优化两部分。首先进行极限静力载荷工况下的导管架海洋平台静力优化设计,将导管架平台质量作为优化的目标函数,平台构件强度、稳定性、结构变形等作为约束条件,得到一组初步的优化结果序列。然后在静力优化设计结果的基础上,考虑随机波浪载荷下平台的动力响应特性,将平台固有频率和安全疲劳可靠性指标作为约束条件进行动力优化设计,最终得到最优的结果序列。

导管架海洋平台结构动力优化设计的数学模型为[3]

式中,X为设计变量的向量,包括构件的直径和壁厚;W(D,t)为导管架平台质量;fi为平台的固有频率和分别为固有频率的上、下界;βs为平台系统疲劳安全名义可靠性指标为 βs的下限值;与为设计变量 x的上、下限。

2 随机疲劳寿命可靠性分析

2.1 谱分析

谱分析方法将平台结构的疲劳环境作为随机过程来处理,能较准确地描述海洋波浪的能量沿整个频率范围的分布,具有较高的计算精度。设 Sηη(ω)和 Sσσ(ω)分别为平稳正态随机波浪过程η(t)与平稳正态随机交变应力过程σ(t)的功率谱密度函数,则有

式中,H(ω)为传递函数。

选定波浪谱后,采用时间域作用规则波法来确定传递函数。令平台受给定波幅和圆频率的规则波作用,采用有限元法对导管架平台结构进行动力响应分析。将所得到的关键部位的响应幅值与波幅相比可得到该圆频率下传递函数的值。取一系列不同的圆频率按上述方法计算,就可得到传递函数 H (ω)关于ω的分布规律。

2.2 疲劳寿命

当应力范围的短期分布为 Rayleigh分布时,考虑雨流修正[4],由 n个短期海况组成的长期应力参数Ω为

式中,λi为第 i海况的雨流修正系数;σsi和 f0i分别为第 i海况的均方根应力与跨零率。

σsi和 f0i可通过功率谱密度函数的矩求得,λi计算式为

其中

式中,εi为带宽系数。

根据W irsching模型[5],结构疲劳寿命为

式中,A,B和Δ均为随机变量,且认为服从对数正态分布。

疲劳寿命 Tf也是一个对数正态分布的随机变量,失效概率为

式中,Φ为标准正态函数;TD为设计寿命;β为可靠性指标。

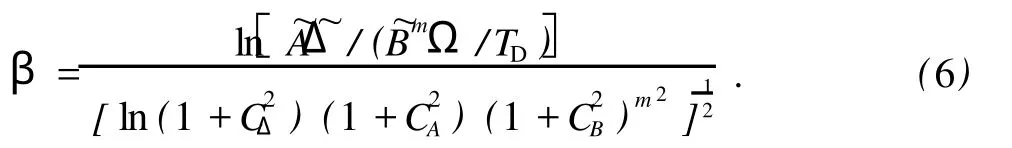
式中,~Δ,~A,~B分别为Δ,A,B的中值;CΔ,CA,CB为对应的变异系数。

2.3 导管架系统疲劳可靠性

由 n个失效单元组成的并联系统中,失效单元E1,E2,…,En依次发生疲劳破坏形成一个失效途径,该失效途径的失效概率可定义为[6]

式中,Ti为第 i个失效单元在其之前无其他单元破坏情况下的疲劳寿命;Ti/1,2,…,j为在第 1,2,…,j单元依次破坏情况下第 i个失效单元的疲劳寿命。

考虑每个单元破坏后会导致平台剩余构件的应力再重新分配,根据Miner线性累积损伤理论,可得

式中,Ωi为第 i个失效单元在其他单元未破坏情况下的应力参数;Ωi/1,2,…,j为单元 E1,E2,…,Ej依次破坏后引起结构内载荷重新分配后失效单元 Ei的应力参数。

对并联系统中所有失效单元列出式 (8)后,根据式(7)可得该失效途径的疲劳失效概率为

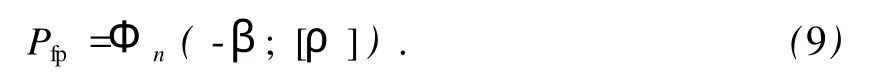
式中,Φn为 n维标准正态分布函数;[ρ]为相关系数矩阵;β为各失效单元的可靠性指标组成的矢量。

当平台系统包含 k个关键失效途径时,k个失效途径串联的疲劳失效概率为

其中

式中,Φk为 k维标准正态分布函数;βe为由等效可靠性指标组成的矢量;[ρe]为相关系数矩阵;为等效敏感性系数矢量。

3 深水导管架平台方案模糊优选模型

3.1 三级模糊优选模型

海洋平台结构型式的优选受到大量确定性及模糊性因素的影响,而且这些影响因素具有不同的层次和类别,同时各影响因素之间也具有很强的相关性,为了防止出现大量“泯没”影响因素的情况,采用三级模糊优选决策理论[7],对平台型式进行优选。

结合深水导管架平台实际工程情况,建立如下因素集:u1为平台结构变形适应情况,u2为平台冲击荷载承受能力,u3为平台对环境影响程度,u4为平台可重复利用性,这 4个因素属于平台的普通性能指标,作为第一层,进行一级模糊优选;u5为平台施工时间,u6为平台建造与安装难度,u7为材料及设备供用,这 3个因素是平台的设计施工指标,为次重要因素,作为第二层,进行二级模糊优选;u8为平台连续生产情况,u9为平台服役期维护费用情况, u10为平台疲劳安全性能,u11为平台制造成本,u12为动力可靠性,u13为结构稳定性,这些是对深水平台选型影响最大的服役指标,作为第三层,进行三级模糊优选。根据以上 11个因素的类型、层次进行如下划分:

设第 i层的因素集 U={u1,u2,…,un},决策集 V= {v1,v2,…,vm},相对隶属度矩阵为

i级因素集 ui中各因素的权重 Wi=(ω1,ω2,…, ωn),则对第 i层因素优选矩阵 Ri和权重集Wi进行模糊运算,可以得到第 i级模糊优选结果Bi,

其中,“·”为模糊算子。采用加权平均法得到 Bi以后,即可带入下一级模糊优选矩阵 Ri+1中继续进行分析,以此类推,最终可以得到第三级模糊优选结果。

3.2 相对隶属度的计算

定量指标的相对隶属度公式采用越大越优型与越小越优型两类[8]。定性指标的相对隶属度,采用二元对比方法,将海洋平台设计选型的模糊影响因素量化,从而得到各因素的相对隶属度。对于因素集中第 i个因素 ui,各方案进行优越性的二元对比,设 vk与 vl为决策集两种方案,eikl表示优越性的定性排序标度,

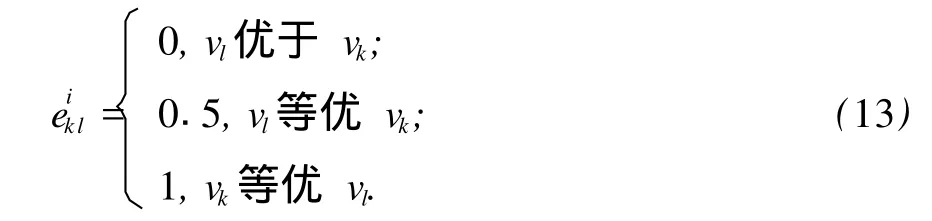
第 j个方案的指标特征值用 rij表示,则由 m个方案构成的对因素 ui的优越性排序一致性标度矩阵 Ei为

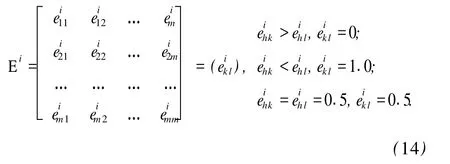
若不满足条件,则需重新判断,直到满足为止。根据 Ei各行和数从大到小进行排列,得到各设计方案在满足排序一致性条件下优越性的定性排序,其中标度为 0.5的两个方案,对应行的和数相等、重要性排序相同。在优越性定性排序的基础上,以排序第 1的方案为基准进行二元对比,得到各方案就因素 ui而言的相对隶属度 riij为

3.3 影响因素权重的计算

因素集 U={u1,u2,…,un}权重向量的确定类似于上述方法,对 n个因素的重要性做二元对比,给出重要性排序一致性标度矩阵,再根据重要性排序一致性标度矩阵各行和数大小进行排列,得到各影响因素在满足排序一致性条件下的重要性定性排序。在此基础上,建立语气算子与重要性定量标度之间的对应关系,得出评价指标因素集对重要性的相对隶属度向量,归一化后得到指标因素集的权重向量为

4 算例分析

4.1 有限元模型

以 200 m水深导管架平台为例,给出了 4种初始设计方案。图 1为相应的有限元计算模型。平台主体结构采用基于梁理论的管单元模拟,其中水中部分的单元通过Morrison方程考虑水动力效应的影响,上部组块质量简化为质量块,认为平台桩腿在泥面以下 6倍桩径处为固定端,坐标处为海平面高度。管节点处应力集中系数根据经验公式和有限元方法求得。图 1中 (a),(b)对应底部支撑部分由 4根主桩和 12根裙桩组成的方案;(c),(d)对应底部支撑部分由 8根主桩和 24根裙桩组成的方案。(a)与 (b),(c)与(d)之间的区别主要在于斜撑形式不同,(a),(c)主要是 X结构,(b),(d)主要为 X与K型的混合结构。

图 1 平台有限元计算模型Fig.1 Fin ite elementmodel of jacket platform

4.2 平台优化过程及结果分析

优化设计变量分别为柱腿及斜撑构件的外径D和壁厚 t。极限静力载荷优化设计时,约束条件包括强度约束(构件的最大正应力,最大剪应力符合规范要求)、稳定约束(受压构件的最大轴向稳定应力符合规范要求)、刚度约束(导管架顶部点侧位移最大值符合规范要求)、几何约束 (设计变量的下限和上限)以及桩基极限抗拔力约束。图 2为方案 (d)的设计变量位置示意图,参数范围见表 1。

采用一阶优化算法进行分析,在每次迭代中,采用梯度计算确定搜索方向,并用线性搜索法对非约束问题进行最小化。优化计算过程收敛后得到 8个可行的设计序列,然后将结构的一阶模态与疲劳可靠性指标作为约束条件进行结构动力优化设计。由于优化过程中整个平台形状不变,仅是构件尺寸发生变化,所以假设热点的位置在整个过程中保持不变。

针对每个设计序列,采用谱分析方法进行平台疲劳寿命可靠性分析。根据波浪统计资料[9],按照波浪方向可以划分为 8个工况,然后再以波浪的特征值划分为 76个子工况。波浪谱采用 ITTC谱,每个疲劳子工况的波浪谱由波浪统计特征值计算得到。由于每个方向的疲劳工况、波浪方向和水深是相同的,只有波高与周期的差别,故只须计算不同波浪方向工况下的应力传递函数[10]即可。各子工况下应力范围服从 Rayleigh分布,由公式 (2)求得由所有海况组成的长期应力参数Ω。由公式 (6)计算导管架平台各失效点的疲劳可靠性指标。计算过程中结构材料特性S-N曲线中参数m的值取为3.5,其他相关数据 ~Δ=1.0,~A=4.26×1013,~B=1.0,CΔ=0.3,CA=0.5,CB=0.25[11-12]。采用β-Unzipping法识别关键失效途径并求解结构系统疲劳失效概率,求出系统名义可靠性指标βs。图 3为方案(d)结构质量、一阶模态值以及疲劳可靠性指标在优化过程中的变化趋势。为了便于分析,将每一个设计序列下的变量值除以初始值。方案 (d)的设计变量优化结果列于表 1。

图 2 方案(d)的设计变量位置Fig.2 Design variables locations of scheme(d)

表 1 方案(d)设计变量优化结果Table 1 Opti mum results of design variables for scheme(d)

4种方案的导管架平台质量及系统可靠性指标优化结果列入表2中。

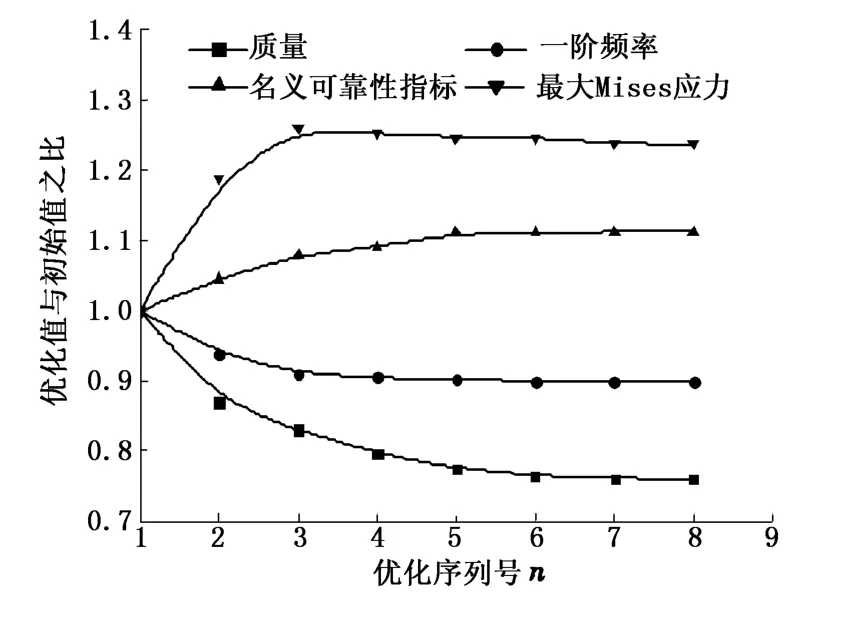
图 3 方案(d)的优化设计曲线Fig.3 Opti mum design curve of scheme(d)

表 2 导管架平台优化结果Table 2 Opti mum results of jacket platform

4.3 平台方案模糊优选

由优化设计部分得到平台质量、系统名义可靠性指标、平台承载力、平台顶部最大水平位移等结构参数,为模糊优选提供定量指标,减少了模糊因素,有利于做出合理的决策。对于深水导管架来说,随机波浪载荷作用下的疲劳可靠性问题是一项重要考察指标,因此其相对权重较高。根据三级模糊优选方法对优化后的各平台方案进行优选。

(1)一级模糊优选。权数集W1为

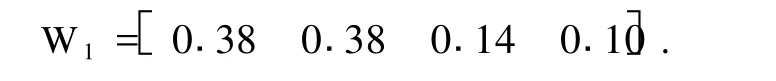
模糊相对隶属度矩阵 R1为

一级模糊优选结果B1为

(2)二级模糊优选。权数集W2为

模糊相对隶属度矩阵 R2为

二级模糊优选结果B2为

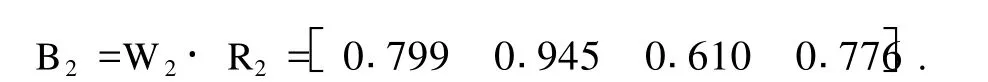
(3)三级模糊优选。权数集W3为

模糊相对隶属度矩阵 R3为

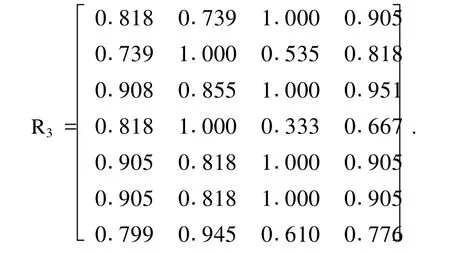
三级模糊优选结果B3为

由模糊优选结果可以看出,4种方案优选排序结果为(b)>(a)>(d)>(c)。为进行对比,按照初始方案结构性能进行模糊优选,其三级模糊优选结果为(b)>(d)>(a)>(c)。可以看出虽然最终的最优方案都是 (b),但是 (a)与 (d)的次序发生了变动,这是由于优化后的结构性能指标发生改变所致。因此,先对初始方案进行优化分析得到各型式下的最佳方案,然后进行模糊优选,得到的决策结果更为合理。

5 结束语

将基于谱分析法求得的疲劳可靠性指标作为约束条件进行优化,同时在模糊优选过程中也将疲劳可靠性作为一项重要考评指标,使深水导管架方案更加符合实际。进行平台方案的模糊优选之前,先由优化设计分析得到各初始方案的最优结构参数及性能指标作为模糊优选的定量化指标,减少了模糊因素,有利于对平台方案做出客观、正确的评价。4主桩和 12根裙桩的混合型结构为最优方案。

[1]翟刚军,封盛,康海贵,等.海洋平台设计选型的多级模糊优化及非结构性模糊决策分析[J].中国造船,2002, 43(1):23-28.

ZHA I Gang-jun,FENG Sheng,KANG Hai-gui,et al. Optimum lectotype of offshore platform based on multilevel fuzzy optimization and non-structural fuzzy decision [J].Shipbuilding of China,2002,43(1):23-28.

[2]桑松,李华军,董胜.交互式多目标决策方法及其在海洋平台方案综合优选中的应用 [J].船舶力学,2006,10 (4):54-59.

SANG Song,L IHua-jun,DONG Sheng.Interactive multiobjective decision-making method and its application in preferred marine platfor ms[J].Journal of Ship Mechanics,2006,10(4):54-59.

[3]L I Gong,L I U Xiang,L I U Yuan,et al.Optimum design of ice-resistant offshore jacket platforms in the Bohai Gulf in consideration of fatigue life of tubular joints[J].Ocean engineering,2008,35:184-493.

[4]W IRSCH I NG P H,L IGHTM C.Fatigue under wide band stresses[J].Journal of the Structural Division,1980(7): 1593-1607.

[5]W IRSCH I NG P H.Fatigue reliability for offshore structures [J].Journal of Structural Engineering,ASCE,1984,11 (10):2340-2355.

[6]HU Yu-ren,CHEN Bo-zhen.A first order second moment approach to systems fatigue reliability of offshore structures[J].OMAE,1993,2:327-334.

[7]李登峰,陈守煜.时序多目标决策的模糊优选法 [J].系统工程与电子技术,1994,16(3):13-17.

L IDeng-feng,CHEN Shou-yu.A fuzzy opti mum seeking method formultiple objective decision makingwith time series[J].Journal of Systems Engineering and Electronics, 1994,16(3):13-17.

[8]陈守煜,韩晓军.模糊集决策单元系统理论及其在黄河置换水量分配中应用[J].大连理工大学学报,2006,46 (1):98-102.

CHEN Shou-yu,HAN Xiao-jun.Unit systematic theory of fuzzy sets decision-making and its application to reallocation of replacedwaterof the Yellow River[J].Journalof Dalian University of Technology,2006,46(1):98-102.

[9]海洋图集编委会.南海海洋图集[M].北京:海洋出版社,2006.

[10]方华灿,陈国明.冰区海上结构物的可靠性分析[M].北京:石油工业出版社,2000.

[11]American Petroleum Institute.API recommended practice 2A-WSD(RP 2A-WSD)twenty-first edition[S]. Washington C:American Petroleum Institute,2000.

[12]DNV.Recommended practice RP-C203[S].Norway: DetNorske Veritas(DNV),2000.

(编辑 沈玉英)

Fuzzy lectotype of deep water jacket platform based on fatigue reliability opti m ization design

YANG Xiu-juan1,X IU Zong-xiang1,YAN Xiang-zhen1,FENG Yong-xun2
(1.College of Transport&Storage and Civil Engineering in China University of Petroleum,Dongying257061,China; 2.Shengli Engineering&Consulting Com pany Lim ited,Dongying257026,China)

The complicated system decision problem for design scheme optimization of deep water jacket platform was analyzed.The four initial design schemeswith different structure typeswere proposed.The optimal structure design parameters for each scheme were obtained by optimum design method,in which the nominal fatigue reliability index of structure system obtained by spectralmethod was taken as a key constraint condition.According to the optimized structural perfor mance parameters,the factorswhich had effects on the type selection of deep water jacket platform were comprehensively considered. The objective weight and relativemembership degree for each factorwere obtained by binary comparisonmethod.Finally,the three-level fuzzy optimum decision method was used for the fuzzy optimization.A deep water jacket platform for 200 m was taken as an example.The results show that the opti malperformance parametersobtained byoptimization analysisof initial design schemes can give accurate quantitative indexes and the fuzzy factors are reduced compared with the conventionalmethods.The method ismore beneficial to obtain the reasonable evaluation of deep water jacket platform.

deep water jacketplatform;optimum design;spectral analysis;three-level fuzzy optimization decision;fatigue reliability index

TE 54

A

10.3969/j.issn.1673-5005.2010.02.020

1673-5005(2010)02-0098-06

2009-08-29

中石化集团公司重点攻关项目(P08032)

杨秀娟(1957-),女(汉族),山东胶南人,教授,博士生导师,从事油气工程力学、机械强度及可靠性方面的教学和科研工作。