一类非齐次微分方程解的增长性

吕巍然,王君苓,陈院生,李晓静

(中国石油大学数学与计算科学学院,山东东营 257061)

一类非齐次微分方程解的增长性

吕巍然,王君苓,陈院生,李晓静

(中国石油大学数学与计算科学学院,山东东营 257061)

研究一类非齐次线性微分方程 f(k)+ak-1f(k-1)+…+a1f′-(eQ(z)-h0)f=1(k≥1)解的增长性,其中 aj(j=1,2,…,k-1)为常数,Q(z)为非常数多项式,h0为超越慢增长整函数。利用所得结果,还可以给出有关亚纯函数唯一性的结果。

微分方程;整函数;增长级;超级

1 问题的提出

本文中使用值分布理论的基本概念和标准记号[1-4]:用 T(r,f)表示亚纯函数 f(z)的特征函数,用m(r,f)表示 f(z)的均值函数等。特别地,用记号σ(f)和σ2(f)分别表示亚纯函数 f(z)的增长级和超级[4,5]。假设 f(z)和 g(z)是非常数亚纯函数,a为任意复数。如果 f(z)-a与 g(z)-a的零点相同,而且每个零点的重级也相同,则称 a为 f(z)与 g (z)的 CM公共值[4-6]。

对于集合 E⊂R+,用λ(E)表示 E的对数测度,用χE(t)表示集合 E在 R+上的特征函数,则可以定义集合 E的上对数密度和下对数密度如下:

考虑微分方程

的增长级问题,其中Q(z)是非常数多项式。

杨连中教授[7]证明了定理A。

定理 A 非齐次微分方程(1)的任意解必为无穷级整函数。

考察微分方程

不难发现方程(1)是方程(2)的特殊情况,本文中将继续研究方程(2)的解具有怎样的增长性。

对于 h0为常数的特殊情况,王珺曾给出有关方程解的增长性及其应用[6],并证明了如下结果:

定理 B 如果 h0为常数,则微分方程 (2)的任意非零解 f(z)满足σ(f)=1或σ(f)=∞,且任意具有无穷级的解其超级为不大于 degQ的正整数;

定理 1 如果 h0为超越慢增长整函数,则微分方程 (2)的任意非零解 f(z)满足σ(f)=∞。

把函数与其导数结合起来研究函数的唯一性,也是亚纯函数值分布论中一个重要的研究方向,且大多数仅仅涉及一阶导数或者 k阶导数[4]。本文中把相关结果推广到亚纯函数 f的线性微分多项式。

2 主要引理

引理 1[9]假设 g(z)是整函数,且级σ(g)= σ,vg(r)是 g的中心指标,那么

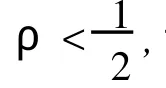
(i)如果δ(P,θ)>0,则

(ii)如果δ(P,θ)<0,则

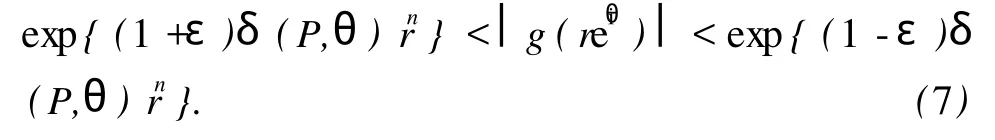
3 定理 1的证明

由线性微分方程的复振荡基本理论可知,方程(2)的所有解为增长级不小于 degQ的超越整函数。事实上,设 f(z)为方程 (2)的解,显然 f(z)为整函数,并且根据函数级的性质知道σ(f)≥σ(eQ)= degQ。对于方程 (2)的增长级不小于 1的解 f(z),下面将用反证法证明 f具有无穷增长级。首先假设σ(f)<∞。

改写(2)为

根据W iman-Valiron理论[9,12-13],可知

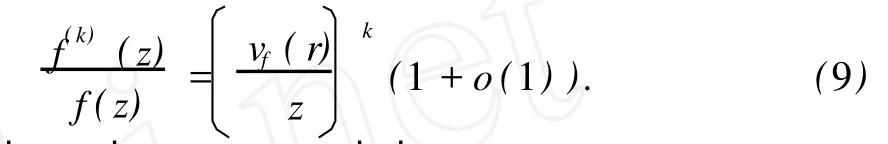
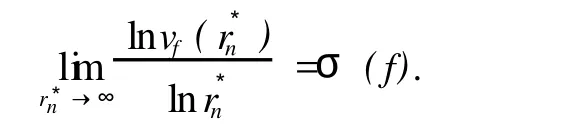
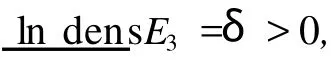
其中κ>0为常数。

由上极限和下极限的基本性质,有

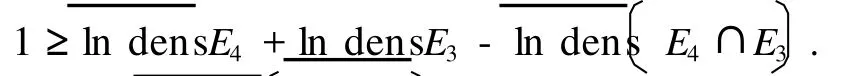
由此和式(9)可知,下式成立:

因为 f是超越整函数,易知M(r,f)→∞(r→∞).由此,将式 (9),(10)和 (13)代入式 (8),故可知当 n充分大时,有

这与 h0超越矛盾。从而可知存在 j0(1≤j0≤m),使得δj0(Q,θ0)≠0。可找到 j0使得满足 j>j0的 j,有δj(Q,θ0)≠0。那么存在两种情形:(i)δj0(Q,θ0)< 0;(ii)δj0(Q,θ0)>0。

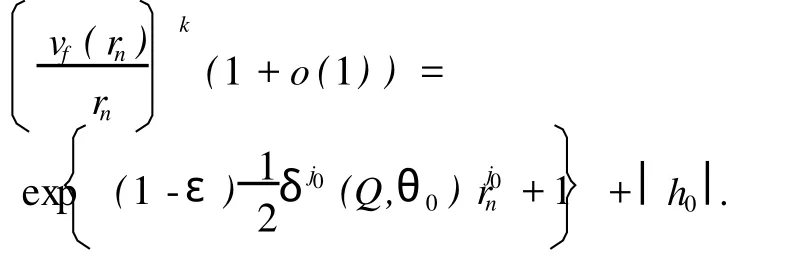
这与 h0超越矛盾。

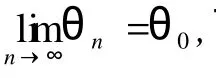
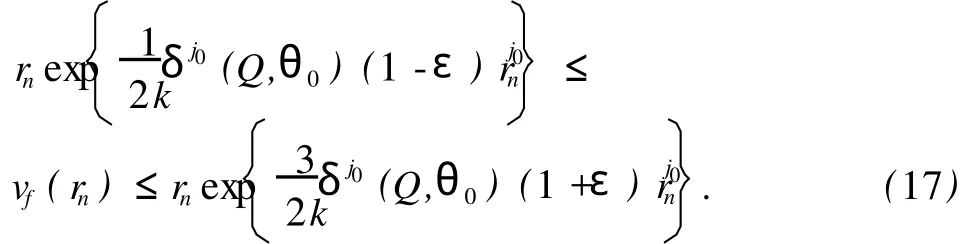
根据引理 2,式(17)显然与σ(f)<∞矛盾。

定理1证毕。

4 定理 2的证明

首先根据 CM公共值的定义和 Hadamard分解定理,有

其中Q(z)为多项式。假设 Q(z)不为常数,可将式(18)展开为式 (2),利用定理 1的结果得到σ(f)=∞与条件σ(f)<∞矛盾,所以Q(z)只可能为常数b。令 c=eb,定理 2证毕。

[1] HAY MAN W.Meromorphic function[M].Oxford:Clarendon Press,1964.

[2] LA I NE I.Nevanlinna theory and complex differential equation[M].Berlin:Walter de Gruyter,1993.

[3] 杨乐.值分布论及其新研究[M].北京:科学出版社, 1982.

[4] 仪洪勋,杨重骏.亚纯函数唯一性理论 [M].北京:科学出版社,1995.

[5] 吕巍然,王珺.具有三个公共值亚纯函数惟一性问题的注记 [J].石油大学学报:自然科学版,2004,28 (1):119-121.

LÜWei-ran,WANG Jun.Remarks on the problem of uniqueness ofmeromorphic functions sharing three values [J].Journal of the University of Petroleum,China(Edition ofNaturnal Science),2004,28(1):119-121.

[6] 张同对,吕巍然.涉及导数的亚纯函数的惟一性[J].中国石油大学学报:自然科学版,2007,31(6):130-134.

ZHANG Tong-dui,LÜWei-ran.On uniquenessof derivatives of meromorphic functions[J].Journal of China University of Petroleum (Edition of Naturnal Science), 2007,31(6):130-134.

[7] YANGL Z.Solutionsof a differential equation and its application[J].KodaiMath J,1999,22:458-464.

[8] 王珺.关于一类非齐次线性微分方程解的增长性及其应用[J].江西师范大学学报,2003,27(2):115-117.

WANG Jun.The growth of solutions of some non-homogeneous linear differential equations and its application [J].Journalof JiangxiNor malUniversity,2003,27(2): 115-117.

[9] VAL I RON G.Lectures on the General Theory of Integral Functions[M].New York:Chelsea,1949.

[10] BARRY P D.On a theorem ofBesicovitch[J].Quart J Math Oxford Ser,1963,14:293-302.

[11] CHEN Z X.The zero,pole and order of meromorphic solutions of differential equationswithmeromorphic coefficients[J].KodaiMath J,1996,19:341-354.

[12] HAY MAN W.The local growth of power series:a survey of the W iman-Valiron method[J].Canad Math Bull,1974,17:317-358.

[13] 何育赞,肖修治.代数体函数与常微分方程[M].北京:科学出版社,1988.

(编辑 修荣荣)

Growth of solutions of some non-homogeneous differential equations

LÜWei-ran,WANG Jun-ling,CHEN Yuan-sheng,L IXiao-jing
(College of M athem atics and Com putational Science in China University of Petroleum,Dongying257061,China)

The growth of solutions off(k)+ak-1f(k-1)+…+a1f′-(eQ(z)-h0)f=1(k≥1)withaj(j=1,2,…,k-1)constants is studied,whereQ(z)is a non-constant polynomial andh0is transcendental slowly growth entire function.The uniqueness ofmeromorphic functionswas obtained on basis of this.

differential equation;entire function;order;hyper order

O 174.5

A

10.3969/j.issn.1673-5005.2010.02.034

1673-5005(2010)02-0166-03

2009-02-10

吕巍然(1962-),男(汉族),山东沾化人,教授,博士,研究方向为复分析。