嵌入尺度可变均值漂移算法的粒子滤波方法
林渊灿,陈锻生,胡小平
(华侨大学计算机科学与技术学院,福建 泉州 362021)
嵌入尺度可变均值漂移算法的粒子滤波方法
林渊灿,陈锻生,胡小平
(华侨大学计算机科学与技术学院,福建 泉州 362021)
将尺度可变均值漂移算法嵌入到粒子的扩散过程中,引导粒子扩散到后验概率密度函数的高密度区,提出一种嵌入尺度可变均值漂移算法的粒子滤波跟踪方法.利用对数极坐标图像的尺度不变性,在粒子扩散过程中同时进行位置、尺度空间漂移.实验表明,该方法不仅能顺利跟踪非连续尺度变化目标,而且需要更少的粒子数.
粒子滤波;均值漂移算法;尺度可变;对数极坐标;目标跟踪
均值漂移算法(Mean-Shift,MS)[1]和粒子滤波(Particle Filter,PF)[2]是实时目标跟踪技术中广泛采用的两种方法.PF是一种非线性、参数化的目标跟踪方法,适用于非线性动态系统,能够跟踪部分遮挡,甚至完全遮挡的目标.MS具有简单、快速、强鲁棒性等特点,只在位置子空间内搜索最优目标估计值,不存在有效的核窗尺寸更新模型.当目标尺度发生变化时,特别是在目标放大的情况下[3],MS的跟踪效果很差.Maggio等[4]提出PF和MS结合的跟踪方法(简称HT).即将MS嵌入到PF的粒子扩散过程中,用MS指导粒子在位置子空间中进行漂移,使得扩散后的粒子群聚集在后验概率密度函数的高密度区,有效地减少粒子数;同时,它利用PF的状态转移模型对目标的尺寸进行预测,能够跟踪尺度连续变化的目标.但当目标进行非连续尺度变化时,HT的状态转移模型无法预测目标的尺度信息,导致跟踪失败.Han等[5]提出了一种尺度可变均值漂移算法(简称KBT-VRM).它通过对数极坐标变换[6],将目标尺度变换转换为在对数极坐标下的平移变换,使得目标的位置变化和尺度变化统一到MS算法框架中,实现对尺度变化目标的跟踪.与MS一样,KBT-VRM也无法跟踪有遮挡的目标.为解决该问题,本文提出一种嵌入尺度可变均值漂移算法的粒子滤波方法(简称PF-KBT-VRM).
1 状态转移模型
状态转移方程的形式对最终跟踪效果的影响很大.文中提出一种改进的自适应状态转移模型,以文[4]的状态转移模型为基础,加入前一时刻运动趋势信息项ΔSt-1.即

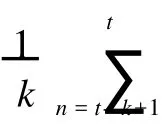
2 目标表示模型
假设用椭圆近似目标区域,t时刻的第i个候选区域表示为St,i=(x,y,hx,hy).其中:x,y为椭圆中心,hx,hy分别为横轴、纵轴的半轴长.一个候选区域的核直方图(B)可定义为
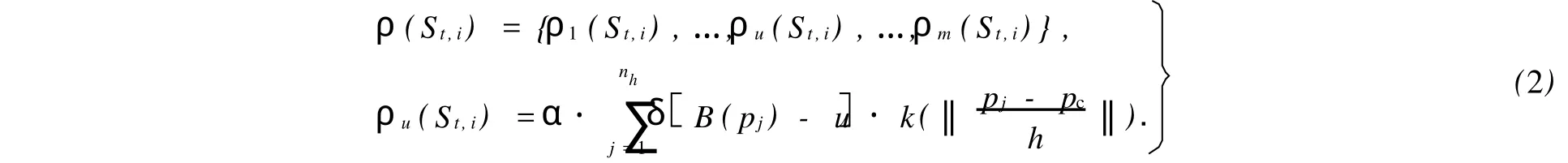
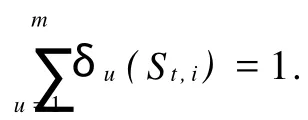
由于遮挡、背景干扰等因素,候选区域的边缘像素不太可靠,相应的权重值应该较小.一般选用中心区域权重较大,边缘区域权重较小的核函数,如高斯核或者Epanichnikov核等.后者的导数为一个常量,可以简化均值漂移向量的计算.因此,采用Epanichnikov核,其表达式为

候选区域与目标的相似度,用候选区域核直方图与目标核直方图之间的Bhattacharyya距离(DB)[7]来度量,则有

式(4)中:ρ为候选区域核直方图;q为目标区域的核直方图.由于光照变化、摄像角度、相机参数变化,以及目标进行非平面旋转等因素的影响,目标的外观会随着时间的推移会不断变化.为了反映目标外观的变化,采用文[8]的自适应目标表示模型,即
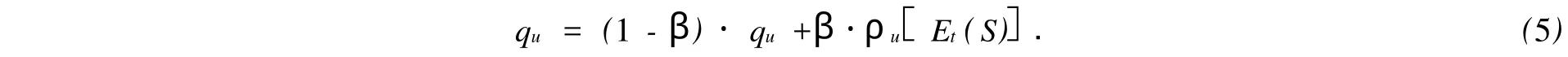
式(5)中:Et(S)为时刻t目标状态的估计值,β为遗忘系数.
这个自适应的目标模型实际上是一个遗忘过程.随着时间的推进,旧目标模型对新目标模型的影响越来越小.为了提高自适应目标模型的鲁棒性,避免在跟踪失败时进行模型更新,可以设置一个阈值PT,只有在当前帧状态估计值与目标的相似度大于PT时,才进行目标模型更新.
3 算法步骤
提出的算法的一次迭代过程,有以下5个步骤:(1)重采样;(2)根据式(1)进行状态转移;(3)对每个粒子进行尺度可变均值漂移;(4)计算每个粒子与目标的相似度,更新各个粒子的权重,计算当前帧的估计值;(5)更新目标表示模型.
实验中,各个参数设定:bt初始值为0.25,β值为0.01,PT为0.7,Ns为768,Nθ为576;HT的Nk和n(粒子数)分别为65,80;PF-KBT-VRM的Nk和n(粒子数)分别为20,15.
4 实验结果与分析
为了验证所提方法能够成功跟踪非连续尺度变化目标和有遮挡目标,分别在3个自拍的视频数据上进行实验.3个实验均选用具有视觉均匀特性的HMMD颜色空间.与MPEG-7相同,选取Hue,Sum,Diff 3个分量,各个分量的量化等级:Hue为18,Sum为8,Diff为4.在部分遮挡,甚至完全遮挡情况下,所提方法的跟踪结果如图1(a)所示.在目标进行非连续尺度变化时,所提方法和HT方法的跟踪结果,如图1(b),(c)所示.图1(b),(c)中:上、下视频分别为HT和PF-KBT-VRM的跟踪结果;图1(b),(c)的视频分别是在白天和晚上拍摄的,目标的尺寸刚开始保持不变,接着目标的尺寸不断增大.

图1 视频跟踪结果比较Fig.1 Comparison of video face tracking
从图1(b),(c)可以看出,在目标尺寸不变的情况下,所提出的PF-KBT-VRM跟踪算法和文[4]中的HT方法都能够成功跟踪.然而,在目标尺寸突然变大的非连续变化情况下,HT方法出现跟踪失败,而PF-KBT-VRM仍然能够正常跟踪,如图1(b)中的帧编号206的视频和图1(c)中帧编号115,123,131的视频所示.
PF-KBT-VRM和HT两种方法在视频2,3上各自跟踪结果与真实目标的相似度曲线,如图2所示.图2中:n为视频帧编号;DB为跟踪结果核直方图与目标核直方图的Bhattacharyya距离.从图2可以看出,在目标尺寸不变时,两种跟踪方法的性能很接近;然而,在目标尺寸突然变大的非连续变化情况下,HT方法的跟踪性能明显低于提出的PF-KBT-VRM方法的跟踪性能.
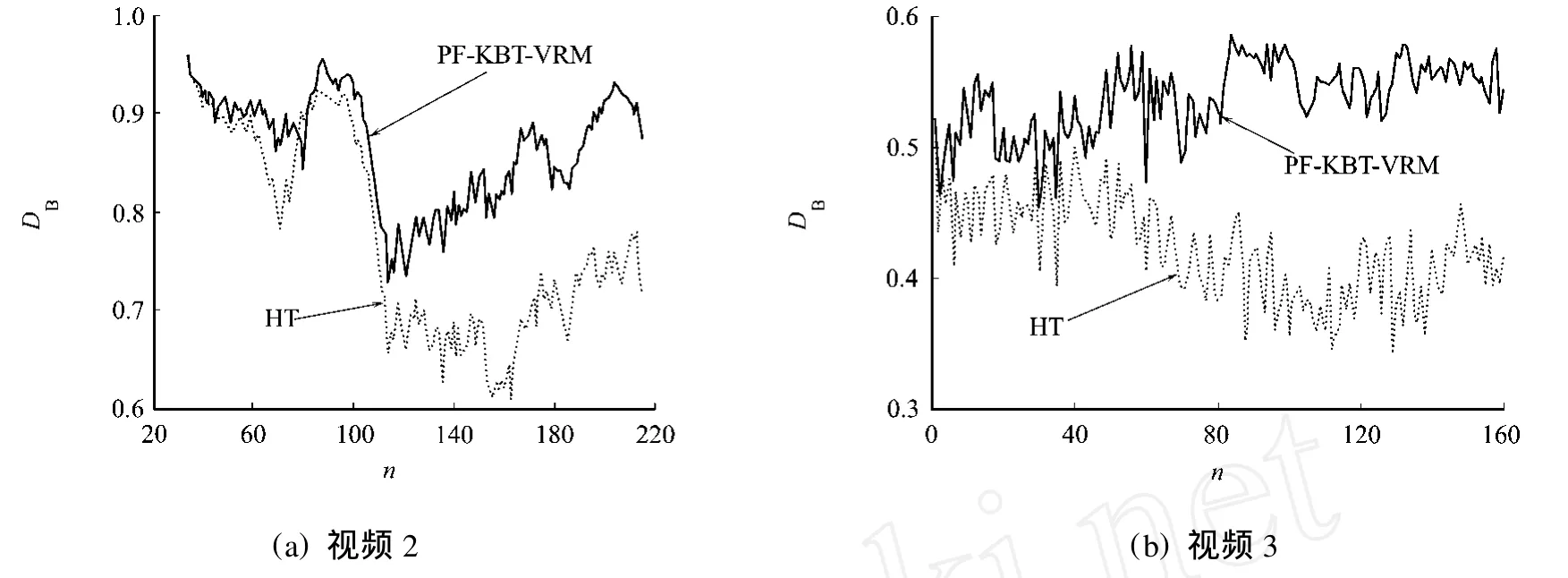
图2 跟踪结果与真实目标状态的相似度曲线Fig.2 Similarity curves of object tracking and their real states
视频2,3的粒子群尺寸分布的方差,如图3所示.图3中:横轴为帧编号(n),纵轴为当前帧所有粒子横轴半轴长的方差(σ).从图3可知,刚开始一段时间内,目标的尺寸保持不变,使得状态转移模型中的和变量趋于零.也就是说,粒子经过状态转移后,尺寸基本没变,而加上粒子滤波中的重采样过程,粒子群将发生“退化”现象,所有粒子的尺寸基本一致.因此,在视频2,3中,当目标的尺寸突然变大时,所有粒子的尺寸依然保持不变且基本等于上一帧目标的尺寸,从而导致跟踪的失败.

图3 粒子群尺寸分布的方差Fig.3 Variance of particle scales
从图3可以看出,在目标尺寸保持不变一段时间后,所有粒子尺寸的方差趋于零,即各个粒子的尺寸基本一样.提出的PF-KBT-VRM方法嵌入的是具有尺度变化能力的MS方法,因此,在状态转移模型无法预测目标尺寸的情况下,各个粒子仍然能够自适应地更新各自的窗宽,实现对非连续尺度变化目标的有效跟踪.
5 结论
粒子滤波跟踪结果的尺寸取决于粒子群的尺寸分布.在正常情况下,粒子群的尺寸在整个尺寸空间中随机分布.为了使得跟踪结果的尺寸接近于真实目标的尺寸,除了给接近真实目标尺寸的粒子赋以更高的权重外,还应该使得尽可能多的粒子分布在真实目标尺寸附近.如果粒子数目越多,那么分布在真实目标尺寸附近的粒子数也就越多,最后跟踪结果的尺寸也越接近于真实尺寸.这也就是在一般情况下粒子数目越多,粒子滤波跟踪效果越好的原因.
在HT方法中,由于嵌入的是传统的MS算法,因此在粒子漂移过程中,MS算法不能够指导粒子漂向真实目标尺寸的周围.PF-KBT-VRM方法中,由于嵌入的是尺度可变的MS算法,在粒子漂移过程中,尺度可变MS算法不仅在位置空间上进行漂移,同时也在尺度空间上进行漂移,能够指导大部分粒子漂向真实目标尺寸附近.因此,虽然所提方法在3个实验中均只采用20个粒子,而HT方法却采用了80个粒子,由于尺度可变MS算法的指导,PF-KBT-VRM中的大部分粒子分布在真实目标尺寸附近,使得PF-KBT-VRM在使用更少粒子的情况下反而取得比HT更好的跟踪结果.
提出的跟踪方法假设目标的外观变化在帧与帧之间比较轻微,传统均值漂移算法和嵌入传统均值漂移算法的粒子滤波方法同样也必须在这个前提下才能有效地跟踪目标.该假设前提大大缩小了提出方法的适用范围.在下一步的工作中,将进一步研究如何有效地更新目标表观模型,实现对旋转目标、明显表观变化目标的跟踪.
[1]COMANICIU D,RAMESH V,MEER P.Kernel-based object tracking[J].Pattern Analysis and Machine Intelligence,2003,25(5):564-577.
[2]ISARD M,BLAKE A.Condensation:Conditional density propagation for visual tracking[J].International Journal of Computer Vision,1998,29(1):5-28.
[3]PENG Ning-song,YANGJie,LIU Zhi.Performance analysis for tracking of variable scale objects using mean-shift algorithm[J].Optical Engineering,2005,44(7):070505.
[4]MAGGIO E,CAVALLARO A.Hybrid particle filter and mean shift tracker with adaptive transition model[C]//IEEE Signal Processing Society International Conference on Acoustics,Speech,and Signal Processing.Philadelphia:IEEE,2005:19-23.
[5]HAN R,J ING Z,LI Y.Kernel based visual tracking with variant spatial resolution model[J].Electronics Letters,2008,44(8):517-518.
[6]SCHWARTZ E L.Anatomical and physiological correlates of visual computation from striate to infero-temporal cortex[J].IEEE Transactions on Systems,Man and Cybernetics,1984,14(2):257-271.
[7]KAILATH T.The divergence and bhattacharyya distance measures in signal delection[J].IEEE Transactions on Communication Technology,1967,15(1):52-60.
[8]NUMMIARO K,KOLL ER-MEIERB E,VAN GOOL L.An adaptive color-based particle filter[J].Image and Vision Computing,2003,22(1):99-110.
[9]张波.基于粒子滤波的图像跟踪算法研究[D].上海:上海交通大学,2007.
A Particle Filter Method Embedded with a Variable Scale Mean-Shift Algorithm
LIN Yuan-can,CHEN Duan-sheng,HU Xiao-ping
(College of Computer Science and Technology,Huaqiao University,Quanzhou 362021,China)
Embedding variable scale mean-shift algorithm into particle diffusion process,particles are diffusion into the high density area of the post probability density function,this paper proposed a particle filter tracking method embedded with a variable scale mean-shift algorithm.The scale invariable characters of image in logarithmic polar coordinates was used in the particle diffusion process,in which position space and scale space are shifted at the same time.The experiment shows the method can not only track object smoothly with discontinuous scale variation,but also need less particles.
particle filter;mean-shift;variable scale;logarithmic polar coordinate;object tracking
TP 391.41
A
1000-5013(2010)04-0408-05
(责任编辑:鲁斌 英文审校:吴逢铁)
2009-05-19
陈锻生(1959-),男,教授,主要从事图像处理与计算机视觉的研究.E-mail:dschen@hqu.edu.cn.
福建省科技计划重点项目(2008I0021);福建省自然科学基金计划资助项目(2009J01289)

