时域多分辨小波的交替隐式差分方法

汤炜

（华侨大学信息科学与工程学院，福建 泉州 362021）

时域多分辨小波的交替隐式差分方法

汤炜

（华侨大学信息科学与工程学院，福建 泉州 362021）

采用Harr尺度和小波函数为空间场量展开函数，得到时域多分辨小波（MRTD）步进方程，并与交替隐式差分（ADI-FDTD）结合，导出ADI-MRTD融合步进方程.场量迭代的核心转化为分块三对角矩阵线性方程组，提出广义追赶法进行高效求解，讨论连接边界条件的处理，使该方法能够有效地模拟散射问题.以一维问题为例，验证ADI-MRTD融合技术的计算精度和有效性.

Harr尺度；小波函数；时域多分辨；交替隐式差分

时域有限差分（FDTD）方法已广泛应用于天线、散射和电磁兼容等问题的模拟与分析［1-2］.FDTD方法受CFL（Courant-Friedich-Lecy）稳定性和空间色散条件的限制，时间和空间步长均不能选取太大，使得该方法存在计算效率不高的缺陷.因此，有些融合其他技术的新方法，如伪谱时域差分方法（PSTD）［3-4］、时域多分辨小波（MRTD）［5-6］及交替隐式差分方法（ADI-FDTD）［7-8］等被相继提出.PSTD和MRTD是通过优化空间色散关系提高空间采样率，而ADI-FDTD时间色散关系则是与时间步长非相关的.MRTD灵活的空间抽样，使其和ADI-FDTD结合，使得改善空间分辨率和减小运算量成为可能.Chen等［9］最早提出这一思想，从理论上对其稳定性给予证明，并通过谐振腔模分量结果给出相对误差.王丽华等［10］利用Daubechies基重新推导时间无关的稳定性证明.相比对MRTD和ADI-MRTD的研究，这一混合方法迄今仍然没有取得较大的进展.本文采用Harr尺度和小波函数作为空间场量的展开函数，得到矩阵形式的MRTD步进方程，结合ADI-FDTD方法并导出ADI-MRTD方法步进方程.

1 基于Harr小波的MRTD方程

采用Harr尺度函数和小波函数作为空间场量的展开函数，可将MRTD方程改写为［9］

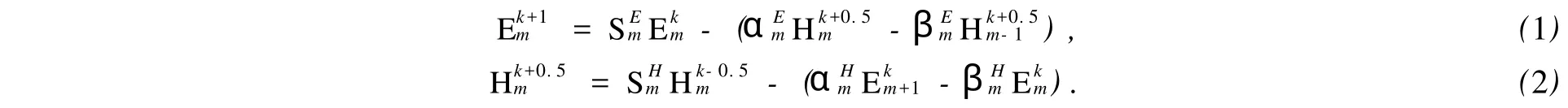
2 ADI-FDTD和MRTD融合技术

利用一维ADI-FDTD方程［12］，与式（1），（2）相结合，整理可分别得到如下2个时间分步.

（1）第1时间分步：

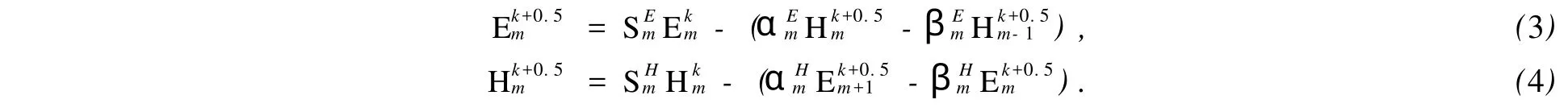
（2）第2时间分步：

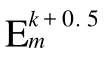
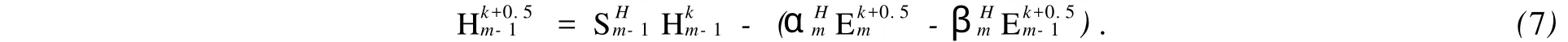
与式（4）一起代入式（3），消去时刻磁场分量，可得

设矩阵方程MX=V，其中M为三对角矩阵，则有

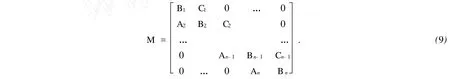
式（9）中：Ai，Bi，Ci均为m阶方阵，采用Harr小波基时，m=2.矩阵M通过LU分解，可以得到

其中，b1=B1，ck=b1-1Ck，bk+1=Bk+1-Ak+1ck，k=1，2，…，n-1.此时，原方程等价于Ly=V和Ux=y.采用广义追赶法求解，即广义追过程为

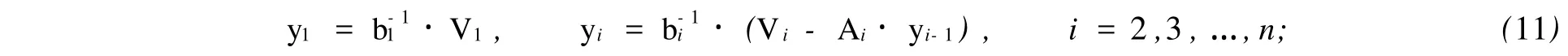
而广义赶过程为

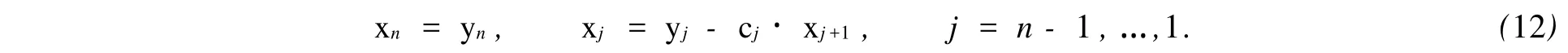
式（11），（12）中出现了矩阵求逆，由于分块矩阵均为2阶方阵，求逆过程并不会占用太多计算时间.

4个连接边界条件中，Ncmin，Ncmax分别代表右、左连接边界点；入射波场量（Einc和Hinc）为列向量，其元素分别为相应位置和时间上入射波的Harr尺度函数和小波函数分量.

3 数值算例

定义CFL约束条件参量αCFL=cΔt/Δs（c为自由空间光速），一维FDTD方法约束条件要求αCFL＜1，选用入射波为时域高斯脉冲，以提取结构的频域特性.

例1 无耗介质板的反射系数（ρR）和透射系数（ρT）.介质板厚度d=9cm，介电常数εr=4.选取ADI-MRTD空间步长Δs=1.5mm，时间步长Δt通过αCFL定义来设定，例1选择αCFL=5.介质板反射系数和透射系数数值结果与解析解的对比，结果如图1（a）所示.结果表明，当设定的αCFL参数远远超过FDTD的约束条件，也即时间步长远超过FDTD的取值范围，与解析方法的计算结果相比，在0～5GHz范围内几乎重合.由此可以看到，该方法对这类无耗媒质的适用性.

例2 有耗介质板的反射和透射系数.介质板厚度同例1，介电参数为εr=2σ，=0.01s·m-1.ADIMRTD的计算参数选取与例1相同，反射系数和透射系数的数值结果与解析解之间的对比，结果如图1（b）所示.与无耗介质板相比，有耗介质平板的反射系统随频率增加呈减小趋势，透射系数在0～5GHz范围内基本保持不变.对比算例1可以看到，介质对电磁波的吸收作用.

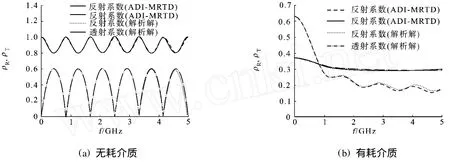
图1 反射系数和透射系数随频率的变化Fig.1 Reflection and transmission coefficient changes with the frequency

例3 一维光带隙（PBG）结构的频率响应.一维PBG结构由两种无耗媒质构成，如图2所示.图2中，媒质1（深色）介电常数εr，1=9，共有7层且每层厚度d1=7.5cm；媒质2（浅色）介电常数εr，2=1，与媒质1相间排列，厚度d2=22.5cm.采用ADI-MRTD和FDTD方法，对该PBG结构的频率响应进行数值模拟，结果如图3所示.图3中，FDTD的空间步长Δs=3.75mm，αCFL=0.5；ADIMRTD的空间步长与FDTD相同而αCFL=5.

图2 一维光带隙结构示意图Fig.2 Schematic one-dimensional photonicbandgap structure

计算结果表明，结构在250～450MHz频段内，入射波被PBG结构反射，传输系数趋于0，使得该结构对250～450MHz的电波形成传输禁带.图1（a），（b）和图3的结果表明，ADIFDTD和MRTD融合技术具有较高的计算精度.这种计算精度是在αCFL=5条件下得到的，是传统FDTD约束条件（αCFL=0.5）的10倍.也即是说，在相同计算资源情况下，ADI-MRTD运行时间步数仅为传统FDTD的1/10，有效地提高了计算效率.

虽然ADI技术使得迭代与时间步长无关，但仍依据计算频带最高频率与时间抽样频率的关系，即时间抽样必须满足Nyquist抽样频率［13］.同时，与传统的FDTD，MRTD和ADIFDTD方法相比，ADI-MRTD方法的编程复杂程度有了很大的增加.究其原因在于，ADI-MRTD方法中步进方程参量都是以矩阵形式出现的.

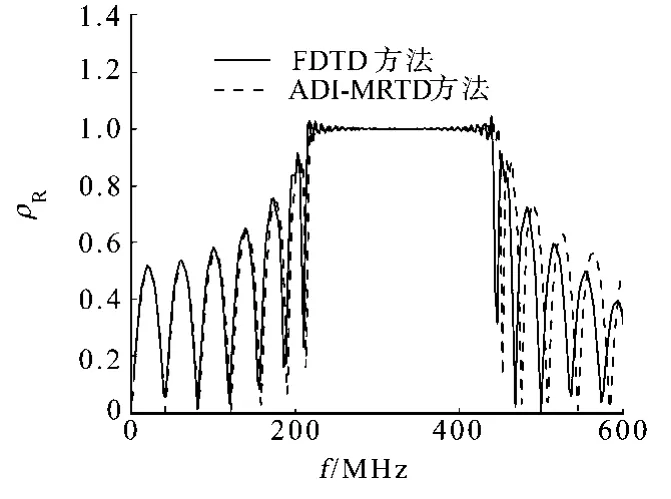
图3 PBG的反射系数随频率的响应Fig.3 Photonicbandgap of the reflection coefficient with frequency response

4 结束语

ADI-FDTD和MRTD融合技术保持ADI-FDTD无条件稳定性的同时，继承了MRTD解决多尺度电磁问题的优点.该技术可以推广到二维和三维情况，如模拟粗糙表面目标散射问题.只是在二维和三维问题中，无论吸收边界还是连接边界条件，处理过程都比较复杂.

参考文献：

［1］TAFLOVE A，HAGNESS S C.Computational electrodynamics：The finite-difference time-domain method［M］.London：Artech House，2000.

［2］汤炜，李清亮，吴振森.有耗平面和三维目标复合散射FDTD分析［J］.电波科学学报，2004，19（4）：38-443.

［3］LIU Q H.The PSTD algorithm：A Time-domain method requiring only two cells per wavelength［J］.Micro and Opt Tech Lett，1997，15（3）：158-165.

［4］LI Q L，CHEN Y C.Application of the PSTD for scattering analysis［J］.IEEE Transactions on Antennas and Propagation，2002，50（9）：1317-1319.

［5］KRUMPHOLZ M，KATEHI L.MRTD：New time-domain schemes based on multireslution analysis［J］.IEEE Transactions on Microwave Theory and Techniques，1996，44（4）：555-571.

［6］DOGARU T，CARIN L.Multire solution time-domain using CDF biorthogonal wavelets［J］.IEEE Transactions on Microwave Theory and Techniques，2001，49（5）：902-912.

［7］NAMIKI T.A new FDTD algorithm based on alternating-direction implicit method［J］.IEEE Transactions on Microwave Theory and Techniques，1999，47（10）：2003-2007.

［8］NAMIKI T.3-D ADI-FDTD method-unconditionally stable time-domain algorithm for solving full vector maxwell’s equations［J］.IEEE Transactions on Antennas and Propagation，2000，48（10）：1743-1748.

［9］CHEN Z Z，ZHANGJ Z.An unconditionally stable 3-D ADI-MRTD method free of the CFL stability condition［J］.IEEE Micro Wire Comp Lett，2001，11（8）：349-351.

［10］王丽华，吴先良.ADI-MRTD算法的数值色散性分析［J］.现代电子技术，2007，30（11）：17-20.

［11］DOGARU T，CARIN L.Application of Harr-wavelet-based multiresolution time-domain schemes to electromagnetic scattering problems［J］.IEEE Transactions on Antennas and Propagation，2002，50（6）：774-784.

［12］汤炜，焦培南，李清亮，等.ADI-FDTD方法在一维PBG结构中的应用［J］.电波科学学报，2003，18（3）：281-285.

［13］汤炜.ADI-FDTD及其混合算法在电磁散射中的应用［D］.西安：西安电子科技大学，2005.

Analysis of the Alternative Direction Implicit Method Based on Multi-Resolution Time-Domain

TAN G Wei
（College of Information Science and Engineering，Huaqiao University，Quanzhou 362021，China）

The paper derives the multi-resolution time-domain（MRTD）update equations adopting the Harr scaling and wavelet function as the expanding basis in space domain.The ADI-MRTD formulae are obtained by combining with the alternative-direction implicit/finite difference time-domain（ADI-FDTD）method.Due to the simplification of Harr wavelet，the field components in ADI-MRTD equation can be updated by the blocked tridiagonal linear equation，which can be evaluated by generalized tridiagonal equation method efficiently.Moreover，this paper discusses the adjacent boundary condition to simulation electromagnetic scattering.Finally，the proposed method is validated by some one-dimension numerical examples.

Harr scaling；wavelet function；multi-solution time-domain；alternative-direction implicit/finite difference time-domain

O 241；TN 011

A

1000-5013（2010）04-0404-04

（责任编辑：鲁斌 英文审校：吴逢铁）

2008-09-28

汤炜（1974-），男，副教授，主要从事电磁场数值算法的研究.E-mail：tangwei74@hqu.edu.cn.

华侨大学高层次人才科研启动项目（08BS411）