基于定数截尾数据指数分布参数的最短区间估计

王玉芳

（荆楚理工学院 数理学院，湖北 荆门 448000）

基于定数截尾数据指数分布参数的最短区间估计

王玉芳

（荆楚理工学院 数理学院，湖北 荆门 448000）

根据定数截尾数据，给出了参数的常用区间估计和最短区间估计，另外，还介绍了最短区间估计的求法。

定数截尾数据；指数分布；最短区间估计

1 引言

指数分布是寿命试验中常见的分布之一，其重要性首先在于，现实中许多样本的寿命都服从指数分布；其次，由于它的参数的点估计和区间估计易于得到，并且由指数分布可以派生出Γ分布、x2分布、F分布，这些分布的统计理论较为成熟。本文首先给出定数截尾试验下人们较为熟悉的关于参数的区间估计，最后讨论了最短区间估计问题。

2 参数的极大似然估计和区间估计

设总体T服从参数为λ的指数分布，其密度函数为：

从服从该指数分布的一批产品中任取n个产品进行寿命试验，试验进行到事先规定的失效数时停止r(r≥），设其先后失效时间为t1≤t2≤…≤tr，其余n-r个在试验停止时刻tr尚未失效，由此所得到的就是定数截尾样本。

由此试验可得如下引理:

引理1：设t1,t2,…,tr是由n个试验样品的截尾数为r的定数截尾样本，则总试验时间T*r=t1+…+tr+(n-r)tr服从Γ （r,λ）分布，即T*r的概率密度函数为：

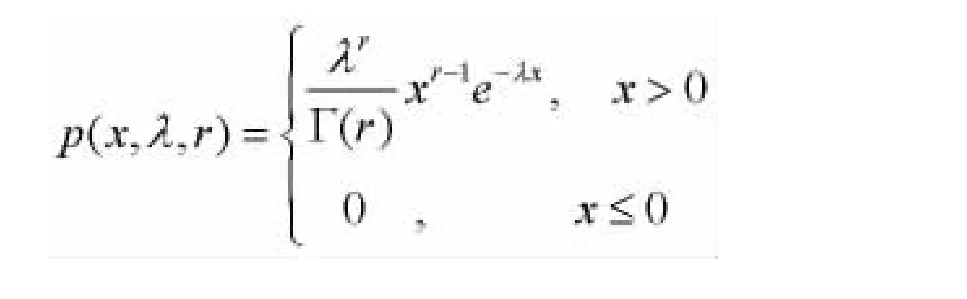
由引理1可得

引理2：随机变量2λT*r 服从自由度为2r的x2分布，即有2λ(2r)由引理2可得到2λ的概率密度函数为

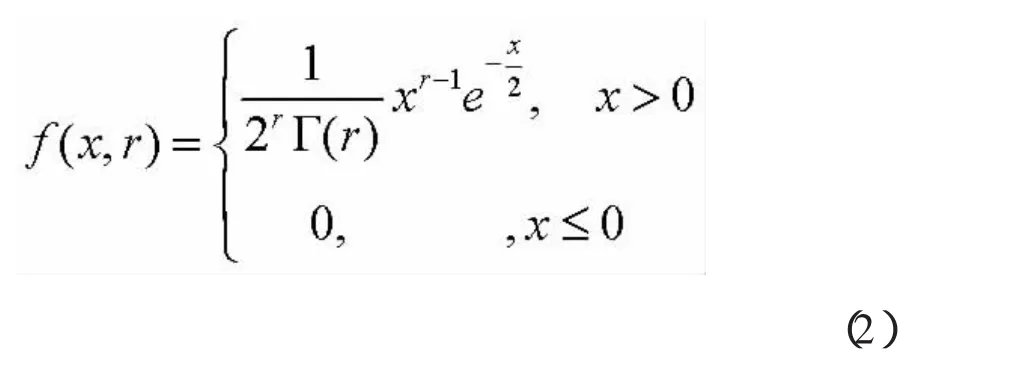
引理1和引理2的证明见文献 ［1］。

因此，由引理2对于给定的显著性水平α∈ （0，1），

由此可得

在产品的寿命服从指数分布 （1）的定数截尾试验中，参数λ的置信度为1－α的置信区间为

推论 关于参数λ的统计假设检验问题：

原假设 H0∶λ＝λ0，备择假设 H1∶λ≠λ0，

其中，λ0是某事先给定的常数。取统计量T＝2λ0T*r，则在给定的显著性水平α∈ （0，1） 下，当时，接收原假设时，拒绝原假设H0而接受备择假设H1。

由于x2分布的分位数有专用的x2分布表可查，使用起来比较方便，因此 （3）也是λ的常用区间估计，但是 （3）并不是λ的最短区间估计，下面将讨论λ的最短区间估计问题。

3 最短区间估计

对指数分布的参数λ作区间估计时，在固定的置信度下，我们一般认为置信区间越短越好。对于第二节推导出的λ的区间估计，由于随机变量2λ服从x2(2r)分布，它的密度函数 （2）不是关于峰值对称，所得到的置信区间

对给定的置信度1－α，设x1x2满足下式 不是最短的。

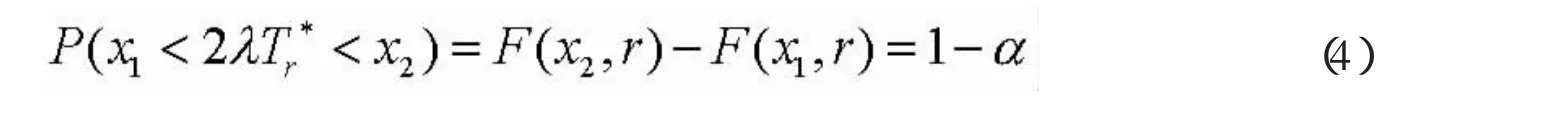
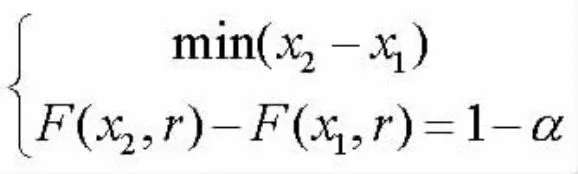
要解决上述条件极值问题，其显示解很难得到，因此我们先证明该条件极值的驻点是唯一存在的。

命题：当r≥2时，上述条件极值有唯一驻点。

证明：由拉格朗日乘子法，令

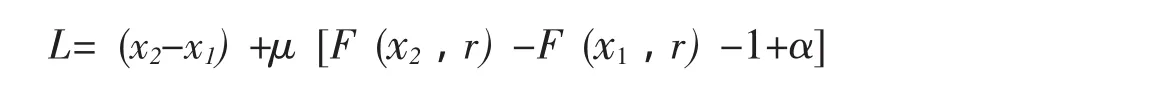
对x1，x2求偏导且令偏导为零，得

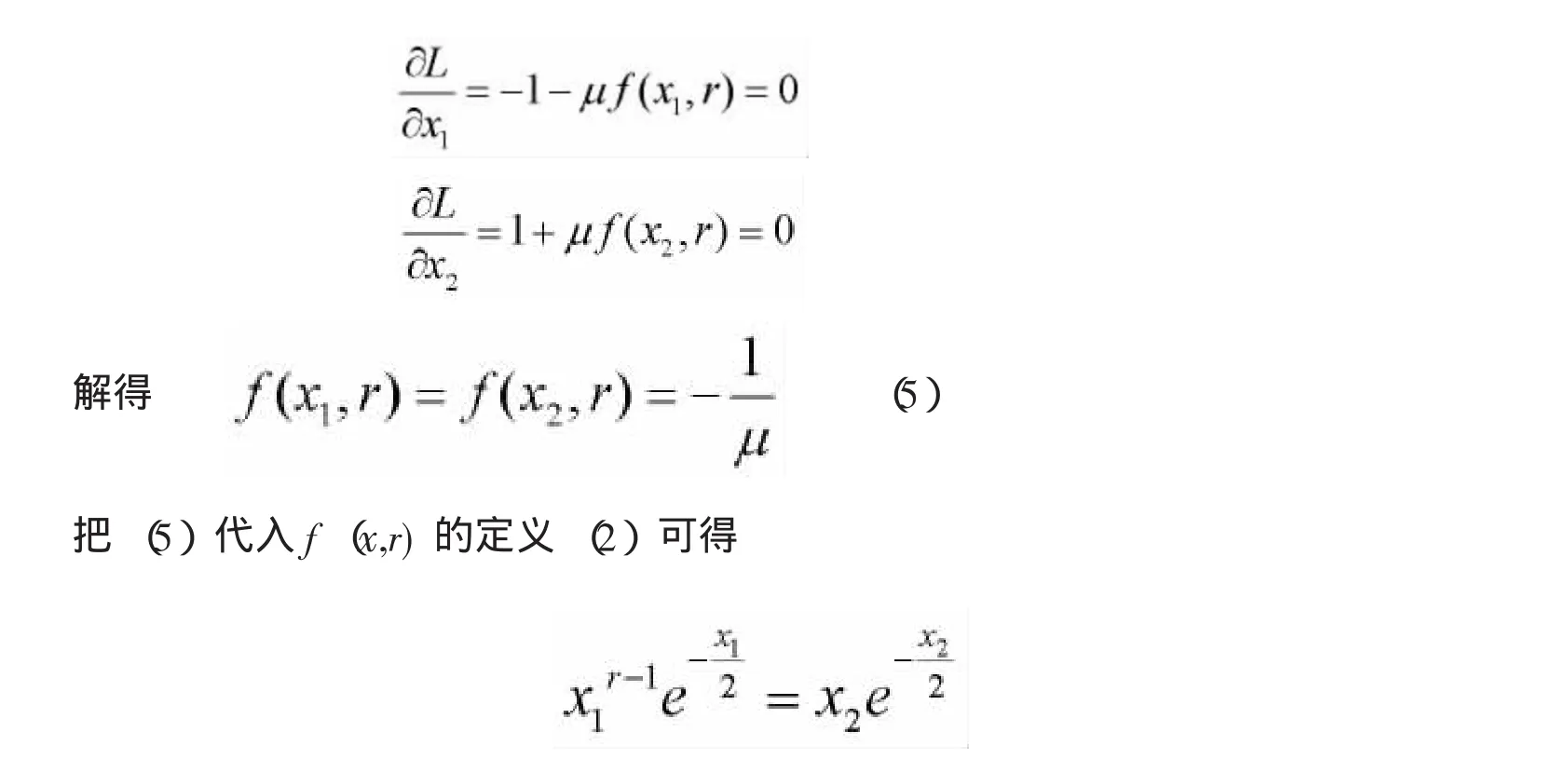
所求驻点 (x1-x2)就是（4）式与（6）式的解。这样，仅需证明（4）式与（6）式有解而且解是唯一的。令

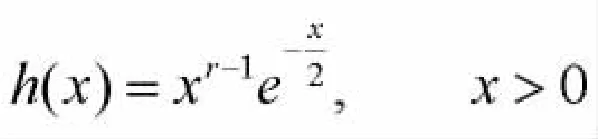
由 h′(x)=0，可得唯一稳定点 x0=2r-2；且当 x≤x0时，h′(x)≥0,h(x)严格单调递增，当 x≥x0时，h′(x)≤0,h(x)严格单调递减，因此x0=2r-2是h(x)的最大值点；而当x趋于正无穷大或零时h(x)趋于零。为保证x1＜x2和（6）式成立，应有 x1＜2r-2，x2＞2r-2。这样由任意 x2可唯一地解出 x1=u(x2)。

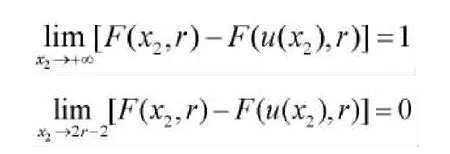
对于r≥2时，最短置信区间的求法可用MATLAB软件求得。

由区间估计和假设检验的关系，根据最短区间估计也可类似上述推论给出双边假设检验问题，这里不再列出。

[1]劳立斯（Lawless.J.F）.寿命数据中的统计模型与方法[M].茆诗松，译.北京：中国统计出版社，1998.

[2]茆诗松，王静龙，濮晓龙.高等数理统计[M].北京：高等教育出版社，1997.

[3]顾嘉麟，郭建英.截尾数据下威布尔分布的参数估计问题[J].哈尔滨理工大学学报，2005，10（2）：61-63.

[4]茆诗松，王玲玲.可靠性统计[M].上海：华东师范大学出版社，1984.

O212.2

A

1673-8535(2010)03-0015-04

王玉芳 (1976-)，女，湖北天门市人，荆楚理工学院数理学院讲师，硕士研究生，研究方向：概率统计。

（责任编辑：钟世华）

2009-10-22