期权的风险管理模型VaR最优解的静态探讨

骆文辉，李连芬

（1.江门职业技术学院 教育与教育技术系，广东 江门 529090；2.梧州学院 数理系，广西 梧州 543002）

期权的风险管理模型VaR最优解的静态探讨

骆文辉1，李连芬2

（1.江门职业技术学院 教育与教育技术系，广东 江门 529090；2.梧州学院 数理系，广西 梧州 543002）

期权的风险管理模型VaR是金融风险管理市场风险测量的一种方法。就期权定价模型,在VaR约束下的期权风险管理进行静态经济分析，从而探讨期权风险管理的最优的解。

VaR；期权；最优解；静态分析

在期权交易市场上不仅存在回避风险的套期保值者，而且更多的是投机者和套利交易者，当期权等衍生工具不能正确定价时，特别是对其价格变动不能正确预测时，投机者便有更多获利机会，或当不同交易所、不同交易商和做市以相同期权报价有差值时，则给套利者提供无风险套利机会。由此可见，如何对期权等衍生工具正确定价，以抑制过度投机活动，对降低金融市场波动风险具有重要意义。

1 期权定价公式的因素分析

期权就是持有者在为了某一特定时间或未来某一特定时间内以特定的价格购买或出售某一金融资产的权利。在到期日前，期权的价值依赖于它最后处于实值状态的概率和执行数量。标的期货价格上涨，看涨期权价格上涨，看跌期权价格下跌。标的期货价格下跌，看涨期权价格下跌，看跌期权价格上涨。这一现象可以直观地由看涨期权和看跌期权的定价公式得出：[1]

当标的资产价格的波动率为常数时，衍生证券的价值可以是标的资产价格S和时间T的函数，用Delat和Gamma表示衍生证券价值的资产价格变化的一阶、二阶导数，同时也表示了衍生证券价值以标的资产价格变化的线性和非线性风险衡量即灵敏度。用Vega和Theta表示衍生证券价值对标的资产价格波动性和时间的灵敏度。另外衍生证券的价值也会受到利率变化的影响，对利率变化的灵敏度用Rho表示。下面针对不同种类的衍生证券，分别介绍测量灵敏度的Delat、Gamma、Vega、Theta、Rho等。[1]

Delat是衍生证券的价格相对于其标的资产价格变化的比率，即衍生证券对其标的资产价格的线性或一阶灵敏度。在度量期权的灵敏度时，通过对B-S公式中的标的资产取一阶偏导数，可以得到看涨期权和看跌期权的Delat值：

例：假定标的资产的价格St=18，执行价格X=15，无风险利率r=10%，到期期限T=0.25，标的资产价格的波动性σ＝15%，则

Gamma是衍生证券的Delat变化相对于标的资产价格变化的比率，是衍生证券的价格对标的资产价格的二阶导数，它反映了衍生证券价格对标的资产价格的敏感性，基于不支付红利股票的欧式看涨期权或看跌期权的Gamma为：

一般来说Gamma值越大，期权的灵敏度也就越大。对于支付连续红利的股票看涨或看跌期权有：

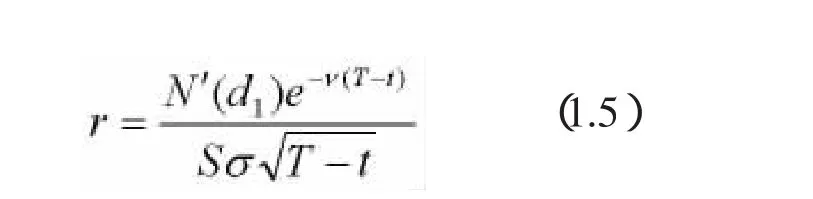
当V为外汇的无风险利率时，上式即为外汇欧式期权的Gamma公式；当V取无风险利率r、S为期货价格F时，上式就是欧式期货期权的Gamma计算公式。

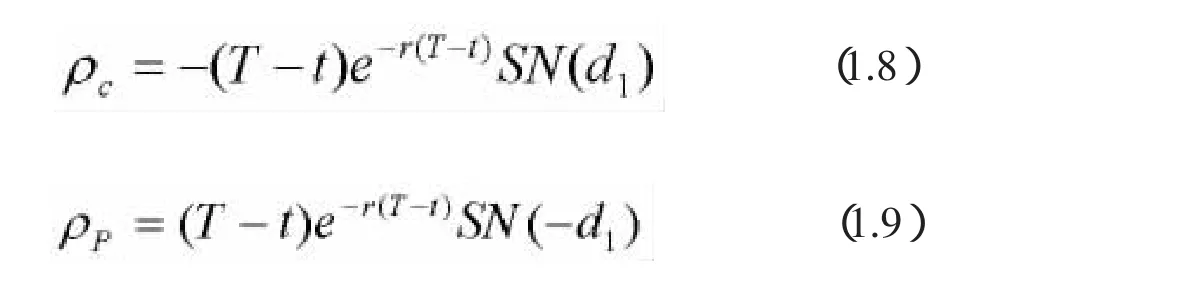
灵敏度分析方法由于简单、直观而在实际中获得广泛应用，针对不同类型的金融资产产生了不同形式的灵敏度。但灵敏度分析方法对产品类型有很高的依赖性，即每一种灵敏度只能测量某一类资产的风险，对于含有大量金融资产的投资组合却显得束手无策，另外，对于测量的各种投资品种的风险也无法做出比较。灵敏度方法只能作为度量以上几种金融市场风险的工具，而对于期货、外汇等一些金融市场还没有找到合适的灵敏度方法。

2 期权定价模型及VaR分析说明

以传统的对冲为例进行分析说明，在此基本资产的价格值St，受到下列随机微分方程的制约：[2]

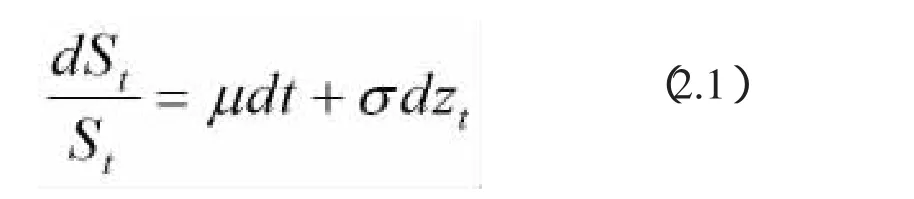
其中μ为漂移资产值，σ为波动性资产值，Zt是一个标准的布朗运动，dZt为一个维纳过程。而且要求证券投资组合回归服从布朗几何运动。采用这个模型分析资产的商品价格、股票或兑换率的风险是比较合适的。

该机构对冲资产的使用看跌期权的价值。定义市场价格时间τ放进Pt=P（St,X,r,τ,σ），期权敲定价格为X，汇率为r。τ为期权有效期内从t开始下一个时间段，我们假设所有期权符合欧式看跌期权，根据Black-Scholes期权定价模型[3－4]，由看跌期权公式有：

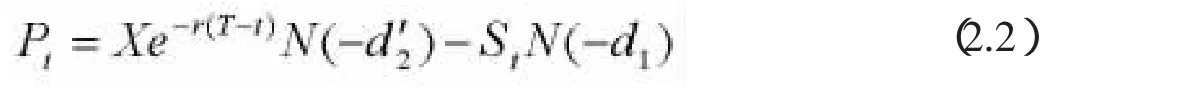
且 Φ（·）是渐增正态分布，看跌期权策略包括买空，hi，i=1，…，n，在 n 期权服从敲定价格 Xi（(i=1，…，n），看跌期权的总数，不能超出适当的下限C。此外，我们假设风险从不充分地对冲，一般而言，这约束条件将不会约束在对冲上合理的费用标准。

VaR的统计定义为：[5]用 (1-α）%的置信度，在τ时期内，在现金流的期货值里的经济损失将不超过VaRt+τ。计算这VaR，首先考虑的非对冲资产的期货值的条件分布是对数正态分布：

C（·）是一个标准的正常累积分布的截止点，VaR式中的第二项仅仅是资产的一个百分比的水平在预期的回报。

期权对冲影响VaR有两种途径：（1）对冲的成本减少世界各国的期货现金流；（2）当他们完成实值期权时，期权的损益增加现金流。随着可行价低于α%标准的期望损益，这不会是最优购买期权的时机，因为他们不接收。因此，对风险值计算的目的，我们可以假定看跌期权在完成认沽期权，所得到的VaR是

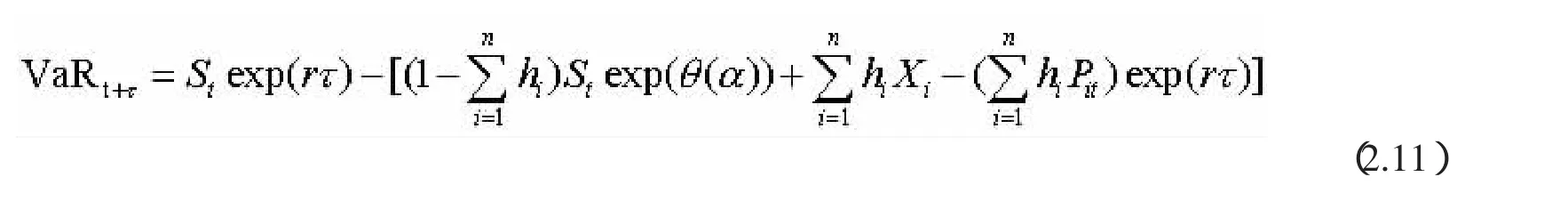
VaR依赖于部分非对冲风险的α%损益、期权的利润以及未来对冲成本的期货值。最后一项的等价解释是投资者借期权的成本支付到期的货款。假设VaR，资产的最优问题是

由上面的等式可得出：首先，VaRt+τ是一个仿射函数的套期保值成本C，它并不影响到选择X的值，X的最优值受资产的现金流所决定，且套期保值比率将调整依赖于对冲成本。结果也证实成本约束是有约束力的事实。在对冲开支中VaR是线性的，所以每个额外支出套期保值交易产生同样的减少货币，没有减少利益套期保值。

其次，方程 （2.14）证明了VaRt+τ的最小值等于在可行价与α%的非对冲损益标准和看跌期权的价格之间的最大比率的距离。不严格地说，约束函数可解释为套期保值及成本效益的套期保值的比率。

方程 （2.14）的最大值问题首要条件是：

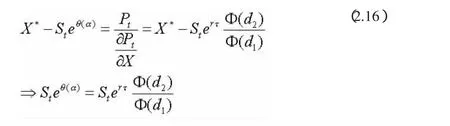
通过以下途径解释主方程 (2.16)，敲定价格的选择以致非对冲头寸的损益的α%等于在可行价期权的中性风险的风险期望。在得到上述解，我们设预先约定C＝hP（X）。因而，h*=C/P(X*)；那就是说，最优可行价格的期套比率是简单的成本与在敲定价格的看跌期权值的比率，尽管X*没有解析解，但X*的解析表达式可根据使用隐函数定理来静态分析。

3 比较静态经济理论分析

又由方程 (2.16)，X满足最优选择

定义 β=(μ，σ，r，τ)，由 X=X(St，β)，利用隐函数定理可得

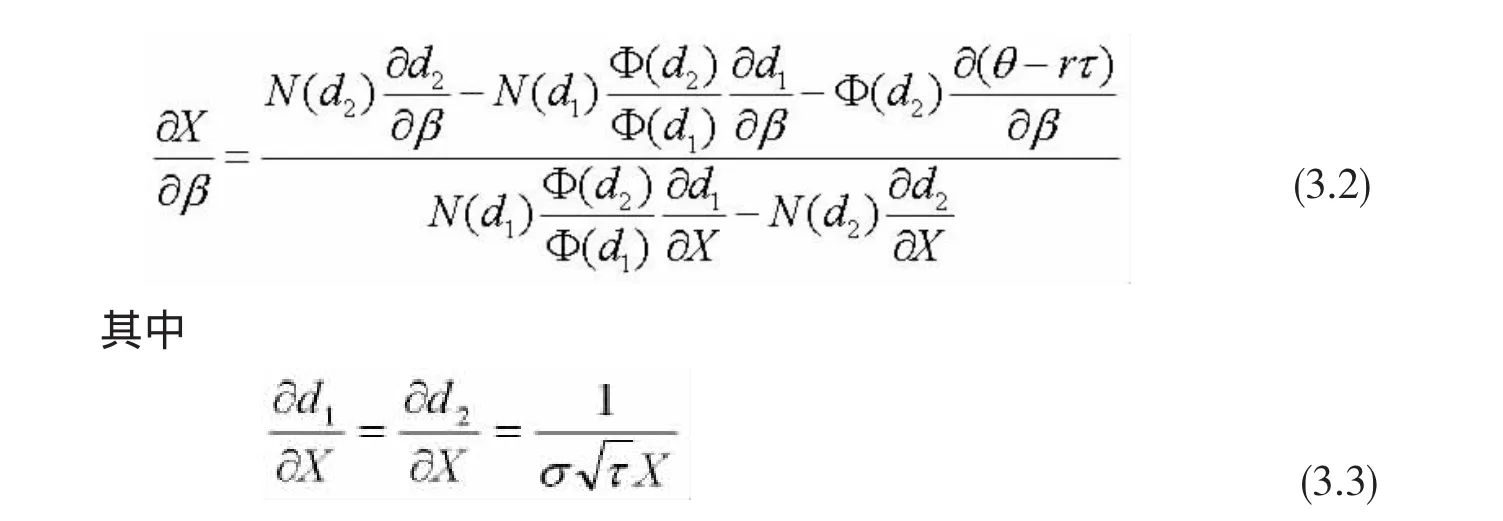
取d1d2的导数服从于参数向量的每个元素β，生成预期比较静态的结果。

最优可行价的导数服从基本资产的漂移

增加分布平均数的作用是与增加最优敲定价格，资产的远期合约分布转向右边与目前值有关。所以，最优可行价增加它的保护关系与非对冲损益的α%标准有关。

最优可行价的导数服从基本标的资产的波动性

这是一个模糊的符号，随着α的增加，看跌期权价格增加，较高的波动性也增加基本标的资产分布的离散性。因而，可行价必须降低它的保护关系与非对冲损益的α%标准。既然作用在相同的方向上，我们可以期望随α的上升，最优敲定价格下降，对于许多参变量来说是正确的。然而，如果α＞50%，那么非对冲分布α%值在波动性中增加，非对冲VaRt+τ值在波动性中减少。因一个足够高的α的作用能抵消成本的作用，且最优可行价在波动性中增加。

最优可行价的导数服从无风险率

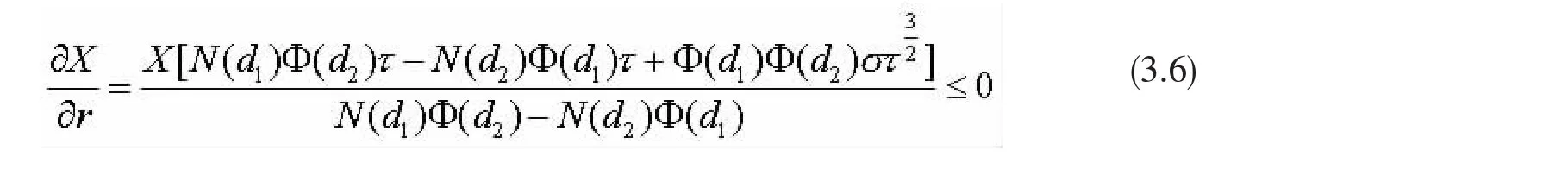
随着利率的增加，最优敲定价格减少，最优敲定价格下跌是因为看跌期权的成本一致下跌。当然，因为作用在成本上是小的而且没有作用在基本标的资产的分布上，大致利率作用的改变是小的。

最优可行价的导数服从套期范围

偏微分的期权对冲发生的范围是很大的，然而是非单调的，作用在货币期权的最优标准上。一方面，随着增加范围，资产回归支配正漂移与执行价格上升反映该资产的价值的分配偏离其当前值。另一方面，资产波动性增大它的范围，且分布变得更加分散，导致更低的最优可行价。随着范围变长，在前面的结果占优势，敲定价格增加。对较短的范围而言，波动性效果占优势，可行价减少。一般地说，这个逆转总会发生的 （只要漂移是正的）；然而，它的转折点依赖于基本参数值本身。

最后要考虑的问题是如何使最优敲定价的改变作为一个投资合理保护标准的函数，那就是说，分布函数的百分尾部用来计算VaR。再次，用隐函数定理，

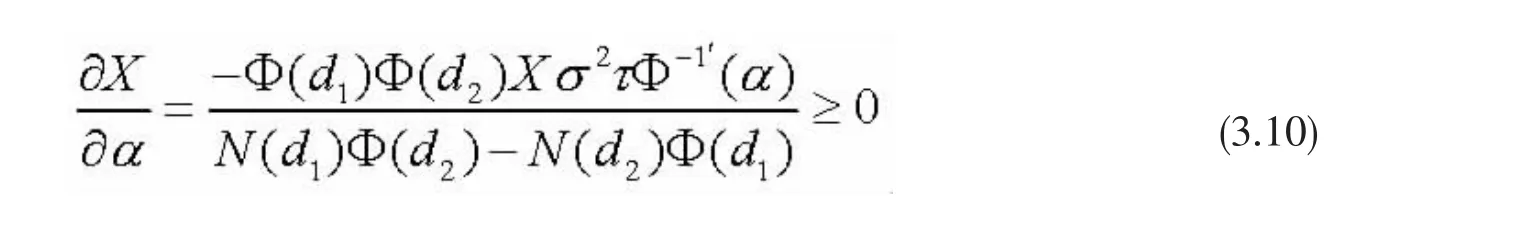
其中Φ－1′（·）是渐增正态分布函数Φ （·）的导数的反函数，分子与分母都是负的，所以最优可行价在α中是增加的，这结果与前面的结论相吻合。

4 结论

本文就期权定价模型,从期权定价公式进行探讨，对期权风险管理的各个因素在VaR约束下进行静态经济分析，从而探讨期权风险管理的最优的解。对于投资者对期权风险管理提供非常重要的参考价值。

[1]John C.Hull.期权、期货和其他衍生产品[M].张陶伟，译.北京：华夏出版社，1999：2-6,280-297.

[2]Ruey S.Tsay.金融时间序列分析[M].潘家柱，译.北京：机械工业出版社,2005：180-186.

[3]罗伯特·豪根.现代投资理论[M].郑振龙，译.北京：北京大学出版社，2005：421-495.

[4]王春峰.金融市场风险管理[M].天津：天津大学出版社，2001：69-194.

[5]Giorgio Szego.Measure of risk[J].Journal of Banking ＆ Finance,2002,26(8)：1253-1272.

[6]Peter Christoffersen,Jinyong Hahn,Atsushi Inous.Testing and comparing Value-at-Risk measures[J].Journal of Empirical,2001,8(3)：325-342.

A Static Research into the Optim ized Solution to Option Risk M anagement under M odel VaR

Luo Wenhui1,Li Lianfen2
(1.Education and Education Technology Department of Jiangmen Polytechnic,Jiangmen 529090,China;2.M athimatics and Physics Department ofWuzhou University,Wuzhou 543002,China)

The Model VaR for option riskmanagement is amethod tomeasure the option risks in financialmarkets.This paper makes a static research into themanagementof option risks under Model VaR,an option pricingmodel,so thatan optimized solution to option riskmanagement is obtained.

VaR；option；optimized solution；static research

F830.9

A

1673-8535(2010)03-0036-08

骆文辉 (1971－)，男，广东人，江门职业技术学院教育与教育技术系数学讲师，硕士研究生，主要研究方向：金融数学。

李连芬 （1977-），女，广西贵港人，梧州学院数理系讲师，主要研究方向：概率统计与金融数学、数学教学论。

（责任编辑：覃华巧）

2010-03-01