让探究学习与课堂教学零距离

●张 俊 (兴化市第一中学 江苏兴化 225700)

新课标倡导数学课程应通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程.在课堂上开展数学探究活动，从而培养学生的探索意识、创新能力，已成为一个亟待解决的热门问题.笔者认为，精心挑选一个有发展潜质的问题，把教学过程设计成一个探索发现的过程，充分展示数学的内在魅力，在教师的引导下以学生为主体展开探究活动是落实这一新课标理念的一种有效方法.本文以一道几何题为例介绍笔者在这一课题研究中的一次尝试和体会.

1 探索历程回放

题目如图1，已知DO平分∠ADC，BO平分∠ABC，且∠A=27°，∠O=33°，求∠C 的大小.

此题是单元测试卷中的一道试题，看似平淡无奇，实则内涵丰富，学生给出的解答方法也是绚烂多姿、异彩纷呈.在让学生展示了他们各自优美的解法后，笔者引导学生回顾解题过程，去除非本质因素，提炼出一般化结果.

探究1 在图1中，易知

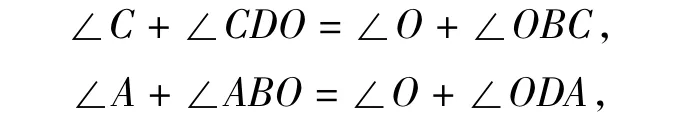
两式相加并利用∠CDO=∠ODA，∠ABO=∠OBC，可得

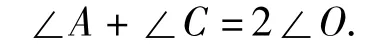
由此可得命题1.

命题1 如图1，若∠D，∠B的角平分线交于点O，则∠A+∠C=2∠O.

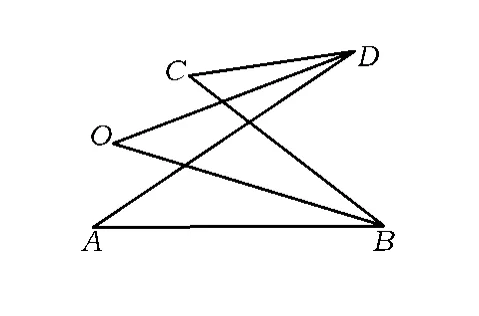
图1

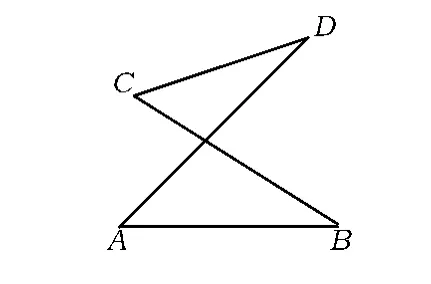
图2

会做一道题，仅仅是给别人作了一次奴隶，怎样从奴隶到将军呢?就是以一道题为源头，经过创造性思考获得与此相关的一系列问题，并能向纵深发展，得到更深层次的东西.基于以上认识，获得命题1后，进一步引导学生作了如下探究.

探究2 如图2，作∠D，∠B的角平分线得到图1，进而探得命题1.那么在图2中作∠D，∠B外角平分线，又将获得什么呢?

学生或动手、或沉思、或讨论，很快就有人得到了结果.为了便于更进一步的诱“题”深入，笔者提示学生将此问题化归为命题1来解决.

如图3，设点P是∠D，∠B外角平分线的交点.由邻补角的角平分线互相垂直，得

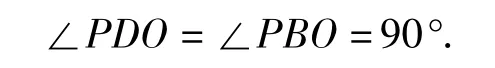
利用四边形内角和为360°及命题1得

由此可得命题2.

命题2 如图3，若∠D，∠B的外角平分线交于点P，则

探究3 在图2中作∠D，∠B的外角平分线，又将获得什么呢?

类似命题2的方法，不难得到命题3.

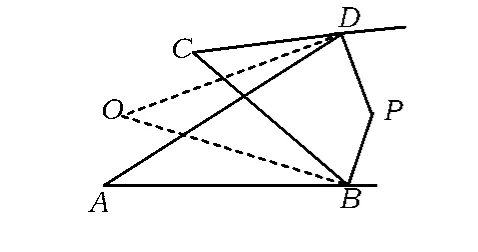
图3

图4

命题3 如图4，若∠D，∠B的外角平分线交于点Q，则

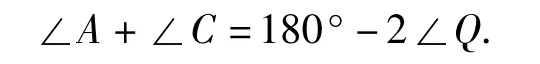
化归思想不但是数学家最强大的武器，也是每一个中学生应该领悟并掌握的一种重要的数学思想方法.从上述问题的探究过程中，学生亲身体验到了这一思想方法的巨大火力，不用千言万语，化归思想自然会成为学生今后解决问题的一种有效的工具.

探究4 如果在图2中作∠D，∠B的三等分线，那么又将出现怎样一番景象呢?

如图5，点 O1，O2是∠D，∠B三等分线的交点，易知

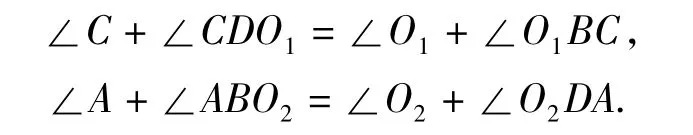
以上两式相加并利用

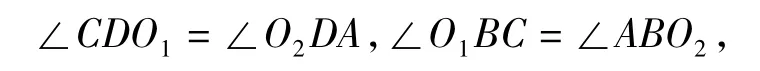
化简可得

由此可得命题4.

命题4 如图5，若∠D，∠B的三等分线交于点 O1，O2，则∠A+∠C=∠O1+∠O2.

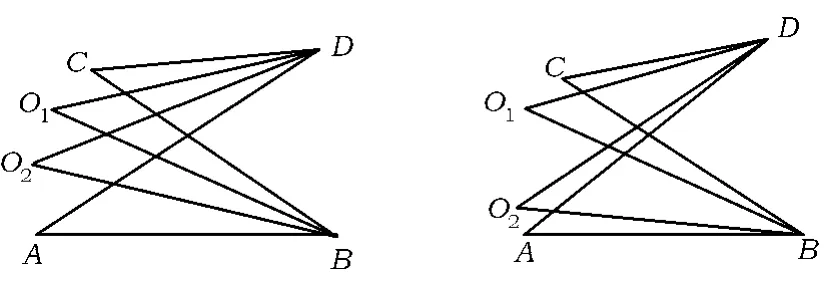
图5

事实上，可进一步获得命题5.

命题5 如图 6，若 ∠CDO1=∠O2DA，∠O1BC=∠ABO2，则∠A+∠C=∠O1+∠O2.

探究5 在图2中作∠D，∠B外角的三等分线，设其中2个交点为P1，P2(如图7)，易知

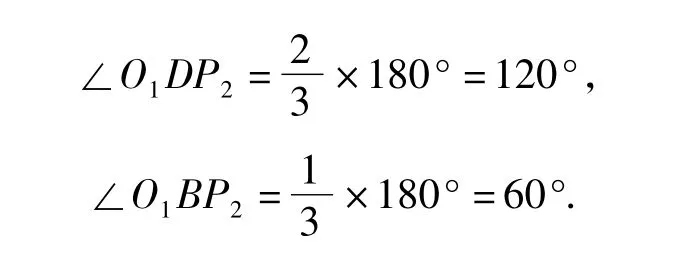
从而由四边形内角和为360°，得∠O1与∠P2互补.同理可得∠O2与∠P1互补，故

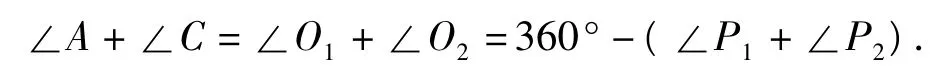
由此可得命题6.

命题6 如图7，若∠D，∠B外角的三等分线交于点 P1，P2，则∠A+∠C=360°-(P1+P2).

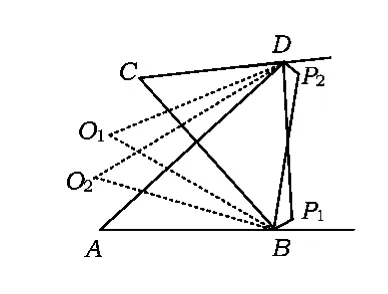
图7

图8

类似命题6的探究过程可得命题7.

命题7 如图8，若∠D的三等分线与∠B外角的三等分线交于点Q1，Q2，则

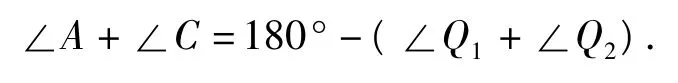
由一个命题得出了一个新命题，一个新命题解决了，又一个新命题诞生了…….学生体验着探索的乐趣，享受着发现的成功.这种探索式的课堂教学设计，远比孤立地解现有题目更能营造探索、思考、交流与发现的创新空间，焕发他们主动学习和创新的欲望.

经过以上的教学过程，笔者觉得此时放手让学生独自探索的时机已经成熟，于是建议学生或分组合作、或自我探索，已期获得更多的成果.

学生思维的火花一旦点燃，想象力和创造力真是无穷无限.很快，学生就纷纷拿出了自己的成果.经笔者整理补充，摘录如下.

2 学生部分成果展示

命题8 如图9，AD，BC相交于点M，∠A，∠C的角平分线交于点O2，∠B，∠D的角平分线交于点 O1，则∠O1+∠O2=∠DMB.

图9

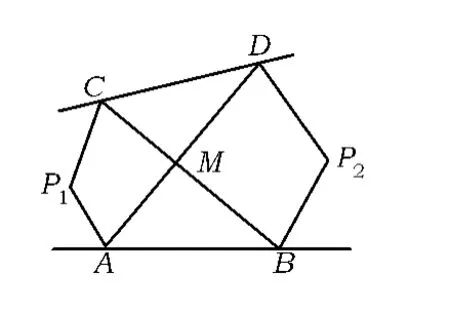
图10

命题9 如图10，AD，BC相交于点 M，∠A，∠C的外角平分线交于点P1，∠B，∠D的外角平分线交于点P2，则

命题10 如图11，AD，BC相交于点 M，∠A，∠C的角平分线交于点Q1，∠B，∠D的角平分线交于点 Q2，则

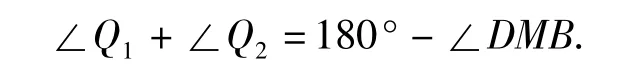
命题11 如图12，AD，BC相交于点 M，∠A，∠C的三等分线交于点O3，O4，∠B，∠D的三等分线交于点 O1，O2，则

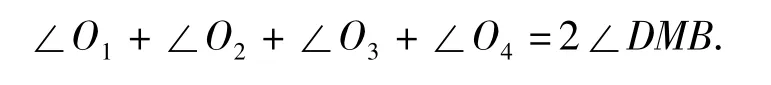
图11

图12

命题12 如图13，AD，BC相交于点 M，∠A，∠C的角平分线交于点O3，∠B，∠D的三等分线交于点 O1，O2，则

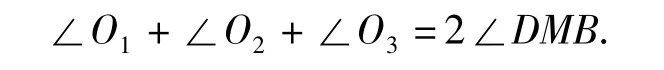
命题13 如图14，∠B，∠D的三等分线交于点 O1，O2，∠B，∠D 的外角平分线交于点 P，则

∠O1+∠O2=360°-2∠P.

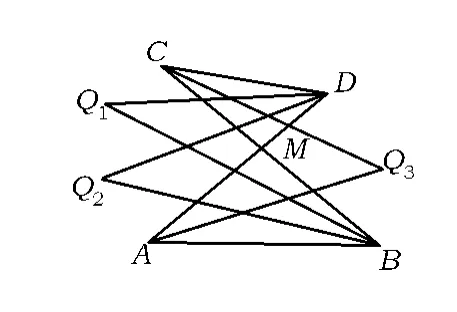
图13

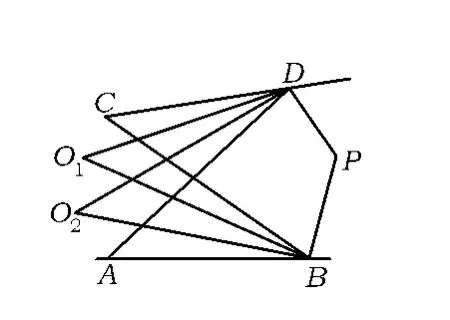
图14

波利亚说过：“一个专心的、认真备课的教师，能够拿一个有意义、但又不复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入到一个完整的理论领域.”通过本案例可以发现，在教学中，教师如果能科学、合理地运用这种“有意义，但又不复杂”的问题展开教学，充分发挥其潜在的教育功能，那么对减轻学生负担，开发智力，提升思维品质，逐步培养探究气质和研究能力都是大有裨益的.