构造一次函数解证不等式问题

●华腾飞 (黄湾中学 安徽灵璧 234213)

构造一次函数解证不等式是一种强有力的工具.下面举例说明之，希望对大家能够有所启迪.

1 求参数范围

例1 已知函数y=(x-1)log23a-6log3ax+x+1，其中当 x∈［0，1］时，函数恒为正，求 a的取值范围.

分析选x为主元，构造一次函数

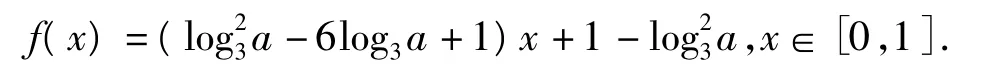
一次函数恒为正的充要条件为

分析依题意得a=b=1-c，于是

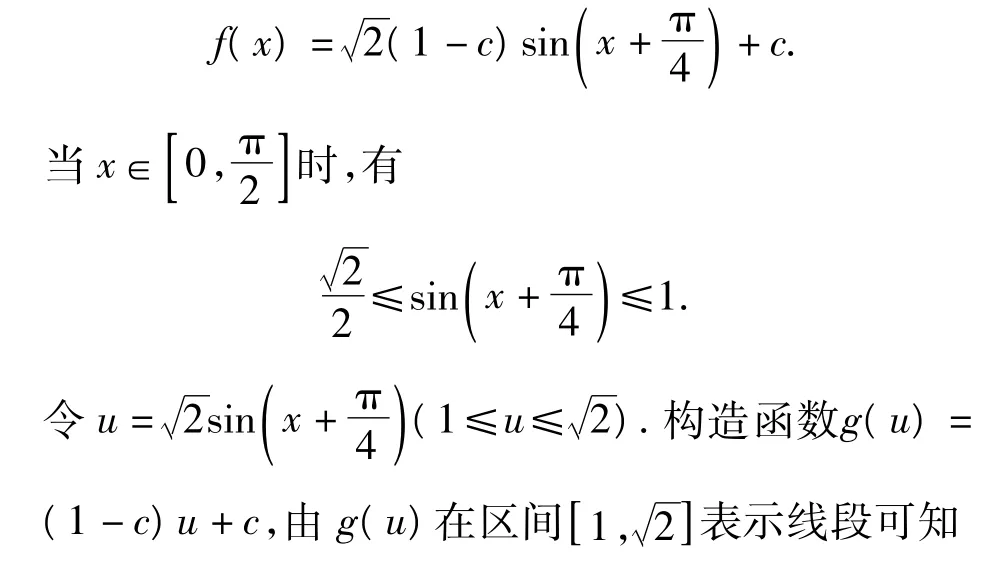
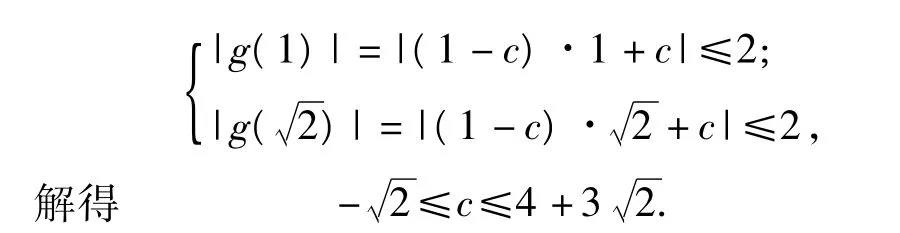
评注上述2个例子若不变换主元，则需进行分类讨论，运算过程非常冗长，不利于构造参数不等式求范围.

2 解不等式

例3 设不等式x2+px+1＞3x+p对一切满足|log2p|＜2的值均成立，解此不等式.

分析转换视角，将不等式中的p视为主元，则原不等式可变形为

问题转化为关于p的一次函数为正数时系数的讨论.显然x≠1，因此 f(p)是 p的单调函数，使得f(p) ＞0( p ∈ (1

，4 ) )成立的充要条件为4

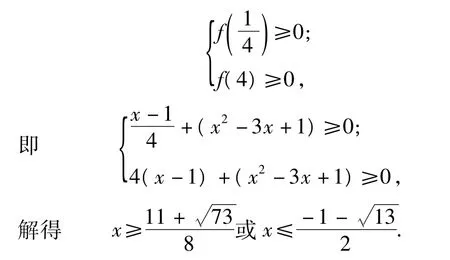
3 证明不等式

例4 设d为正数a，b，c，d中的最大数，求证：

证明构造一次函数

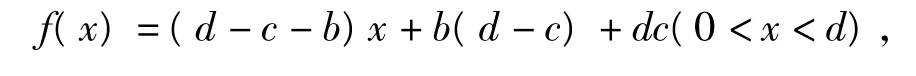
从而无论一次函数f(x)是增函数还是减函数，当x∈(-1，1)时，恒有 f(0) ＞0，即

于是问题获证.

证明原不等式等价于

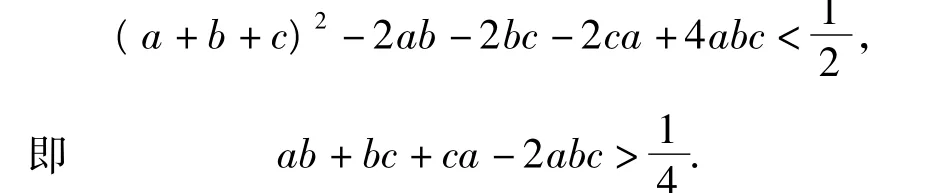
由三角形两边之和大于第三边及a+b+c=1，可知

构造一次函数

例9 已知 a，b，c是△ABC的3条边长，若△ABC的周长为2，求证：a2+b2+c2+2abc＜2.

证明由已知条件a+b+c=2易知，原不等式等价于

又由三角形两边之和大于第三边及a+b+c=2，

可知

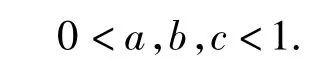
为此可构造一次函数

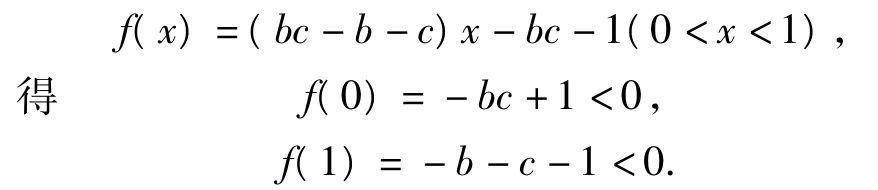
于是对0＜x＜1，都有f(x)＜0，即

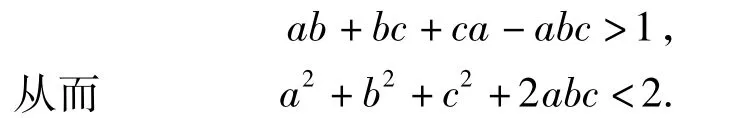
例10 试证：如果对于所有的x∈［-1，1］，不等式|ax2+bx+c|≤1成立，那么对这些x的值，不等式|cx2-bx+a|≤2也成立.

证明由绝对值不等式，得

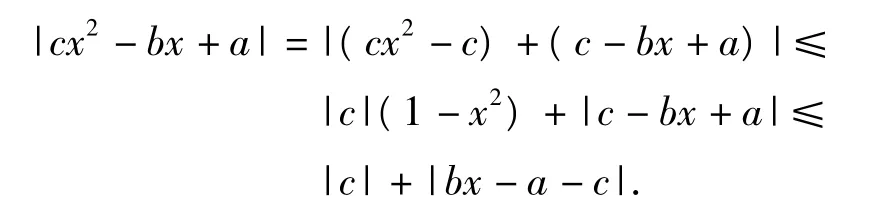
令g(x)=-bx+a+c，则只需证明g(x)≤1，对于x∈［-1，1］成立.由 g(x)在［-1，1］上的图像可知

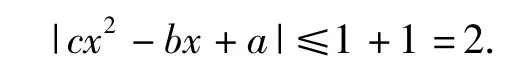
又由已知当x=0时，|c|≤1，得例11 已知a，b，c是实数，函数

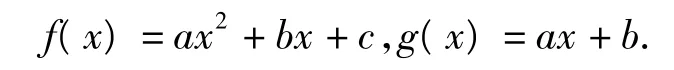
当 -1≤x≤1 时，|f(x)|≤1，求证：当 x∈［-1，1］时，|g(x)|≤2成立.

所以对于函数 g(x)=ax+b，x∈［-1，1］，有

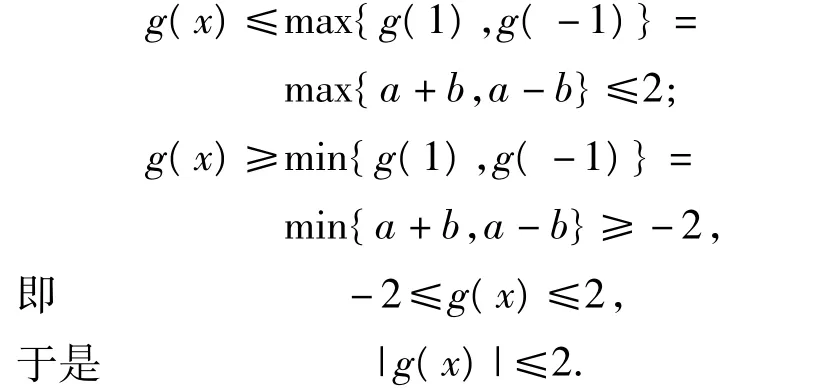
例12 正数 a，b，c，A，B，C 满足条件 a+A=b+B=c+C=k，证明：aB+bC+cA ＜ k2.

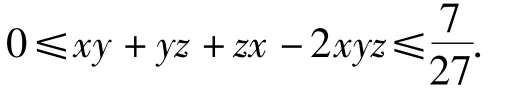
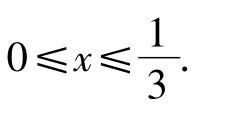
(1)先证左边的不等式，可构造一次函数

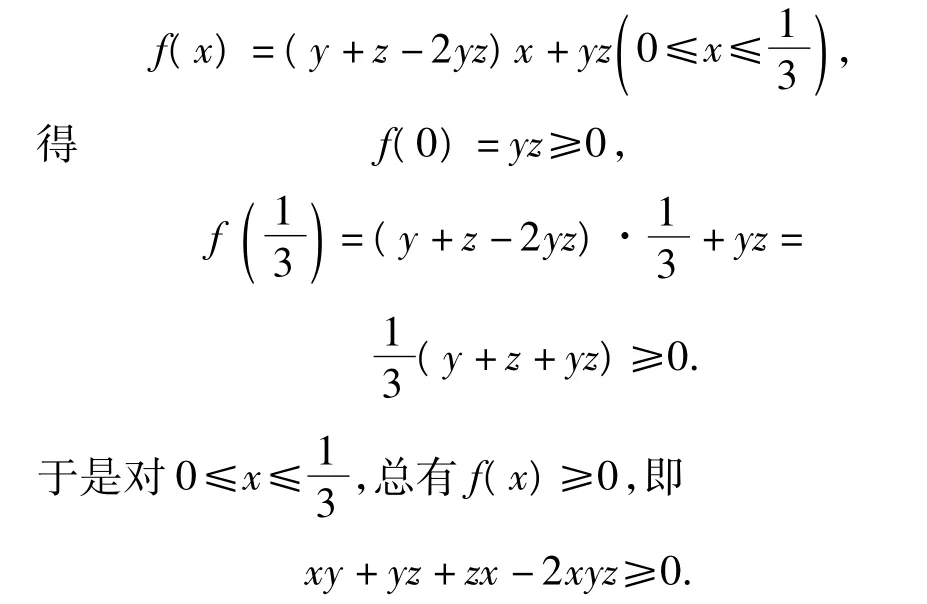
(2)再证右边的不等式，可构造一次函数

由以上数例可以看出一个共同特点：对于难度较大的不等式问题，通过将已知条件经过适当的逻辑组合构造出一次函数，利用一次函数的性质可使问题简捷获解.当然，前提条件是必须进行巧妙地变形，同时还需要灵活地构造一次函数，利用其在有界区间上的函数值的有界性进行判断和证明.因为函数与方程、不等式关系非常密切，巧妙构造辅助函数解题在不等式中具有独特的作用.