三圆幅值法找动平衡原理

余秋兰 张 键

作者通联：武汉工程职业技术学院汽车工程系 武汉市 430080

E-mail：fishever@163.com

三圆幅值法是现场找动平衡的方法之一，与影响系数法相比，三圆法的优势在于不需要精确地测量不平衡矢量的相位角，对测量仪表的配置要求低。不测相位角，只测最大振动幅值，适合很多缺乏精密仪器需要找动平衡的场合。但三圆幅值法只适用于刚性转子的单面动平衡，即单盘、中低速转子。这类转子工业现场应用最多，几乎占所有工业转子的90%，所以三圆幅值法仍有广泛的应用范围。

在一些论及现场动平衡技术的书籍中，只有三圆幅值法现场操作步骤的讲述，缺乏对这个方法的理论证明。从而导致一些专门讲述现场动平衡技术的书（如国防工业出版社出版的《转子现场动平衡技术》2007年版）避而不讲三圆幅值法，只讲影响系数法。本文的目的是简述三圆幅值法的运用原理。

一、三圆幅值法现场动平衡操作步骤

（1）将待平衡的刚性转子配重槽圆周三等分，等分点用A、B和C表示，圆心用O表示，夹角都为120°（图1）。

（2）加试重，取试重p单位克（g）。

（3）将试重分别放在 A、B、C三点上，三次开机运转测得振幅分别为：A点振幅Ra；B点振幅Rb；C点振幅Rc单位均为微米（μm）。

（4）用相同的比例，作振动向量图：以初始机器运转时的振幅Ro为半径画圆。在Ro圆上等分三点，夹角为120°，编号也用A、B、C表示，参照图1；以A为圆心，以Ra为半径画圆；以B为圆心，以Rb为半径画圆；以C为圆心，以Rc为半径画圆；在图2中，圆Ra和圆Rb交于a点，圆Ra和圆Rc交于b点，圆Ra与圆Rc交于c点；连接abc三点，并作△abc的外接圆，圆心为O1，如图3所示；连接圆心O、O1；测量OB和O、O1的夹角，用α来表示。

（5）平衡质量的计算和平衡位置的确定。平衡质量m=pR0/OO1，单位（g）。平衡位置在刚性转子上，从B点向A点移动角度α。

图1

二、三圆幅值法的运用原理

三圆幅值法是现场寻找转子动平衡的一种经验法，书本上很少有介绍，在此简单证明其可行性。

若转子在未加任何试重的情况下，测得的原始不平衡矢量的振矢大小为Ro，该矢量方向未知。由于该矢量的方向未知，分别讨论若该矢量位于以下三种情况下的三圆幅值法的运用原理。①若原始不平衡矢量R0的方向与图1中OA、OB、OC某一方向重合。②若原始不平衡矢量R0的方向与图1中线段AB、AC、BC的三条垂直平分线中某一条平分线重合。③一般情况。原始不平衡矢量除以上两种情况以外的方向。由于一般情况更具普遍性，因此主要证明一般情况。

1.一般情况

（1）在A点添加试重。理想状态下，若转子处于理想平衡状态时，在A点添加质量为为W（g）的试重，若此试重产生的振矢为Rw，则此方向必沿OA方向。但Rw大小无法测量。

图2

图3

实际状态下，若原始不平衡矢量的R0方向如图4中OC所示，A点添加质量为W（g）试重后，可测得转子此时的合成不平衡量振矢，大小为Ra，矢量方向无法测量。但矢量Rw、Ro、Ra必满足图4中平行四边形OABC，其中矢量图中OB，OC的长度已知，OA的方向已知。

（2）在B点添加试重。去掉A点所加试重W，在图1中圆盘B点添加同样的试重，则三个振矢Ro，Rw，Rb同样有如图5所示平行四边形其中 OD、OC的长度已知，DE的方向已知，如图5所示与OA的夹角为120°。

图4

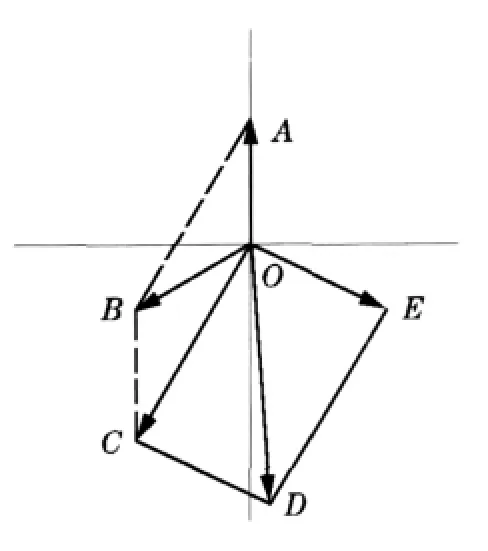
图5

由于试重W所产生的矢量长度为OA（该长度未知），原始不平衡质量m（方向未知）所产生的矢量长度为OC（已知），故要求解试重W产生的振矢大小也就转化成了求OA的长度。

（3）利用几何作图法确定线段OA的长度

将所有矢量转化到矢量三角形中，如图6所示，图中∠AOE=120

将矢量三角形ODE逆时针旋转120°，则有图7，图中OA=Rw，BE=ED=Ro，OD=Rb，OB=Ra。则图 7 中为原始不平衡量长度等于原始不平衡量振矢大小，图7中矢量三角形BAO与三角形DAO有了公共矢量此变换是为了便于几何求解。

作图。以O为圆心以Ro为半径画圆，将圆3等分，∠AOB=∠BOC=∠COA=120°，由图7可知分别在转子A点、B点添加试重后两个试重产生的不平衡矢量角度为120°。故可令图8中的等同于图7中的矢量图8中的等同于图7中的矢量

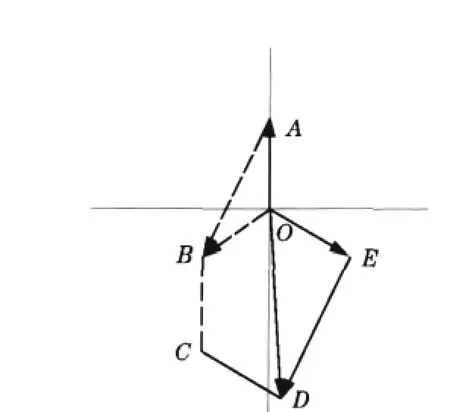
图6

图7

以A点为圆心，以Ra为半径画圆，则圆A的圆周上必存在一点M，使得三角形OAM全等于图7中的三角形EBO。其中合成振矢 Ra，而且使

再以B点为圆心，以Rb为半径画圆，则圆B的圆周上同样必有一点N，使得三角形OBN全等于图7中的三角形EDO。由图7可知是两个三角形的公共边，具有唯一性，故在图8、9中一样具有唯一性，即矢量，即M、N是同一个点，也就是说该点即在圆A上也在圆B上，即该点为圆A与圆B的交点。由于两圆的交点一般为两个，但是试重的矢量长度肯定只有一个数值，要确定哪一个，就需要补画圆C（以C为圆心，以Rc为半径画圆）。同理可得该点也必在圆C上。故从理论上讲，A、B、C三圆必有一个共同的交点，该交点满足所有的全等三角形限定条件。但是因为存在测量误差、作图误差，导致这三个圆不能交于一点，这样就构成了误差三角形△abc。误差三角形△abc是三圆交点所构成的所有三角形中面积最小的那个三角形。

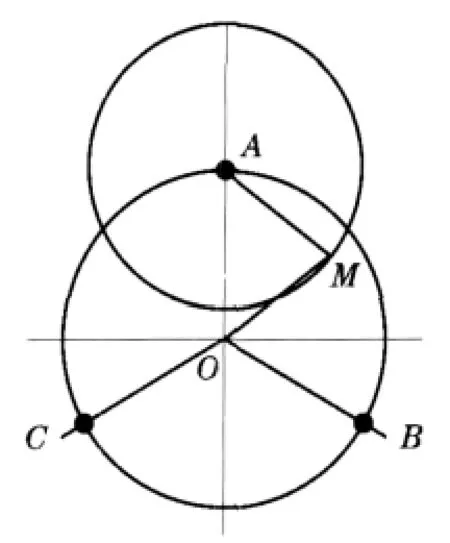
图8

图9

2.特殊情况一

原始不平衡矢量与某个试重加载位（A、B、C中任一点，假定为C点）重合。在这种情况下，试点C因为试重与原始不平衡质量同在一条线上，振矢大于Ro，因此所画圆弧越过O点，画在OC线段的反方向上；因A、B点的位置对称于OC线，且在反方向，所以试重加在这两点的合成振矢小而且相同，即A圆、B圆形成对称的状态。如图10所示。三圆相交于K点，OK线段即为试重所产生的振矢，OC为原始不平衡质量所产生的振矢Ro。平衡质量m=W×OC/OK，单位克（g），平衡位置在OK的延长线上，A点、B点中间，C点的相对位置。

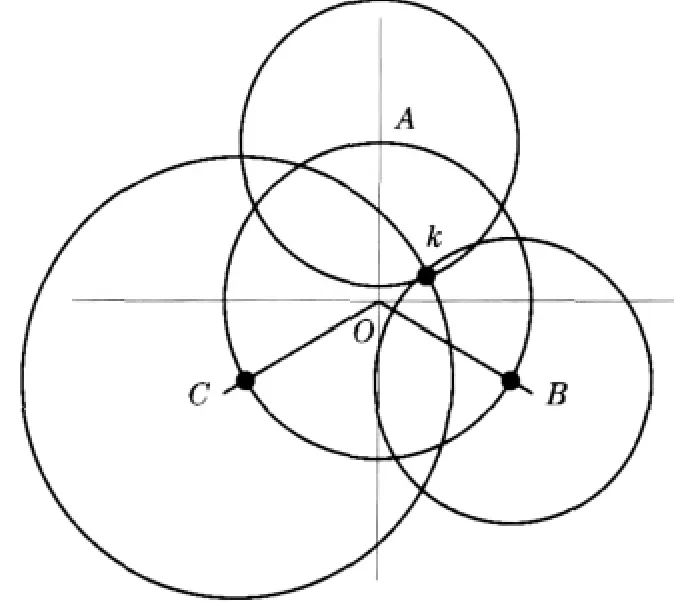
图10

3.特殊情况二

原始不平衡矢量恰好位于两个试重加载位（A、B、C中任一点）的中间，即原始不平衡矢量Ro的方向与图 1中线段 AB、AC、BC的三条垂直平分线中某一条平分线重合。假定该矢量位于B、C中间。在这种情况下，C圆与B圆大小相等且对称于OA线。因为A点恰在原始不平衡质量的相反位置，因此振矢最小，所绘图形如图11所示。三圆相交于K点，OK线段即为试重W所产生的振矢，OC为原始不平衡质量所产生的振矢Ro。平衡质量m=W×OC/OK，平衡位置在OA的延长线上。

图11

三、小结

由于三圆幅值法在现场找动平衡时，受到测量误差、作图误差的影响，特别是手工作图误差难以减小，所以现场动平衡的精度低于其他使用高精度仪器的动平衡方法。但是在大多数情况上平衡精度足够，平衡误差可以降到许可范围内。