以位移为基础的连续梁桥抗震设计

魏 标,李 欣,李建中

(1.中南大学 土木建筑学院,长沙 410075;2.同济大学a.建筑设计研究院(集团)有限公司市政工程分院;b.桥梁工程系,上海200092)

最近十几年,基于位移的抗震设计方法得到了迅速发展,并被美国AASHTO规范(2007)[1]等采用。在基于位移的抗震设计方法中,地震作用下结构弹塑性位移需求预计是首先遇到的问题,虽然可以采用非线性时程分析方法计算结构在地震作用下的弹塑性位移需求,但计算分析复杂,因此各国学者致力于发展地震作用下位移需求预计的简化方法[2-8]。其中,利用地震作用下结构弹性位移需求,并考虑位移修正系数,来代表结构的弹塑性位移需求是其中的一个发展方向。Riddell(1989)[9]和Miranda(2000)[10]等针对单自由度结构体系,对位移修正系数进行了研究,并给出了具体表达式,尽管形式各不相同,但都有一个共同的特点:对周期相对较长的结构,各种简化方法对应的位移修正系数都近似等于1,即等位移准则。部分规范[11]在对桥梁进行抗震设计时,采用了等位移准则;郭磊[11]对等位移准则在连续梁桥纵桥向的抗震设计中的应用也进行了研究。

然而,上述研究均是针对单自由度体系或等效单自由度体系进行。对于连续梁桥,尤其非规则连续梁桥,高阶振型影响显著,在此情况下,如何利用地震作用下的结构弹性位移来预计连续梁桥的弹塑性位移是各国学者所关注的问题。

该文采用非线性时程分析方法和弹性反应谱分析方法,分别计算了典型连续梁桥的横桥向的位移需求,并对2种方法得到的位移需求进行了参数分析和对比分析,在此基础上,采用统计分析方法得出了一种连续梁桥横桥向的位移需求预计的简化方法,并应用于连续梁桥横桥向的基于位移的简化抗震设计。

1 单自由度体系

针对地震作用下的单自由度体系结构的位移反应特点,Clough等[12]建立了单自由度体系结构的弹性位移需求 Δe与弹塑性位移需求 Δu之间的关系,即

其中,T为单自由度体系结构的周期,μ为位移延性需求系数,为最大地面位移。

由式(1)看出,对于周期较长的单自由度体系结构,弹性位移需求与弹塑性位移需求近似相等,即满足等位移准则。

近些年来,许多学者对此有了进一步的发展,大量的理论[9-10]表明,地震作用下单自由度体系结构的弹塑性位移需求可根据其相应的弹性位移需求修正得到,即:

其中,C为位移修正系数。

由式(2)看出,通过弹性位移需求来得到弹塑性位移需求的关键是位移修正系数C的确定。许多学者对C的取值进行了大量分析,其中Miranda提出的位移修正系数C的计算公式[10]如下

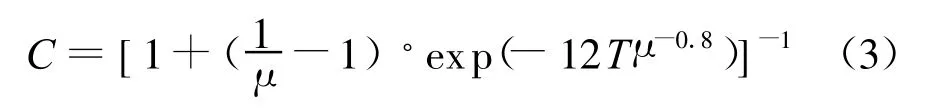
由式(3)看出,C的取值主要与结构的周期T和位移延性需求系数μ有关,对μ取不同的值(分别取为 1.5 、3.0 、6.0、9.0),利用式(3),得到位移修正系数C随结构周期T和位移延性需求系数μ的变化,如图1所示。

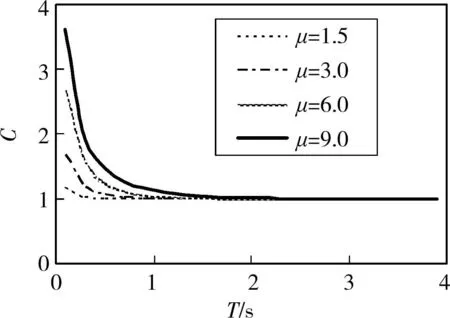
图1 位移修正系数C随结构周期T和位移延性需求系数μ的变化

根据图1,随着结构周期T的增加,不论位移延性需求系数μ取值如何,位移修正系数C趋向于1,即弹性位移需求等于弹塑性位移需求,此时等位移准则成立;如定义位移修正系数C接近1时相应的结构周期T为等位移准则临界周期Tl,则由图1看出,位移延性需求系数μ越大,相应的等位移准则临界周期T l越长。

假设弹塑性位移需求与弹性位移需求的相对差值允许在±5%范围以内,令C=1.05,利用式(3),得到结构的周期T和位移延性需求系数μ的关系如图2所示,曲线拟合得到单自由度体系等位移准则临界周期T l的表达式如下式所示:

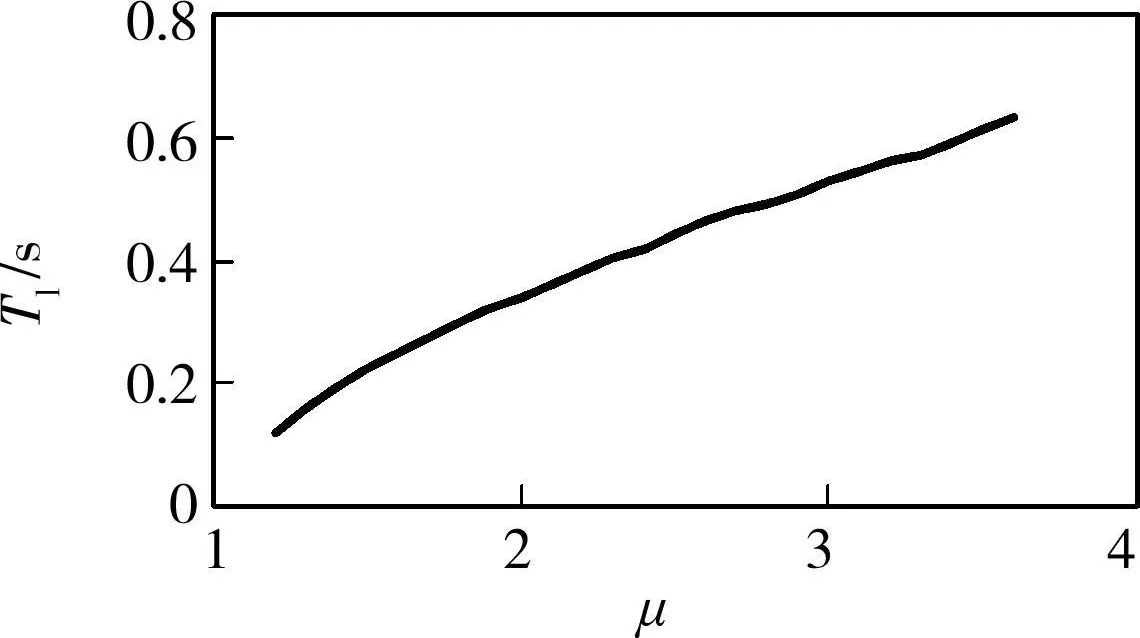
图2 单自由度体系等位移准则的临界周期

2 连续梁桥横桥向位移需求简化计算方法

根据结构在地震作用下的动力响应的复杂程度,连续梁桥可以分为规则梁桥和非规则梁桥。对于规则梁桥,可以近似等效为单自由度体系来简化计算,若主要振型周期大于或等于式(4)中的临界周期T l,则符合等位移准则。对于非规则梁桥,可以采用Chopra的多模态推倒分析方法[13-14],先分别计算各主要振型对应的位移需求,最后再组合得到结构总的位移需求;若结构的所有主要振型对应的周期都大于或等于式(4)中的临界周期T l,则此结构理论上符合等位移准则。

下面采用参数分析方法来具体探讨地震作用下连续梁桥横桥向的弹性位移需求和弹塑性位移需求的关系。应用美国加州大学编制的Opensees程序分别进行非线性时程分析和弹性反应谱分析。弹性反应谱分析时,桥墩采用弹性梁单元模拟,桥墩截面抗弯刚度取为有效刚度[11];非线性时程分析时,桥墩采用非弹性梁单元模拟,结果取为7条时程波计算结果的平均值(7条时程波对应同一弹性反应谱)。

2.1 桥梁结构几何参数

连续梁桥形式多样,此处以4跨连续直桥为背景(见图3),变化墩高得到3座典型连续梁桥,对应的结构几何特性如表1所示。在进行研究时基本假设如下:

1)桥台与主梁的连接:横桥向水平放松;

2)墩底固结。

图3 典型的连续梁桥

表1 3座典型连续梁桥的结构几何特性

为了进行参数分析,在进行弹性反应谱分析和非线性时程分析时,以表1中的3座桥梁为基准,对主梁截面、桥墩截面、跨径分布以及墩高分布等参数进行了变化,具体参数变化如下:

1)改变主梁截面特性:抗弯惯性矩变为参考值的0.5、1.0、2.0、4.0倍,其它因素不变;扭矩变为参考值的 0.5、1.0、2.0、4.0倍,其它因素不变;面积变为参考值的0.5、1.0、2.0、4.0倍,其它因素不变。

2)改变桥墩截面特性:桥墩截面分别取为1.0m×1.0m、1.5m ×1.5m 、2.0m ×2.0m 和2.5m×2.5m,其它因素不变;桥墩截面配筋率分别取为0.4%、0.8%、1.2%和1.6%,其它因素不变。

3)改变跨径分布:单跨跨径变为参考值的0.5、1.0、1.5、2.0倍,其它因素不变。

4)改变墩高分布:2#墩取为5m,1#和3#墩分别取为5m、10m、15m和20m,其它因素不变;2#墩取为10m,1#和3#墩分别取为 5m、10m、15m和20m,其它因素不变;2#墩取为15m,1#和3#墩分别取为5m、10m、15m和20m,其它因素不变。

2.2 地震动输入

弹性反应谱分析采用中国公路工程抗震设计规范(JTJ 004-89)中的I、II、III和 Iv类场地反应谱(见图4);对于每类场地反应谱,采用Simqke程序[15]生成7条加速度时程波作为相应的非线性时程分析的地震动输入,其中,某条加速度时程波见图5,其它加速度时程波与此类似。

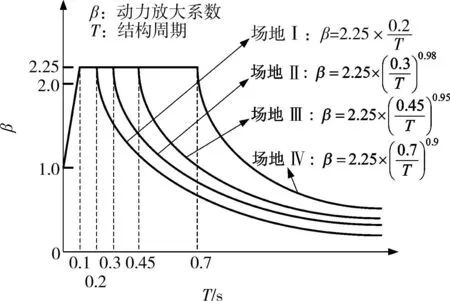
图4 4类场地反应谱

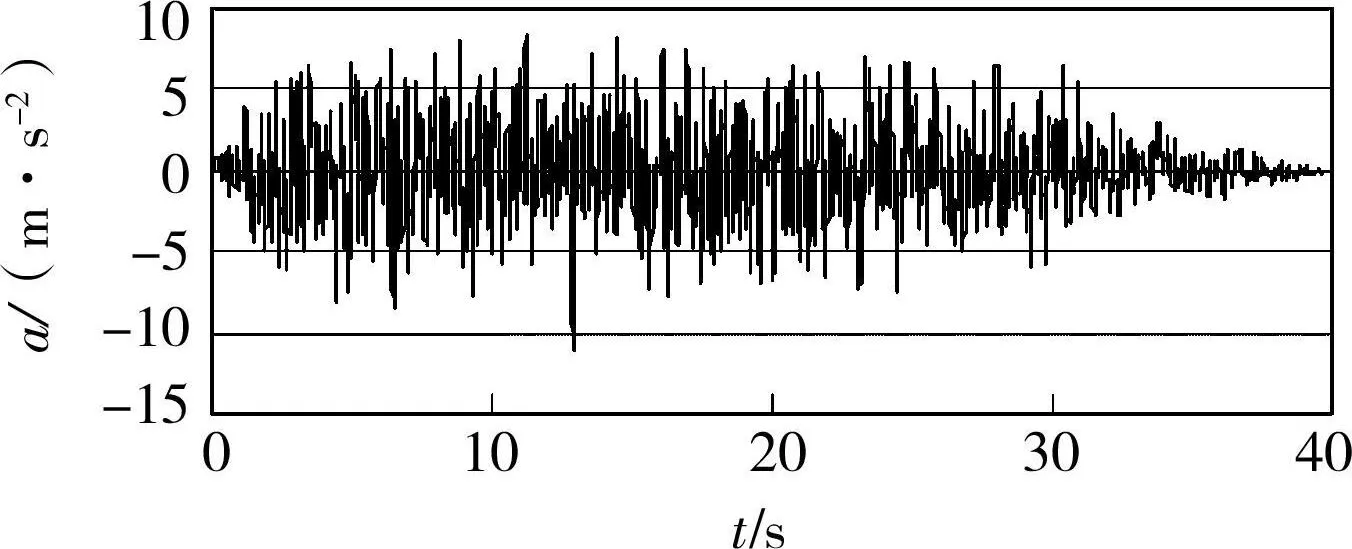
图5 对应III类场地反应谱的某条加速度时程波(加速度峰值 a=1g)

2.3 关键参数的定义

2.3.1 连续梁桥位移延性需求系数 连续梁桥不同于单自由度体系,连续梁桥一般有多个桥墩,地震作用下各桥墩位移延性需求系数一般不同,这里将各墩最大位移延性需求系数μem定义为连续梁桥的位移延性需求系数。其中,连续梁桥的某单个桥墩的位移延性需求系数μe,i按下式计算:

其中,Δy,i为某桥墩屈服位移,Δe,i为对应的弹性反应谱分析的墩顶位移。需要注意,Δe,i可能不是墩顶的真实位移(对于符合等位移准则的桥梁,Δe,i近似为墩顶的真实位移)。

2.3.2 主要振型的最小周期 与单自由度体系不同,连续梁桥的动力响应受一阶或多阶振型控制,并对应不同的自振周期。若连续梁桥前几阶振型的振型质量参与系数之和超过90%,则将这几阶振型的最小周期定义为主要振型的最小周期 Tmin。通过改变参数,上述绝大部分连续梁桥由两阶或两阶以上主要振型控制,为非规则梁桥,若某座桥梁前两阶振型周期分别为0.9 s、0.5 s,相应的振型质量参与系数分别为60%、35%,则此桥的Tmin为0.5 s;少部分连续梁桥仅由一阶主要振型控制,对应振型质量参与系数超过了90%,为规则梁桥,该主要振型的周期即为主要振型的最小周期Tmin。

2.4 分析结果

在进行弹性反应谱分析和非线性时程分析时,反应谱与加速度时程相对应(即非线性时程分析采用对应场地反应谱所生成的7条加速度时程波作为地震动输入,取位移反应平均值与弹性反应谱分析的位移反应相比较)。对于每座桥梁的同一节点,将非线性时程分析与弹性反应谱分析的位移需求的比值定义为该桥梁的位移修正系数C。

对于每座连续梁桥,调节地震动加速度峰值使对应的连续梁桥的位移延性需求系数μem大致为1.5、3.0和6.0,桥台、墩顶处主梁节点对应的位移修正系数C如图6(a)-(c)所示,其中,横坐标为每座连续梁桥主要振型的最小周期 Tmin。同时,为了方便与单自由度体系等位移准则对比,将连续梁桥的位移延性需求系数 μem分别代入式(3)和式(4),并将结果绘于相应图中。

根据图6,得到以下规律:

1)连续梁桥的位移修正系数C的总体变化趋势与单自由度体系位移修正系数曲线相似;

2)对于相同的μem,Tmin越短,连续梁桥的位移修正系数C相对于单自由度体系位移修正系数曲线的离散性越大,反之,离散性越小;

3)对于相同的Tmin,μem越大,连续梁桥的位移修正系数C相对于单自由度体系位移修正系数曲线的离散性越大,反之,离散性越小;

4)对于不同的 μem,只要 Tmin≥T l,绝大部分连续梁桥的位移修正系数C分布在0.8～1.2。

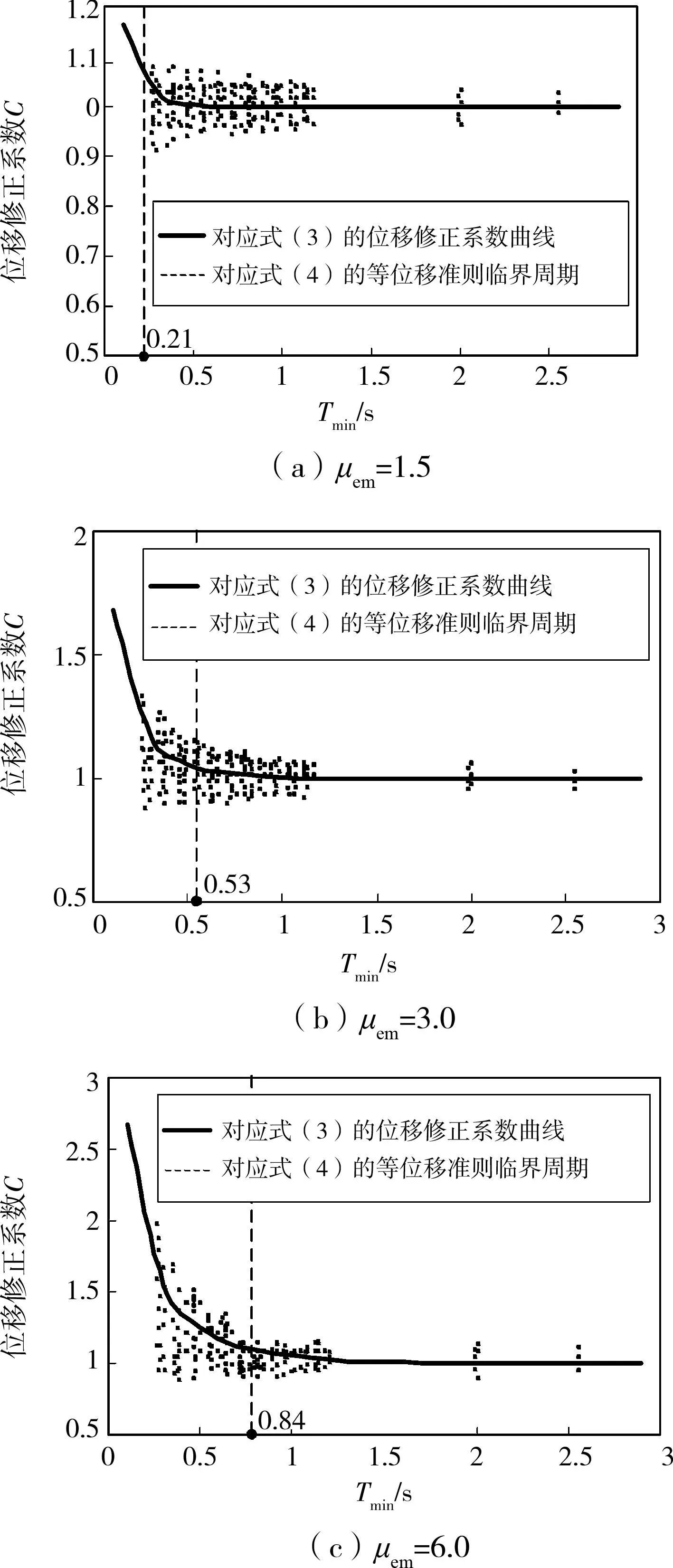
图6 不同μem的连续梁桥的位移修正系数C

上述规律说明,对于连续梁桥横桥向,只要Tmin≥T l,桥梁弹性位移与弹塑性位移近似相同,等位移准则仍然适用;由于连续梁桥为多自由度体系,这里称之为多自由度体系等位移准则。根据以上分析,对多自由度体系等位移准则具体应用条件进行总结,见图7。

图7 多自由度体系等位移准则应用条件

虽然Miranda提出的单自由度体系的位移修正系数C仅是基于264条“硬场”加速度时程波记录的回归结果,并且这里的多自由度体系等位移准则是在此基础上的向多自由度体系的概念延伸,但是参数分析结果(见图6)表明,规范中的“不同场地”的地震动输入对多自由度体系等位移准则的影响很小,或者说多自由度体系等位移准则适用于规范中的各种场地。

连续梁桥是否满足多自由度体系等位移准则,取决于主要振型最小周期 Tmin与临界周期 Tl的大小比较,其中,Tmin只与结构本身有关,而 Tl与结构在地震下的各墩最大位移延性需求系数μem有关。所以,对于一座特定的连续梁桥,在较小的地震作用下,可能会满足多自由度体系等位移准则,而在较大的地震作用下,则可能不满足多自由度体系等位移准则。

一般情况下,连续梁桥越不规则,主要振型越多,主要振型最小周期 Tmin越小。如果不同非规则程度的连续梁桥在各自的地震作用下达到了相同的μem(即临界周期T l相同),非规则程度较小的连续梁桥可能满足多自由度体系等位移准则,而非规则程度较大的连续梁桥则可能不满足多自由度体系等位移准则。因此,在其它因素相同的情况下,连续梁桥的非规则程度越大,多自由度体系等位移准则成立的条件则显得越苛刻。

3 连续梁桥横桥向简化抗震设计

3.1 简化抗震设计步骤

连续梁桥的基于位移的抗震设计主要包括结构目标位移的确定、结构位移需求预计以及结构目标位移与位移需求的平衡迭代等主要步骤。如果桥梁满足多自由度体系等位移准则,采用相对简单的弹性分析方法(如弹性反应谱分析)计算得到的弹性位移需求可以用来近似代表桥梁结构的弹塑性位移需求,较大程度上简化了地震作用下桥梁结构的位移需求的预计,进而简化了连续梁桥的基于位移的抗震设计。

采用多自由度体系等位移准则的基于位移的简化抗震设计步骤如下:

1)确定各墩墩顶主梁节点目标位移Δc,i,i表示桥墩编号。

2)初步确定桥墩截面尺寸和截面纵筋配筋率,桥墩截面尺寸可暂时按照恒载作用下轴压比15%确定,截面纵筋配筋率可暂时取为1%。

3)建立桥梁弹性模型(桥墩截面抗弯刚度采用有效刚度),并进行动力特性分析和弹性反应谱分析,得到主要振型最小周期Tmin和各墩顶主梁节点弹性位移需求 Δe,i,然后计算各墩最大位移延性需求系数μem,并代入式(4),求得多自由度体系等位移准则临界周期Tl。

4)如果Tmin≥T l,桥梁满足多自由度体系等位移准则,Δe,i可近似作为桥梁结构的位移需求。

5)如果0.95≤max(Δe,i/Δc,i)≤1.05,认为桥梁满足设计目标,进入步骤(6);否则,桥墩截面有效抗弯刚度乘以max(Δe,i/Δc,i),回到步骤(3)重新计算。

6)根据桥墩截面有效抗弯刚度,对桥墩进行具体设计,包括截面尺寸和配筋。

7)最后根据桥墩能力和能力保护原则,对基础、支座和其它构件进行设计。

3.2 算例

为了更好的说明上述设计步骤,采用多自由度体系等位移准则对一座连续梁桥横桥向进行详细抗震设计。已知条件如下:主梁和跨径分布同表1;墩高分布为8m、14m、8m;桥墩混凝土采用 C30,纵筋采用HRB335;地震动输入采用公路工程抗震设计规范(JTJ 004-89)中的III类场地反应谱,加速度峰值为0.4 g;其它方面同2.1中的研究假定。桥墩墩顶主梁节点目标位移本应该根据桥墩的允许损伤程度具体计算,但由于研究重点在于位移需求的简化预计,桥梁的各墩墩顶主梁节点目标位移被简单假定为相应桥墩高度的1.0%。桥梁具体抗震设计步骤见表2。

表2 采用多自由度体系等位移准则的基于位移的简化抗震设计步骤

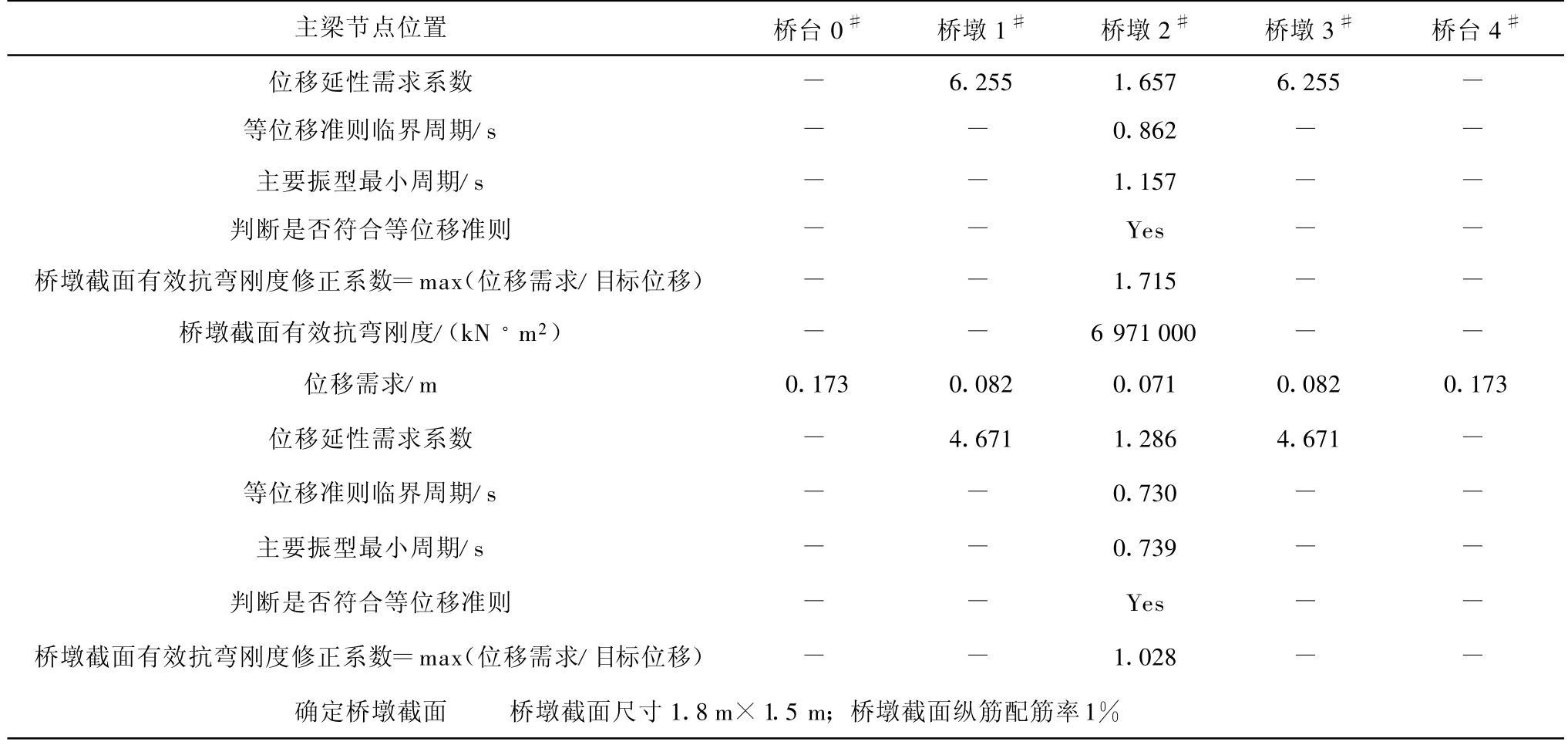
续表2

表2中,按照恒载作用下轴压比15%初步确定的桥墩截面尺寸为1.5m×1.5m,截面纵筋配筋率取为 1%,对应的桥墩截面有效抗弯刚度为4 064 262 kN◦m2,初次计算得到各墩墩顶主梁节点位移需求与目标位移的最大比值max(Δe,i/Δc,i)=1.715,说明桥墩墩顶主梁节点位移需求明显大于目标位移,桥墩截面有效抗弯刚度应该增加。桥墩截面有效抗弯刚度由 4 064 262 kN◦m2乘以max(Δe,i/Δc,i),增加到 6 971 000 kN ◦m2,然后计算得到max(Δe,i/Δc,i)=1.028,位移需求近似等于目标位移,满足0.95≤max(Δe,i/Δc,i)≤1.05的条件,可以根据桥墩截面有效刚度6 971 000 kN◦m2对桥墩截面进行设计。最后根据桥墩能力和能力保护原则,对基础、支座和其它构件进行设计,此处省略。

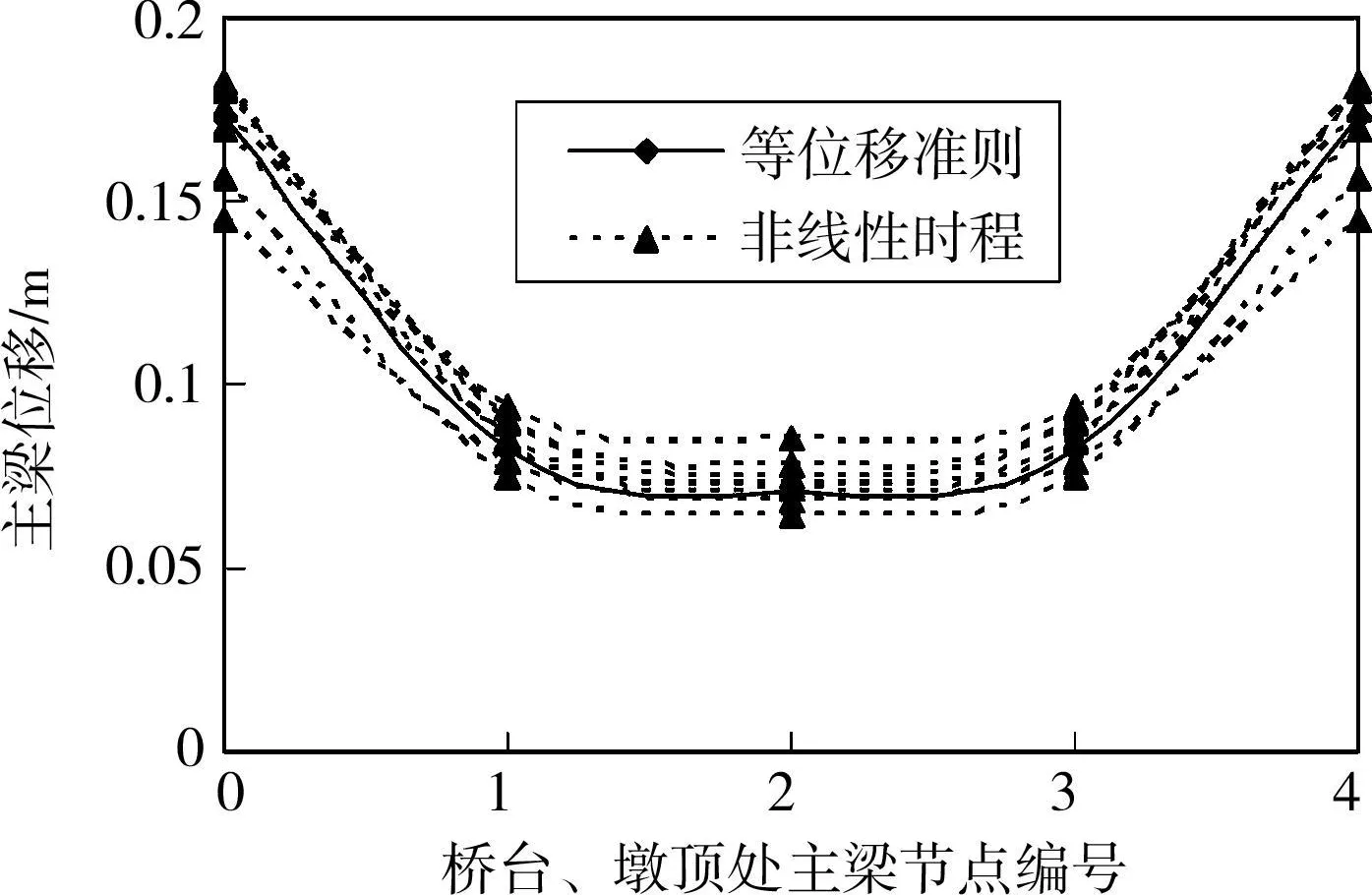
图8 非线性时程分析与等位移准则分析的主梁位移需求对比

为了验证设计结果的合理性,采用非线性时程分析计算最终设计方案,地震动输入采用图5中的7条时程波,加速度峰值调至0.4g。采用多自由度体系等位移准则和非线性时程分析分别得到的主梁位移需求如图8所示,其中主梁节点编号同图3。从图8看出,采用多自由度体系等位移准则确定的主梁位移需求与非线性时程分析得到的主梁位移需求比较接近。

4 结论

在分析单自由度体系等位移准则的基础上,以4跨连续直桥为背景,采用非线性时程分析和弹性反应谱分析分别计算了地震作用下桥梁横桥向的弹塑性位移需求和弹性位移需求,并对两者的比值进行了统计分析,提出了多自由度体系等位移准则的概念,并将多自由度体系等位移准则应用到了连续梁桥横桥向的基于位移的简化抗震设计。主要得到以下结论:

1)多自由度体系等位移准则的临界周期主要与各墩最大位移延性需求系数相关,各墩最大位移延性需求系数越大,多自由度体系等位移准则的临界周期越长;

2)当连续梁桥的主要振型的周期都大于或等于对应的多自由度体系等位移准则的临界周期时,非线性时程分析得到的弹塑性位移需求与弹性反应谱分析得到的弹性位移需求比较接近,满足多自由度体系等位移准则;

3)对于满足多自由度体系等位移准则的连续梁桥,可以采用相对简单的弹性分析方法(如弹性反应谱分析)近似计算结构的位移需求,较大程度上简化了地震作用下桥梁结构的位移需求的预计,进而简化了连续梁桥的基于位移的抗震设计。

在进行参数分析和算例分析时,选取的桥梁模型比实际桥梁简单,这主要是为了更加直观地揭示规律,多自由度体系等位移准则理论上同样适用于结构复杂的实际连续梁桥。该文仅从抗震设计角度上分析,未验证所选桥梁模型能否满足自重、抗风、船撞、稳定等要求;在实际工程应用时,需要将文中的抗震设计方法与其它因素相结合使用。

对于墩高不同的桥梁,假定各桥墩具有相同的截面,这在现实中是常见的,很多学者在做研究时也采用了这样的假定[2,14]。但是,如果根据墩高不同而设置不同的桥墩截面,是否更优也非常值得研究。

[1]American Association of StatEHighway and Transportation Officials.AASHTO LRFD BridgEDesign Specifications [S].Washington D C,USA,2007.

[2]陈亮,李建中,张文学.梁墩刚度分布对连续梁桥横桥向规则性的影响[J].同济大学学报:自然科学版,2007,35(9):1175-1180.CHEN LIANG,LI JIAN-ZHONG ZHANG WENXUE.Effects of girder and pier stiffness on continuous bridgEregularity in transversEdirection[J].Journal of Tongji University:NaturEScience,2007,35(9):1175-1180.

[3]黄建文,朱晞.以位移为基础的钢筋混凝土连续梁桥抗震设计方法[J].中国公路学报,2005,18(2):28-33.HUANG JIAN-WEN,ZHU XI.Displacement-based seismic designmethod for RCcontinuous girder bridges[J].China Journal of Highway and Transport,2005,18(2):28-33.

[4]MWAFY A,ELNASHAI A,YEN W H.Implications of design assumptions on capacity estimates and demand predictions ofmultispan curved bridges[J].Journal of BridgEEngineering,2007,12(6):710-726.

[5]PIINHO R,CASAROTTI C,ANTONIOU S.A comparison of single-run pushover analysis techniques for seismic assessment of bridges[J].EarthquakEEngineering and StructurEDynamics,2007,36(10):1347-1362.

[6]ISAKOVIC T,LAZAROm PN,FISCHINGERm.Applicability of pushovermethods for thEseismic analysis of single-column bent viaducts[J].EarthquakEEngineering and StructurEDynamics,2008,37(8):1185-1202.

[7]PARASKEVA T S,KAPPOS A J,SEXTOS A G.Extension ofmodal pushover analysis to seismic assessment of bridges[J].EarthquakEEngineering and StructurEDynamics,2006,35(10):1269-1293.

[8]AYDINOGLUm N.An improved pushover procedurEfor engineering practice:incremental responsEspectrum analysis IRSA[C]//Proceedings of thEInternational WorkshoPPerformance-Based Seismic Design Concepts and Implementation,Bled,Slovenia,2004:345-356.

[9]RIDDELL R,HIDALGO P,CRUZ E.Responsemodification factors for earthquakEresistant design of short period structures[J].EarthquakESpectra,1989,5(3):571-590.

[10]MIRANDA E.Inelastic displacement ratio for structures on firm sites[J].Journal of Structural Engineering,2000,126(10):1150-1159.

[11]郭磊.桥梁结构基于位移的抗震设计方法研究[D].上海:同济大学,2006.

[12]王光远.结构动力学[M].北京:高等教育出版社,2006.

[13]CHOPRA A K,GOEL R K.Amodal pushover analysis procedurEfor estimating seismic demands for buildings[J].EarthquakEEngineering and Structural Dynamics 2002,31(3):561-582.

[14]ISAKOVIC T,FISCHINGERm.Highermodes in simplified inelastic seismic analysis of singlEcolumn bent viaducts[J].EarthquakEEngineering and StructurEDynamics,2006,35(1):95-114.

[15]FAHJAN Y,OZDEM IR Z.Scaling of earthquakEaccelerograms for non-linear dynamic analysis tomatch thEearthquakEdesign spectra[C]//ThE14th World ConferencEon EarthquakEEngineering,Beijing,China,2008.