具有年龄结构的SI传染病模型的分析

张 剑，张宏民

（齐齐哈尔大学理学院，黑龙江 齐齐哈尔 161006）

近几年来，随着SARS，甲型H1N1等众多新型传染病的出现，使得人们对于传染病的研究又加以关注。传染病的防治是关系到人类健康和国计民生的重大问题，对疾病流行规律的定量研究是防治工作的重要依据，根据疾病的发生、发展及环境变化等情况，建立能反映其变化规律的数学模型，通过模型动力学性态的研究来显示疾病的发展过程，预测其流行规律和发展趋势，分析疾病流行的原因和关键因素，寻求对其进行预防和控制的最优策略，为人们防治决策提供理论基础和数量依据。由此可见，研究种群的传染病模型对于种群的生存与发展是至关重要的。众多研究考虑了疾病在食饵之间传播的模型，得到疾病流行的阈值条件[1]。分析了捕食者具有疾病的SI模型，讨论了解有界性和平衡点全局稳定性[2]。并分别对具有年龄结构的SEIR和SIS传染病模型进行了分析[3-4]。但对具有年龄结构的单种群模型，在成年种群染病的SI问题尚未讨论过。本文根据成年和幼年种群不同的生长特性，以及疾病对不同年龄结构的两种群的影响，发展规律和传播特性等因素研究该类模型，进而可以显示疾病的发展过程，揭示其流行规律，为人们防治决策提供理论基础。

1 模型的建立与假设

具有年龄结构的传染病模型如下：

其中，x表示幼年种群数量；s表示易感的成年种群数量；I表示染病的成年种群数量；α表示幼年种群的出生率；r1、r2、r3分别表示幼年种群、易感的成年种群、染病的成年种群的死亡率；η表示幼年种群的密度制约系数；β表示幼年种群向成年种群的转化率；b表示接触率。

根据模型的生态意义，本文在

R3+=上讨论。

根据模型的实际背景作如下假设：①假设疾病只在成年种群间传播。②不考虑种群的流动性。③成年种群患病后不能够治愈；患病后一旦与易感染者接触即具有一定的传染率。

2 模型平衡点的存在性

定理1模型（1）的平衡点存在的条件：

证明：模型（1）的平衡点是满足下面方程组的解。

根据方程组（2）可知模型（1）存在三个平衡点分别是E0（0，0，0），E1（x0，s0，0）和唯一的正平衡点E2（x*，s*，I*）。

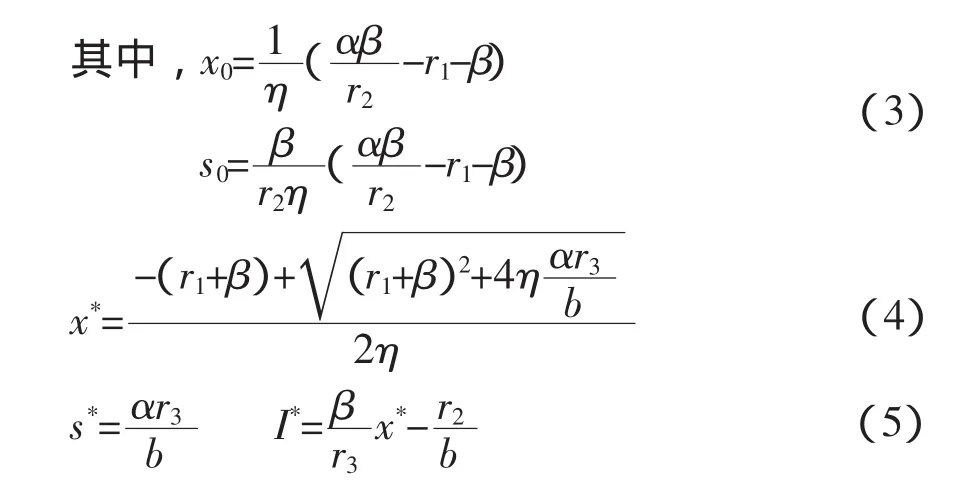
根据模型的实际生态意义知（3），（4），（5）各式应恒大于0，因此得到模型（1）的平衡点存在的条件是：

3 平衡点的稳定性

定理2当αβ-r2（r1+β）＜0时，模型（1）的平衡点E0是局部渐近稳定的；当αβ-r2（r1+β）＞0时，平衡点E1是局部渐近稳定的。

证明：模型（1）的Jacobi系数矩阵为

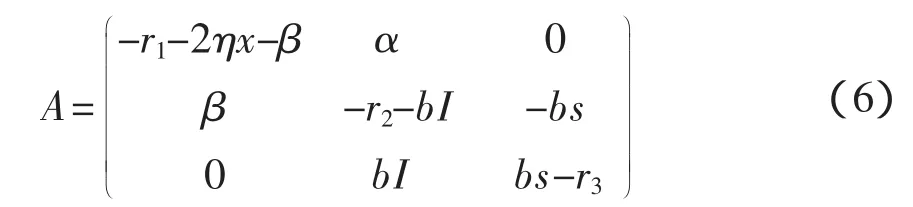
下面分别平衡点E0和E1的稳定性进行讨论。

平衡点E0（0，0，0）的系数矩阵是

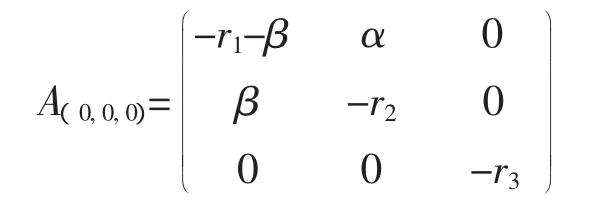
而其对应的特征方程是

特征根是 λ1=-r3＜0

平衡点E1（x0，s0，0）的系数矩阵是

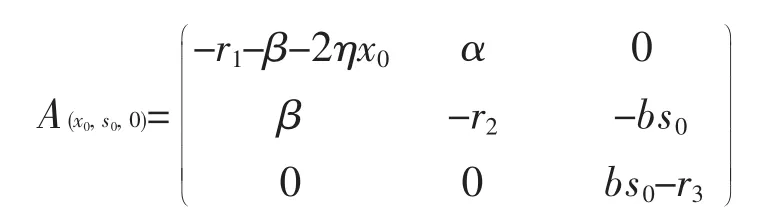
而其对应的特征方程是

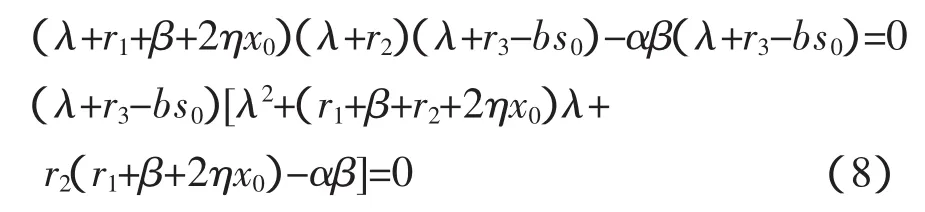
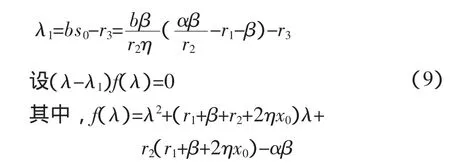
f（0）=αβ-r2（r1＋β）＞0（由E1的存在性知）则λ2，λ3是两个具有负实部的特征根。

证明：E2（x*，s*，I*）的系数矩阵是

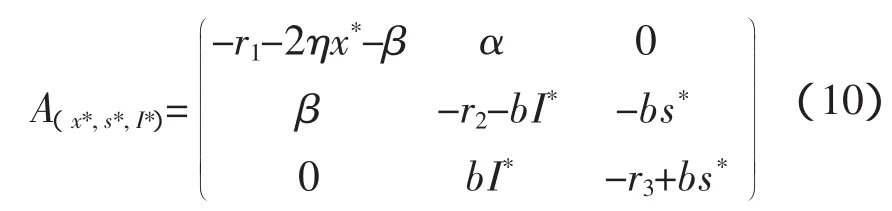
特征方程为 λ3+A1λ2+A2λ+A3=0

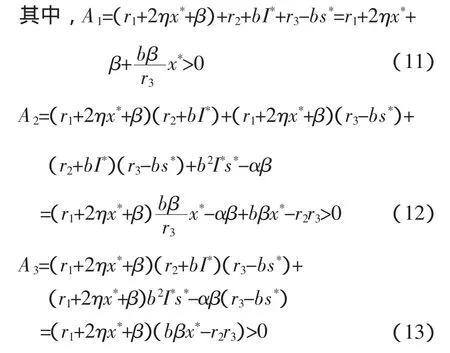
由 E2的存在性知 A1＞0，A2＞0，A3＞0。

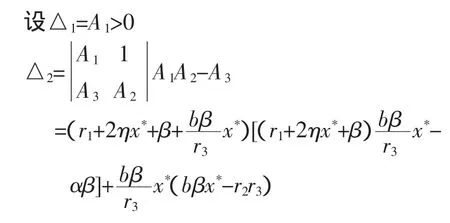
由 E2存在，知 bβx*-r2r3＞0

由 A2＞0 知

△3=A3△2＞0。

根据Hurwitz判别法知，点E2对应的特征方程所有特征根均有负实部，故平衡点E2局部渐近稳定。因此只要正平衡点E2存在，其必定是局部渐近稳定的平衡点。

4 模型试验验证

5 结 论

本文所研究的具有年龄结构的SI传染病模型，是将生物个体按其生理年龄进行分类，以便更好地反映个体的生理特征和影响疾病传播方面的差异，在疾病在成年种群间传播的假设条件下，得到平衡点的局部稳定性。，E2是局部渐近稳定的。说明此时，模型的唯一正平衡点存在且局部稳定，也就是说疾病不会造成两个年龄结构的种群的灭绝。该模型可以用来解释在假设条件下的生物种群在疾病的发生及种群内的传播等因素，通过对模型动力学性态的定性、定量分析，能够揭示其发展变化趋势，分析疾病流行的原因和关键因素，寻求对其预防和控制的最优策略。人们可以利用该结论，创造良好的环境，使得疾病在生物种群中不造成较大的影响，不会造成种群的灭绝。这类模型在描述与年龄有关的疾病的传播规律时将更加有效和实用。本文的研究结果，对于生物部门控制疾病在生物种群间的传播具有一定的参考价值。

[1]Chattopad J,Arino O.A predator-prey model with disease in the prey[J].Nonlinear Anal,1999,36∶749-766

[2]张江山,孙树林.捕食者有病的生态流行病模型的分析[J].生物数学学报,2005,20(2)∶157-164.

[3]王定江.时变年龄结构的SEIR传染病模型解的存在性[J].数学的实践与认识,2003,33(8)∶91-96.

[4]EI-Doma M.Analysis of an age-dependent SIS epidemic model with vertical transmission and proportionate mixing assumption[J].Math Comput Model,1999,29∶31-43.

[5]王静,王克.具有年龄结构的单种群模型单一捕获的优化问题[J].东北师范大报∶自然科学版,2003,35(2)∶1-6.

[6]陈兰荪.数学生态学模型与研究方法[M].北京∶科学出版社,1988∶156-172.

[7]Li Y F,Wang W.Characteristics of monoclonal antibody against infectious bursal disease virus[J].Journal of Northeast Agricultural University∶English Edition,1999,6(2)∶128-132.

[8]张剑,张宏民,丁丽英.捕食-食饵系统的捕获优化问题[J].东北农业大学学报,2007,38(3)∶384-386.

[9]李益群,任谨慎,李建全.一类带有一般出生率的SIS传染病模型的全局分析[J].数学的实践与认识,2009,39(23)∶176-181.

[10]陈庚.一类具有年龄结构的传染病模型的持续性质[J].高校应用数学学报∶A 辑,2007,22(3)∶253-262.

[11]何泽荣,雒志学.一类带接种和年龄结构的流行病模型分析一类带接种和年龄结构的流行病模型分析[J].工程数学学报,2003,20(2)∶41-45.

[12]王晓燕,杨俊元.具有Logistic增长和年龄结构的SIS模型[J].数学的实践与认识,2007,37(15)∶99-103.

[13]田灿荣.一类具常数接触率传染病模型的稳定性分析[J].生物数学学报,2009,24(1)∶47-56.

[14]Allen L J S,Burgin A M.Comparison of deterministic and stochastic SIS and SIR models in discrete time[J].Mathematical Biosciences,2000,163∶1-33.

[15]DiekmannO,Gyllenberg M.On the formulati on and analysis of general deterministic structured population modelsⅡ.Nonlinear theory[J].Math Biology,2001,43(2)∶157-189.