基于时间调制的光学相关法测量亚像元像移研究

樊 超，孙宁宁， 梁义涛，王 锋

(河南工业大学信息科学与工程学院，郑州 450001)

0 引言

1966年C S Weaver和J W Goodman首次提出利用光学方法实现两个函数的卷积运算，与匹配滤波相关器相比，这种联合变换相关器(JTC)具有无需综合滤波、高空间带宽积、高调制度、低载频及可实时操作等优点［1］。近年来，由于空间光调制器(SLM)和CCD等实时光电器件的发展，使得联合变换相关器从纯光学系统发展到计算机控制的光电混合系统，既有光学的并行处理、大容量和高速度的优点，又有计算机处理的灵活可编程性。这些优良特性使其具有广泛的实际意义和应用前景，例如军事上空间制导、目标跟踪，工业上机器视觉、自动化检测及图片处理，医学上恶性肿瘤细胞识别等［2－4］。目前，国内外很多学者致力于研究其在图像模式识别方面的不同应用，并提出了改善识别准确率的各种图像处理方法［5－10］。本文将联合变换相关器应用于亚像元像移测量，通过在飞行器上对地面景物进行高帧频连续拍摄(或在地面对运动目标进行高帧频拍摄)，得到一系列时序图像，将相继拍摄到的两帧图像使用JTC进行光学相关运算，测量出图像间的亚像元像移，而后采用图像处理的方法，根据测量的像移量对图像进行配准，改善图像的信噪比，提高成像质量，同时还可测量出飞行器(或运动目标)的运动参数。

1 联合变换相关器测量像移的原理

这里采用结构相对简单、紧凑的单透镜、单空间光调制器(SLM)的联合变换相关器，如图1所示。中心点分别位于(0，a)、(0，－ a)的参考图像 r(x，y)和目标图像t(x，y)同时对称地读入SLM，并且和参考图像相比，目标图像的景物沿x方向和y方向分别移动了Δx、Δy，则相关器的输入E(x，y)可表示为

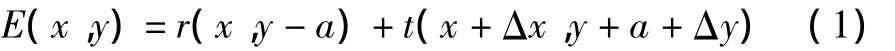
该输入经过一次傅里叶变换后，得到的频谱函数G(u，v)为

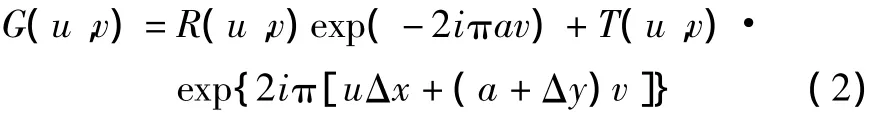
这里，R(u，v)和 T(u，v)分别为 r(x，y)、t(x，y)的傅里叶变换。该频谱复振幅分布经平方律转换器转换成联合变换功率谱分布:

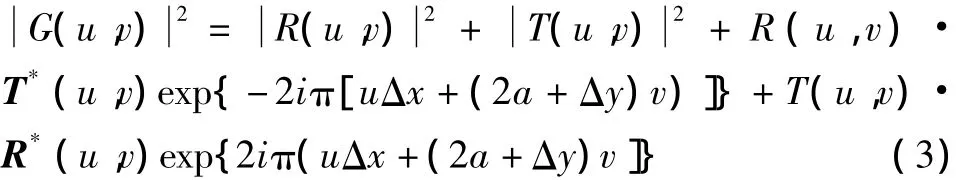
式中上标*表示复共轭。在数字处理与控制单元的控制下，联合变换功率谱重新送入SLM中，再经过一次傅里叶变换后，得到相关输出为

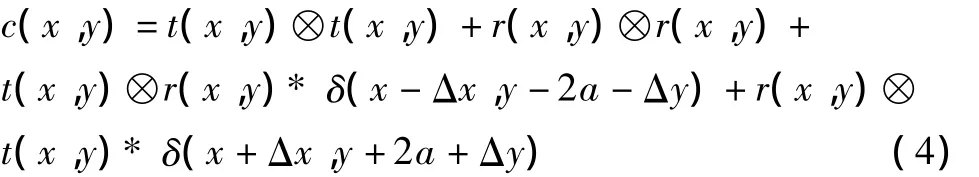
式中:*表示卷积;⊗表示相关运算。前两项为自相关项，后两项为互相关项。从上式可以看出，互相关信号中包含了像移信息Δx、Δy，只要测出互相关峰相对于理想位置(0，±2a)的偏移量，就可以得到所要探测的像移值。

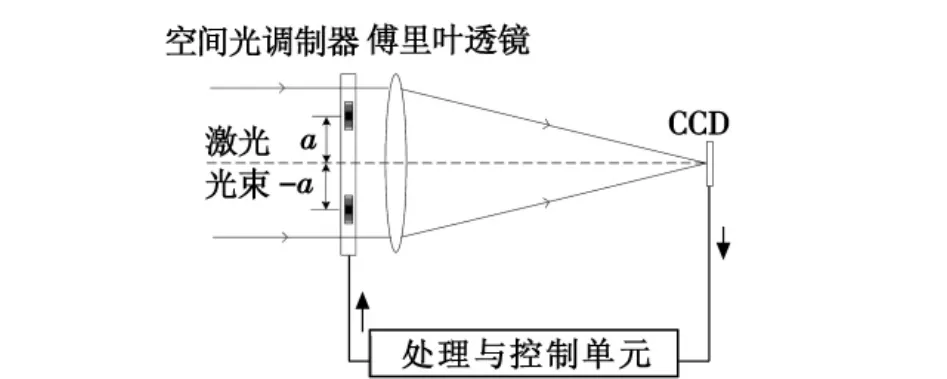
图1 光电混合JTC结构图Fig.1 Structural scheme of optoelectronic JTC

2 基于时间调制的JTC测量亚像元像移的实验研究

根据单透镜联合变换相关器原理，采用的实验光路结构如图2所示。图中，激光光源经衰减、扩束后平行照射空间光调制器，输入图像经傅里叶透镜变换后由CCD采集其功率谱，然后由计算机对该功率谱进行处理后再送入空间光调制器，经傅里叶透镜变换后由CCD得到相关图像。这里，所使用的空间光调制器(SLM)是英国CRL公司生产的XGA3型电寻址TFTLCD，其空间分辨率为1024×768，像元间距18μm×18μm，像元尺寸13μm ×10μm。使用的 CCD 是意大利DTA公司生产的EL－400ME，其分辨率为768×512，像元尺寸9μm×9μm。当使用He－Ne激光器作为相干光源时，计算得到傅里叶透镜的焦距f=196.6 mm。再根据菲涅耳衍射原理和SLM的面板尺寸，最终选择了相对孔径为1∶5.3的双胶合透镜作为傅里叶变换透镜。由以上器件构成的JTC实验装置如图3所示。

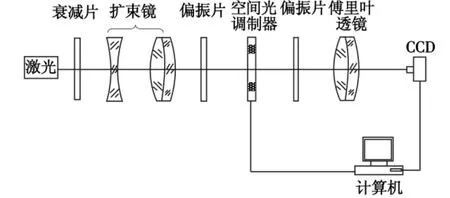
图2 JTC的实验光路图Fig.2 The experimental light route of JTC

图3 JTC实验装置Fig.3 The experimental mounting of JTC

为了模拟亚像元像移，实验中使用的图像如图4所示。对图4中的图像使用像元合并和线性内插的方法得到在x方向和y方向具有亚像元像移，且分辨率下降1/2的像移图像。如果认为原图像以奈奎斯特频率采样的话，那么最终得到的分辨率下降的图像就可以准确模拟出亚像元像移。

图4 实验使用的图像Fig.4 Images used in the experiment

例如，使用上述像移图像产生方法，对图4b产生的两幅像移图像进行相关运算，得到的联合功率谱(JPS)和相关输出分别如图5a、5b。从图5b可以看出，若不对相关器进行任何处理，此时得到的相关峰是具有一定面积的弥散斑，虽然从理论上来说通过测量相关峰之间的间距可以测量两幅图像间的亚像元像移，但是如果对这样的两个弥散斑直接进行测量，实验表明测量误差大于1个像元。引起该问题的主要原因是由于传统联合变换相关存在较强的零级衍射，从而使输出面中相关输出的衍射效率较低，影响相关峰的探测。针对上述问题，这里使用了时间调制的联合变换相关器TM－JTC改善相关峰输出形状，以此提高像移测量精度。

图5 JTC的联合功率谱及相关输出峰Fig.5 The JPS and output of the JTC

时间调制的方法是在JTC的空间光调制器上按一定的时序关系分别加入不同的输入信号，如图6所示，其时序关系见表1。

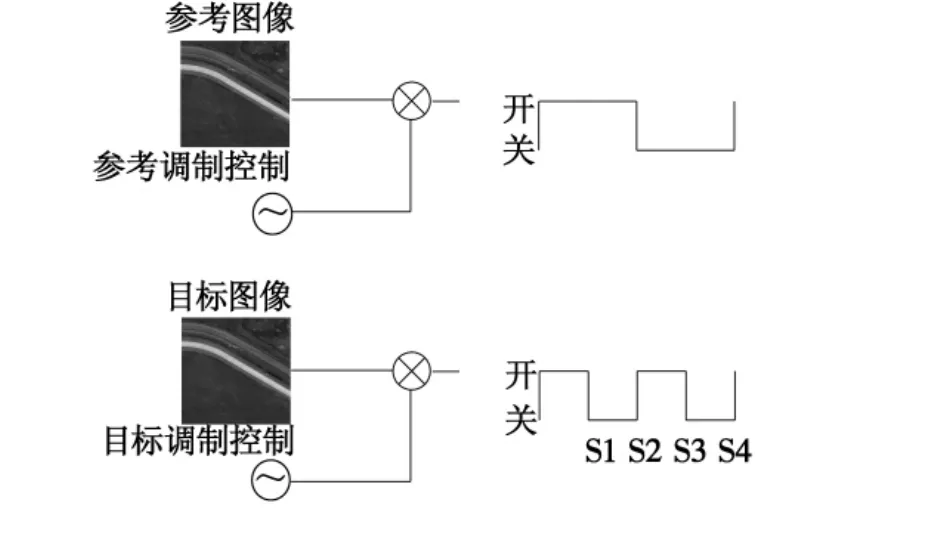
图6 时间调制JTC的输入图像时序关系Fig.6 Sequential relation of the input image of the TM－JTC

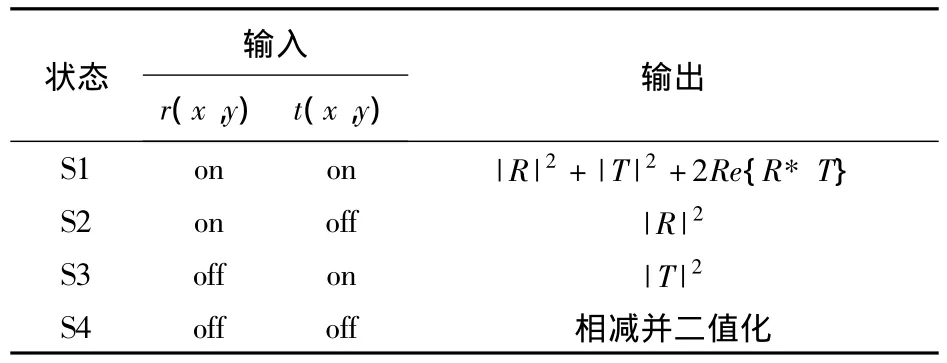
表1 时间调制JTC输入、输出面时序状态表Table 1 Sequential state of the TM－JTC

首先在S1时序内将参考图像r(x，y)和像移图像t(x，y)同时加载到输入面上，此时得到两幅图像的联合功率谱|G(u，v)|2(如式(3))。然后在S2、S3时序内分别将参考图像和目标图像加载到输入面上，得到各自单独的功率谱|R(u，v)|2、|T(u，v)|2。在 S4 时序内将前3个时序得到的功率谱分别相减，得到:

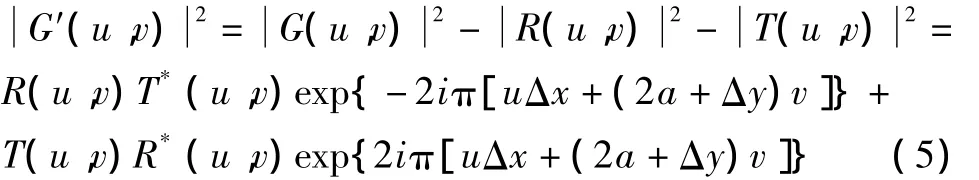
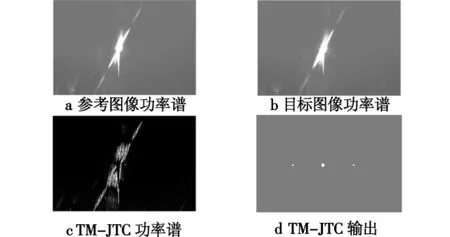
图7 时间调制法得到的功率谱及相关输出Fig.7 The JPS and output of the TM－JTC

从图5、图7可以得到以下结论:1)使用时间调制的方法极大削减了中央零级衍射斑的强度(图7c)，零级衍射斑的削减直接导致相关输出中自相关峰能量的降低。将图7d与图5b比较不难发现，使用该方法后，中央零级自相关峰的能量和尺寸得到有效削减，同时互相关峰收缩为一个边缘清晰、面积较小、强度较高的亮点，这对于像移测量来说是非常有利的。2)比较图5a与图7a、图7b不难发现，联合功率谱的能量分布(图5a)与目标图像或参考图像的功率谱的能量分布形式基本相同，其差别仅在于联合功率谱中包含了大量条纹。由此说明联合功率谱是由参考图像和目标图像上无数对相同点的干涉叠加所构成的，其能量分布受到目标图像(或参考图像)的衍射图像的调制。经过时间调制后，JPS中就只剩下包含像移信息的干涉条纹(图7c)。

使用上述方法对由城市、机场、田地、郊区等不同景物内容的10幅图像构成的像移样本进行了综合测量，由每幅图像随机产生5对大小为128×128像元的像移图像，像移范围在0～60个像元内，构成包含50对不同像移值的测试样本。使用JTC对该样本的像移进行测量，测量结果见图8。

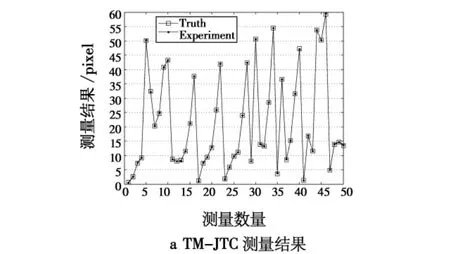
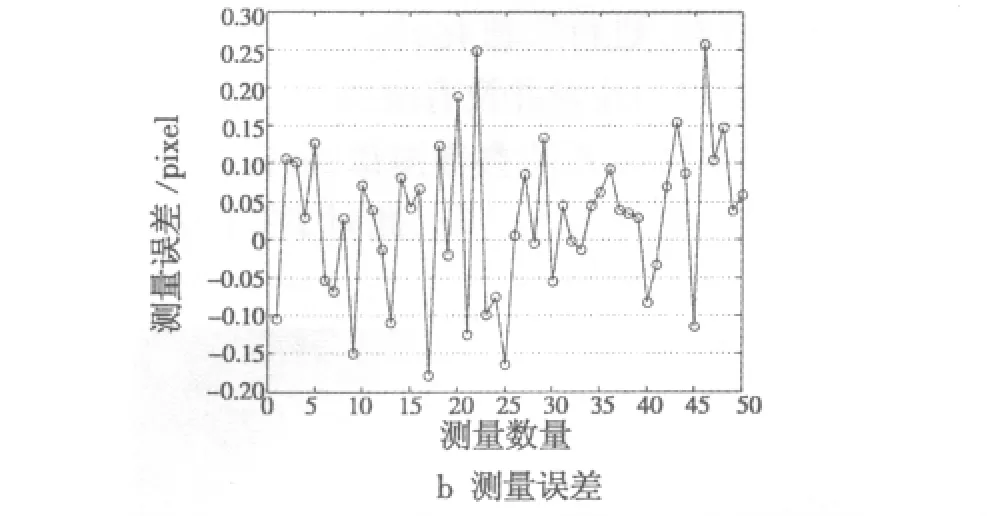
图8 样本测量值与测量误差Fig.8 Measurement results and error of the TM-JTC

利用数理统计的方法对样本测量误差的分布形式、均值和方差分别进行了假设检验，结果表明，使用基于时间调制的联合变换相关法测量像移时，测量误差服从均值为0的正态分布，在显著水平α=0.05情况下，像移测量误差的均方差不大于0.12个像元。

3 结论

基于时间调制的光学联合变换相关法可以对相机以高帧频拍摄到的两幅几乎相同的图像测量出亚像元像移，并且测量精度不随所拍摄景物的内容变化。实验研究表明，在使用该方法测量像移时，测量误差服从均值为0的正态分布，在显著水平为0.05下，像移测量误差的均方差不大于0.12个像元。近年来，随着SLM和CCD等光电器件制作工艺和技术的不断提高，目前已经出现了每秒几千帧的高频空间光调制器和高速CCD相机，这些器件的出现可以实现实时像移测量，使其在高分辨率卫星相机的像移测量和高速摄影方面有着极其广泛的应用前景。

［1］JUTAMULIA S.Joint transform correlators and their applications［C］//SPIE，2005，1812:233-243.

［2］DRAGULINESCU A，COJOC D.Optical correlators:systems and domains of applications［C］//SPIE，2005，5972:59721F-1-59721F-8.

［3］樊超，李英才，易红伟.基于光学相关的空间相机像移测量方法研究［J］.光子学报，2008，37(6):1213-1216.

［4］刘皓淳，王红霞，张瑜，等.基于光学相关的多目标检测［J］. 光学技术，2007，33(增):192-194.

［5］ALAM M S.Optoelectronic techniques for real time pattern recognition［C］//SPIE，2001，4470:53-64.

［6］ALAM M S.Efficient joint transform processor［C］//SPIE，2000，4043:96-107.

［7］PATI G S，SINGH K.Experimental and simulation studies on the performance of binary and gray-valued joint transform correlators under poor illumination conditions and nonoverlapping background noise［J］.Opt Eng，1997，36(7):1918-1929.

［8］LI Chunte，YIN Shizhuo，FRANCIS T，et al.Nonzero-order joint transform correlator［J］.Opt Eng，1998，37(1):58-65.

［9］刘冬梅，沈君愉，王丽君.小波变换在图像相关识别中的应用［J］. 激光技术，2004，28(6):641-644.

［10］WANG Hongxia，HE Junfa，SHENG Zhaoxuan.Optoelectronic hybrid joint transform correlator based on power spectrum subtracting and exponential filtering［C］//SPIE，2005，5642:445-450.