考虑机场容量的作战飞机调配保障需求模型

王莉莉， 陈云翔

(空军工程大学工程学院，西安 710038)

0 引言

未来高技术局部战争，多机种组成混合机群整体作战将成为空军基本作战样式［1］。战时一个机场往往进驻多个机种，每种飞机的起飞、着陆距离，留空时间，保障要求不同，对机场的使用要求也不同。同时，飞机起飞和着陆的过程是一个循环使用机场的过程，飞机等待起飞、起飞、到规定空域执行作战任务、等待返回、着陆，都必须考虑到机场容量的大小。一个机场进驻飞机数量过多，不仅会加大保障难度，而且会降低机场保障能力，从而影响部队飞机出动强度。因此，在作战部署时应充分考虑飞机作战性能和机场保障能力。机场保障能力主要取决于飞机保障资源和机场容量等要素。在飞机保障资源配套齐全的前提下，如何根据作战需求和机场容量，确定机场进驻作战飞机的型号、数量，充分发挥飞机整体作战效能，是调配保障急需解决的问题。

机场容量是指一个机场系统允许进驻或通过的飞机流量的统称，它取决于机场的停机位数量和飞机进驻和离开的流动率，包括跑道容量、滑行道容量和停机坪容量等［2］。为了最大限度地提高战时作战飞机出动强度，顺利完成作战任务，本文提出一种以调配飞机数量最少，混合起降中飞机起飞和着陆容量最大为目标函数的作战飞机调配保障需求模型，解决如何调配和补充各机场作战飞机的型号和数量。

1 基本假设

1)以空军战役中某一机场为研究对象;

2)假设该机场跑道为单跑道，且不考虑不同型号飞机对机场跑道的影响;

3)假设飞机在执行任务、地面保障、停放过程中无飞机数损失，飞机连续出动强度在规定范围内，机场各种保障物资供应充足;

4)假设飞机降落率和起飞率服从泊松分布，平均起飞率为 λd，平均到达率为 λa，飞机平均返航率为λfh;

5)假设该机场执行n个作战任务Fn，且完成作战任务Fj，需要第i型飞机数为Ui(Fj);

6)假设完成作战任务Fj，飞机单位时间内起飞架次为Nqf，着陆架次为Nzl;

7)假设完成作战任务Fj，可供调配的各型飞机数量为Aj。

根据飞机到达间隔时间分布和跑道服务时间分布规律，机场跑道容量问题可以使用排队系统模型［3－4］解决。

2 机场容量计算

2.1 飞机起飞容量计算

根据排队理论，机场跑道起飞服务符合(M/M/1)模型。起飞跑道服务强度为ρqf，机场跑道的平均使用时间为tqf，单位时间内平均能被服务完的飞机数为μqf，且 tqf=1/μqf，每架飞机起飞的放行等待时间为 wqf，飞机起飞等待时间为wqd，飞机在空中排队等待时间为wpd，由排队模型(M/M/1)可以得出起飞时跑道空闲状态的概率和有n架飞机等待起飞的概率为

飞机起飞受着陆飞机影响，如两架相继到达请求着陆的飞机之间发生空档，且相继着陆两架飞机之间足够地面飞机起飞，根据放飞情况，飞机起飞放行等待时间wqf也可以写为

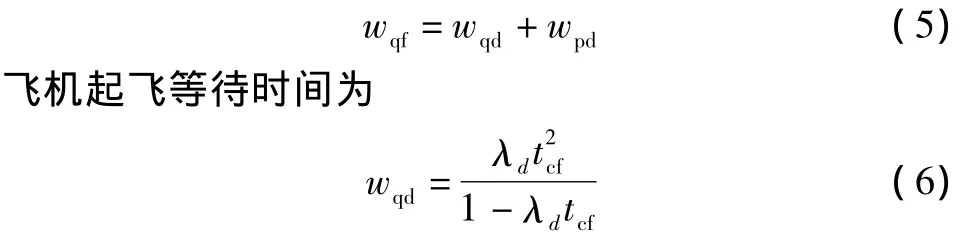
起飞飞机空中排队等待时间为

式中:tcf表示相继起飞的飞机平均间隔时间;tf表示不能放行的起飞飞机平均间隔时间;g表示两架相继到达飞机之间发生空档平均率。

该机场在战时作为起飞降落同时进行的混合使用机场，则平均返航率λfh为

式(5)可以表示为

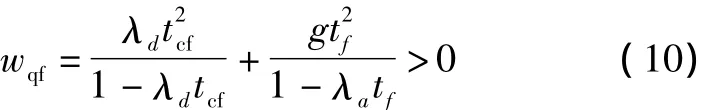
对式(10)进行求导，得出:

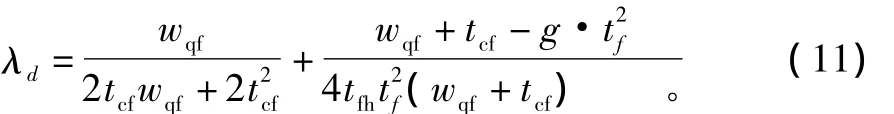
由上可知，战时混合起降中机场跑道满负荷运行时，该机场跑道的起飞极限容量为

2.2 飞机着陆容量计算

由于我军作战飞机性能限制，其着陆容量也有限制。设最大着陆容量为N′zl，排队等待着陆的飞机数量为N′zl－1，根据排队理论，机场着陆服务符合(M/M/1(N))模型。

着陆跑道服务强度为ρzl，机场跑道的平均使用时间为tzl，单位时间内平均能被服务完的飞机数为μzl，每架飞机着陆的放行等待时间为wzl，飞机在空中排队等待时间为w′pd，由排队模型(M/M/1(N))可以得出着陆时跑道空闲状态的概率和有n架飞机等待着陆的概率为

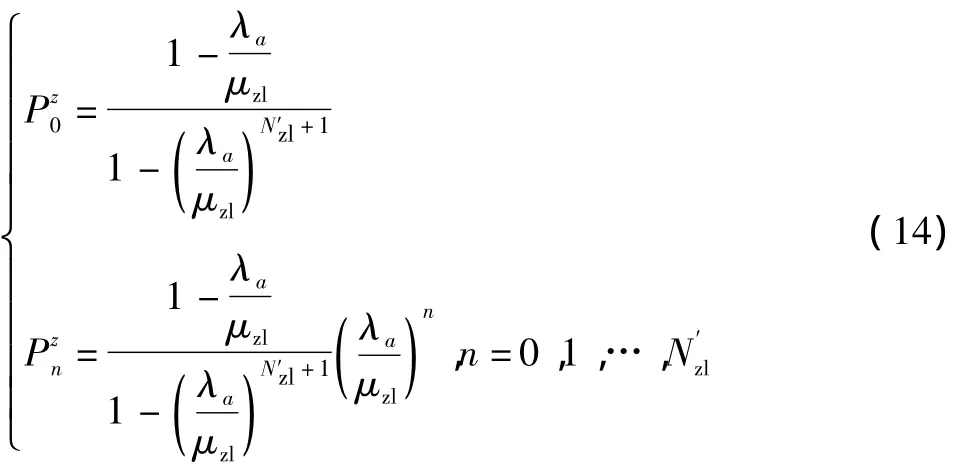
机场跑道着陆服务强度为

飞机空中排队数量为

现假设飞机着陆时在空中等待的最大时间［5］为tmax，那么要求 wzl≤tmax。简化式(18)得:

对式(20)两边求导，并令左边等于0，得出该机场跑道的着陆极限容量为

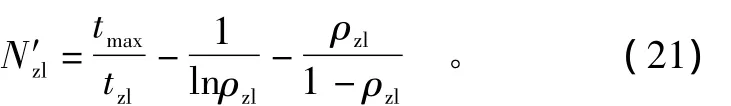
3 机场容量约束下的作战飞机调配保障需求模型

根据假设和推导出的机场跑道单位时间内所能容纳的最大飞机数，可知战时条件下的作战飞机调配数，确保作战任务的顺利遂行。

3.1 约束条件

1)机场容量约束。

该机场跑道起飞的最大容量和着陆最大容量有限制，起飞和着陆的飞机架次不能大于机场最大容量

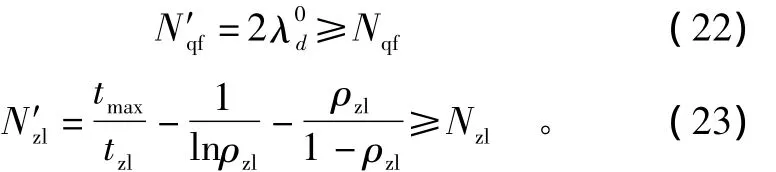
2)数量约束。

执行任务［6］的作战飞机数量不大于可调配数量

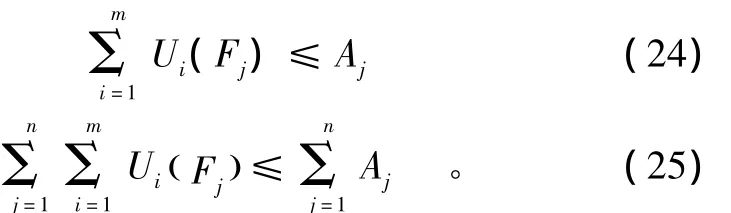
3.2 数学模型

1)使调配飞机数量最少。(考虑飞机种类不同，起降的批次有所不同)

2)使混合起降中飞机起飞和着陆容量达到最大

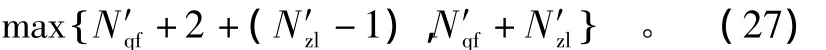
4 实例分析

空军某单位执行演习任务，进驻某机场，试计算该机场最大进驻飞机数。

在执行任务中测量得到相关数据如表1和表2所示。

表1 演习飞行中观测数据Table 1 Observations in flight exercise

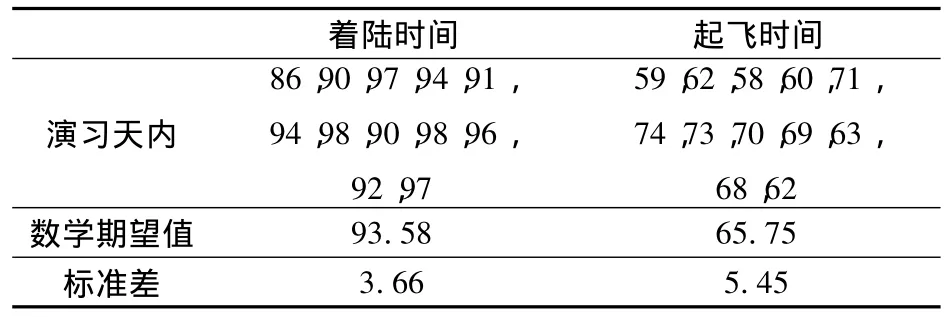
表2 几组飞行起降平均占用跑道时间数据Table 2 Average runway occupancy time of several groups of flight in taking off/landing

根据实际情况，为求得飞机连续起飞时机场跑道的极限容量，选取tf=3 min，即允许连续放飞飞机的最小时间间隔为3 min，参考表1可以得出两组相随出发的飞机平均最小时间间隔tcf=5 min。

1)计算跑道起飞容量。

由于飞机到达率λa服从泊松分布，则地面飞机能正常起飞的平均率g为

根据式(13)，在混合起降中机场跑道满负荷运行时，该机场跑道的起飞极限容量为=20架次/h。

2)计算跑道着陆容量。

假设飞机空中最大等待时间tmax=30 min，根据表1和表2中数据，代入式(21)，计算该机场跑道的着陆极限容量为N′zl=19.97。取整数得空中排队的最大着陆容量为N′zl=20架次/h。

根据式(27)，该机场混合起降过程中，跑道的极限容量为40架次/h。

图1所示为该机场跑道最大起飞和着陆容量的示意关系。

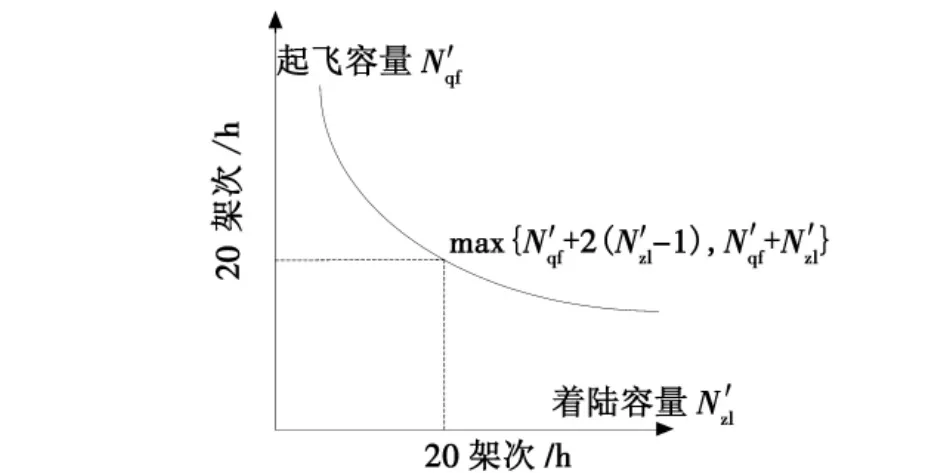
图1 跑道起降容量关系示意图Fig.1 The relation of runway taking off and landing capacity

因此，在该机场上，如果按演习任务，两个型号飞机在一天24 h内均连续运行，即准备起飞、起飞、执行任务、返航着陆、再次出动准备，受到飞机出动强度和机场保障能力影响，假设不同型号的飞机平均日出动强度为8，则在跑道满负荷服务情况下，进驻该机场的最大飞机数量为40×24/8=120架，且该数量满足最大可调配数。

5 结束语

机场容量是决定飞机可出动架次的关键因素，对飞机空中飞行时间产生了重要影响。本文运用排队论模型，计算出作战飞机起飞和着陆对机场容量的需求，并以机场容量为约束条件，建立了作战飞机调配需求模型，对作战飞机的数量进行调配。该模型的建立对战时装备指挥决策人员对作战飞机调配和补充有一定的参考作用。

［1］吴汉林，周根娜，柏林.做好多机种航材保障提高反空袭能力［J］.后勤科技装备，2000(3):55-56.

［2］中国人民解放军空军装备技术部编.空军航空工程辞典［M］.北京:中国科学技术出版社，1998.

［3］张最良，李长生.军事运筹学［M］.北京:军事科学出版社，1993.

［4］唐应辉，唐小我.排队论 －基础与分析技术［M］.北京:科学出版社，2006.

［5］王声.战时机场保障概论［M］.北京:空军后勤部机场管理部，2005.

［6］王莉莉，陈云翔，车飞.基于任务和战损的作战飞机调配保障需求模型［J］.电光与控制，2009，16(6):42-44.